POJ 1679 The Unique MST

 

 

关于次小生成树的构造：

 

在求最小生成树时，用数组Max[i][j]来表示MST中i到j最大边权。

求完后，直接枚举所有不在MST中的边，把它加入到MST中构成一棵新的树，且该树有环，此环是由刚加入的边(i,j)造成的，所以可以通过删除Max[i][j]即可得到新的一颗树，且所有的该类树中必有一棵为次小生成树。

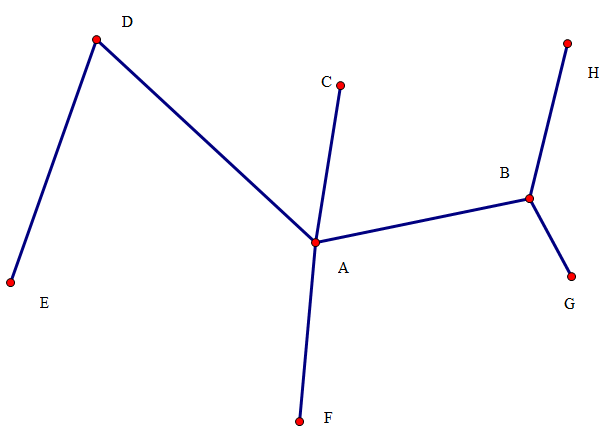
如图所示：

G,H不是MST上的边，通过加入边(G,H),得到一个环（B,H,G）,由于在计算最小生成树时已经计算出G,H之间最大边权为Max[G][H] = BH，所以通过删除BH即可得到一棵此时最小的生成树，然后更新答案即可。

实际上，我们知道MST的构造是具有贪心性质的，假如上图是一棵MST的话，那么必然有w(B,H) < w(G,H)。实际上w(B,H)是G->H的第二大边权，所以我们可以增加w(G,H)，然后删除w(B,H)得到的是权值和第二大的树，这时我们就可以通过枚举所有不在MST树中（!use[i][j]）的办法来生成次小生成树。

 

CODE：

 

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
using namespace std;

const int MAXN = 110;
const int INF = 0x3f3f3f3f;
int N, M;
int w[MAXN][MAXN] ,d[MAXN];
bool vis[MAXN], use[MAXN][MAXN];
int cnt ,fa[MAXN], Max[MAXN][MAXN] ;

void init()
{
    cnt = 0;
    memset(use, 0, sizeof(use));
    memset(vis, 0, sizeof(vis));
    memset(w, INF, sizeof(w));
    memset(Max, 0, sizeof(Max));
}

void Prim(int src)
{
    for(int i = 1; i <= N; i++) d[i] = (i == src)? 0:INF;
    for(int i = 1; i <= N; i++) fa[i] = i;
    for(int i = 1; i <= N; i++)
    {
        int m = INF, x ;
        for(int y = 1; y <= N; y++) if(!vis[y] && d[y] < m) m = d[x=y];
        for(int y = 1; y <= N; y++) if(vis[y])/*这是算法的关键，记录下vis[y]到k的路径中权值最大的值，用于替换处理*/
        {
            Max[x][y] = Max[y][x] = max(Max[y][fa[x]], d[x]);    //这里我出现了一个非常严重的错误，POJ竟然没报错！！
            //Max[x][y] = Max[y][x] = d[x]; 
        }
        vis[x] = 1;
        use[x][fa[x]] = use[fa[x]][x] = 1; //标记在MST树中 
        cnt += m;
        for(int y = 1; y <= N; y++)
        {
            if(!vis[y] && d[y] > w[x][y])
            {
                d[y] = w[x][y];
                fa[y] = x; //记录父亲节点 
             }
        }
    }
}

int smst() //second MST
{
    int Min = INF;
    for(int i = 1; i <= N; i++)
    {
        for(int j = i+1; j <= N; j++)
        {
            if(w[i][j] != INF && !use[i][j])
            {
                int res = cnt + w[i][j] - Max[i][j];
                Min = min(Min, res);
            }
        }
    }
    if(Min == cnt) return 0;
    return 1;
}


int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        init();
        scanf("%d%d", &N, &M);
        while(M--)
        {
            int u, v, cost;
            scanf("%d%d%d", &u, &v, &cost);
            if(w[u][v] > cost) //可能有重边 
            {
                w[u][v] = w[v][u] = cost;
            }
        }
        Prim(1);
        if(smst())
        {
            printf("%d\n", cnt);
        }
        else printf("Not Unique!\n");
    }
    return 0;
}

 

 CODE：

 

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
using namespace std;

const int MAXN = 110;
const int INF = 0x3f3f3f3f;
int n, m;
int w[MAXN][MAXN], d[MAXN];
bool vis[MAXN], use[MAXN][MAXN];
int cnt ,fa[MAXN], path[MAXN][MAXN];

void init()
{
    cnt = 0;
    memset(use, 0, sizeof(use));
    memset(vis, 0, sizeof(vis));
    memset(w, INF, sizeof(w));
    memset(path, 0, sizeof(path));
}

void Prim(int src)
{
    for(int i = 1; i <= n; i++) { d[i] = (i == src)?0:INF; fa[i] = i; }
    for(int i = 1; i <= n; i++)
    {
        int x, m = INF;
        for(int y = 1; y <= n; y++) if(!vis[y] && m > d[y]) m = d[x=y];
        for(int y = 1; y <= n; y++) if(vis[y]) //更新 
        {
            path[x][y] = path[y][x] = max(path[y][fa[x]], d[x]);
        }
        vis[x] = 1;
        use[x][fa[x]] = use[fa[x]][x] = 1;
        cnt += m;
        for(int y = 1; y <= n; y++) if(d[y] > w[x][y])
        {
            d[y] = w[x][y];
            fa[y] = x;
        }
    }
}

int smst()
{
    int Min = INF, res;
    for(int i = 1; i <= n; i++)
    {
        for(int j = i+1; j <= n; j++) if(w[i][j] != INF && !use[i][j]) //枚举 
        {
            res = cnt + w[i][j] - path[i][j];
            Min = min(Min, res);
        }
    }
    if(Min == cnt) return 0;
    return 1;
}


int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        init();
        scanf("%d%d", &n, &m);
        while(m--)
        {
            int u, v, cost;
            scanf("%d%d%d", &u, &v, &cost);
            if(w[u][v] > cost) //可能有重边 
            {
                w[u][v] = w[v][u] = cost;
            }
        }
        Prim(1);
        if(smst())
        {
            printf("%d\n", cnt);
        }
        else printf("Not Unique!\n");
    }
    return 0;
}