字典树模板
原理详见:https://www.cnblogs.com/TheRoadToTheGold/p/6290732.html
模板一:
输入字符串,查询是不是单词或者前缀
查询单词的时候,在插入时在最后一个节点的地方标记为单词,查询时返回最后节点是不是单词标记
1 const int maxn = 1e6 + 10; 2 int tree[maxn][26]; 3 //字典树tree[u][v]表示编号为u的节点的下一个字母为v连接的节点的编号 4 int idx(char c){ return c - 'a'; }//可以写成宏定义 5 int tot = 1;//根节点编号为1 6 bool is_word[maxn];//单词结束标记 7 void Insert(char s[], int u)//u表示根节点 8 //插入字符串s 9 { 10 for(int i = 0; s[i]; i++) 11 { 12 int c = idx(s[i]); 13 if(!tree[u][c]) 14 tree[u][c] = ++tot; 15 u = tree[u][c]; 16 } 17 //is_word [u] = true; //查询单词的时候需要标记最后一个节点的地方是单词 18 } 19 20 bool Find(char s[], int u) 21 //查询s是否是前缀 22 { 23 for(int i = 0; s[i]; i++) 24 { 25 int c = idx(s[i]); 26 if(!tree[u][c]) 27 return false; 28 u = tree[u][c]; 29 } 30 return true; 31 //return is_word[u]; //查询s是否是单词的时候,需要返回当前是不是单词结束标志 32 }
统计前缀出现的次数:
由于字典树中字母是边,节点是编号,统计前缀出现次数时,开一个sum数组表示该编号为终点的前缀出现次数,在每次加入一个字母的时候,总是在这条字母表示的边的后面那个节点加一。
比如下图,红色表示每个节点为终点的前缀出现的次数,每个字母表示边。
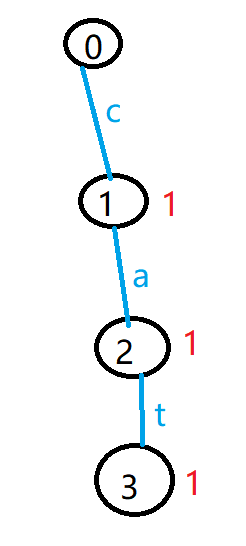
这里在每条边的后面那个节点上表示该前缀出现的次数。
如果在每条边的前面那个节点上表示该前缀出现的次数,会导致错误,因为根节点就不知道到底表示成什么字母出现的次数

查询c为前缀的数目的时候返回编号1的sum值
查询ca为前缀的数目的时候返回编号2的sum值
1 const int maxn = 1e6 + 10; 2 int tree[maxn][26]; 3 //字典树tree[u][v]表示编号为u的节点的下一个字母为v连接的节点的编号 4 int idx(char c){ return c - 'a'; }//可以写成宏定义 5 int tot = 1;//根节点编号为1 6 int sum[maxn];//标记以该节点结束的前缀出现次数 7 void Insert(char s[], int u)//u表示根节点 8 //插入字符串s 9 { 10 for(int i = 0; s[i]; i++) 11 { 12 int c = idx(s[i]); 13 if(!tree[u][c]) 14 tree[u][c] = ++tot; 15 sum[tree[u][c]]++; //前缀后面的那个节点数目加一 16 u = tree[u][c]; 17 } 18 } 19 20 int Find_sum(char s[], int u) 21 { 22 for(int i = 0; s[i]; i++) 23 { 24 int c = idx(s[i]); 25 if(!tree[u][c])return 0; 26 u = tree[u][c]; 27 } 28 return sum[u];//返回最后一个字母表示的边连接的后面那个节点,所记录的sum值 29 }
删除包含某前缀的所有单词
1 void Delete(char s[], int u)//删除所有包含该前缀的单词 2 { 3 int cnt = Find_sum(s, u); 4 if(cnt <= 0)return; 5 6 for(int i = 0; s[i]; i++)//前缀路径上全部删去cnt个单词 7 { 8 int c = idx(s[i]); 9 if(!tree[u][c])return; 10 sum[u] -= cnt; 11 u = tree[u][c]; 12 } 13 sum[u] = 0;//最末尾直接赋值成0 14 for(int i = 0; i < 26; i++)//最末尾的每个子节点全部清空 15 tree[u][i] = 0; 16 }
越努力,越幸运



