网络流（三）最大流最小割定理

传送门：

网络流（一）基础知识篇

网络流（二）最大流的增广路算法

网络流（三）最大流最小割定理

网络流（四）dinic算法

网络流（五）有上下限的最大流

网络流（六）最小费用最大流问题

转载：https://blog.csdn.net/w417950004/article/details/50538948

割(CUT)是网络中顶点的划分，它把网络中的所有顶点划分成两个顶点的集合源点S和汇点T。记为CUT(S,T)。

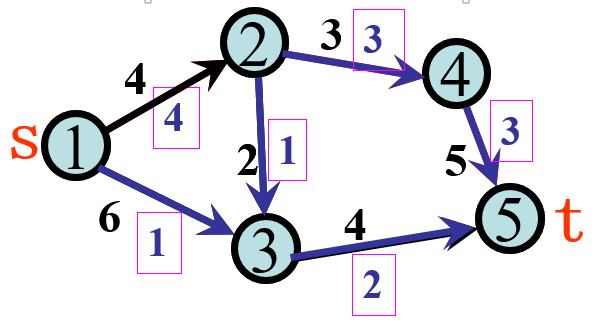
如下图：源点：s=1;汇点：t=5。框外是容量，框内是流量

 

 

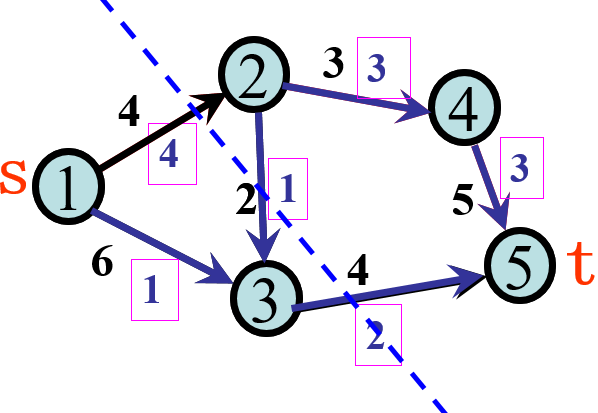
如下图是一个图的割。顶点集合S={1，2，3}和T={4，5}构成一个割。

           

如果一条弧的两个顶点分别属于顶点集S和T那么这条弧称为割CUT(S,T)的一条割边。  从S指向T的割边是正向割边，从T指向S的割边是逆向割边。如上图正向割边：

1->2;3->5      逆向割边：2->3。

割CUT(S,T)中所有正向割边的容量和称为割的容量。不同的个的容量不同。如上图割的容量为4+4=8；割的正向流量：4+2=6    逆向割的流量：1。

定理一：如果f是网络中的一个流，CUT（S,T）是任意一个割，那么流量f的值等于正向割边的流量与负向割边的流量之差。

推理提示：如果V既不是源点也不是汇点，那么：f({V},S∪T)-f(S∪T,{V})=0; 任何一个点，流入的与流出的量相等。

        结论：f= f(S,T)- f(T,S)<=f(S,T)<=割CUT（S,T）的容量 。 

推论1：如果f是网络中的一个流，CUT（S,T）是一个割，那么f的值不超过割CUT（S,T）的容量。

推论2：网络中的最大流不超过任何割的容量 

 

定理2： 在任何网络中，如果f是一个流，CUT（S,T）是一个割，且f的值等于割CUT（S,T）的容量，那么f是一个最大流，CUT（S,T）是一个最小割（容量最小的割）。

 

 

定理3：最大流最小割定量： 在任何的网络中，最大流的值等于最小割的容量。

结论1：最大流时，最小割cut（S，T）中，正向割边的流量=容量，逆向割边的流量为0。否则还可以增广。

结论2：在最小割中cut（S，T）中：

                         ① 源点s∈S。

                         ② 如果i∈S，结点j满足：有弧<i,j>,并且c[I,j]>f[I,j]  或者有弧<j,i>并且f[j,i]>0,那么j∈S。//否则不是最小割

                         即从s出发能找到的含有残留的点组成集合S。其余的点组成集合T。