网络流(二)最大流的增广路算法
传送门:
网络流(一)基础知识篇
网络流(二)最大流的增广路算法
网络流(三)最大流最小割定理
网络流(四)dinic算法
网络流(五)有上下限的最大流
网络流(六)最小费用最大流问题
转载:https://www.cnblogs.com/ZJUT-jiangnan/p/3632525.html
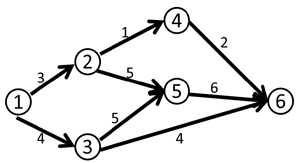
网络流的相关定义:
- 源点:有n个点,有m条有向边,有一个点很特殊,只出不进,叫做源点。
- 汇点:另一个点也很特殊,只进不出,叫做汇点。
- 容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].
通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最大的车流量。很显然的,流量<=容量。而对于每个不是源点和汇点的点来说,可以类比的想象成没有存储功能的货物的中转站,所有“进入”他们的流量和等于所有从他本身“出去”的流量。
- 最大流:把源点比作工厂的话,问题就是求从工厂最大可以发出多少货物,是不至于超过道路的容量限制,也就是,最大流。
求解思路:
首先,假如所有边上的流量都没有超过容量(不大于容量),那么就把这一组流量,或者说,这个流,称为一个可行流。
一个最简单的例子就是,零流,即所有的流量都是0的流。
- (1).我们就从这个零流开始考虑,假如有这么一条路,这条路从源点开始一直一段一段的连到了汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。
- (2).那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流,这是显然的。
- (3).这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路。我们不断地从起点开始寻找增广路,每次都对其进行增广,直到源点和汇点不连通,也就是找不到增广路为止。
- (4).当找不到增广路的时候,当前的流量就是最大流,这个结论非常重要。
补充:
- (1).寻找增广路的时候我们可以简单的从源点开始做BFS,并不断修改这条路上的delta 量,直到找到源点或者找不到增广路。
- (2).在程序实现的时候,我们通常只是用一个c 数组来记录容量,而不记录流量,当流量+delta 的时候,我们可以通过容量-delta 来实现,以方便程序的实现。
相关问题:
为什么要增加反向边?
在做增广路时可能会阻塞后面的增广路,或者说,做增广路本来是有个顺序才能找完最大流的。
但我们是任意找的,为了修正,就每次将流量加在了反向弧上,让后面的流能够进行自我调整。
举例:
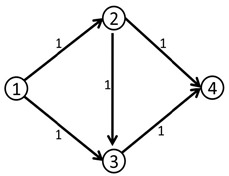
比如说下面这个网络流模型
我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。
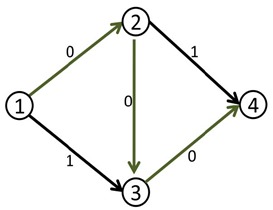
于是我们修改后得到了下面这个流。(图中的数字是容量)
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但是,
这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?
问题就在于我们没有给程序一个“后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。
那么如何解决这个问题呢?
我们利用一个叫做反向边的概念来解决这个问题。即每条边(i,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。
c[x,y]-=delta;c[y,x]+=delta;
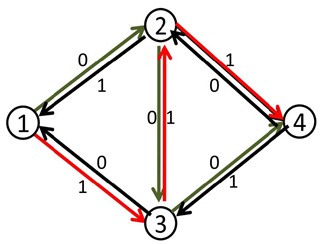
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下:这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。
那么,这么做为什么会是对的呢?
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给“退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。
如果这里没有2-4怎么办?
这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点
同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流。
下面是刘汝佳的模板,用水流会更容易理解
1 struct edge 2 { 3 int from, to, cap, flow;//分别是起点,终点,容量,流量 4 edge(int u, int v, int c, int f):from(u), to(v), cap(c), flow(f){} 5 }; 6 int n, m;//n为点数,m为边数 7 vector<edge>e;//保存所有边的信息 8 vector<int>G[maxn];//邻接表,G[i][j]保存节点i的第j条边在e数组里面的编号 9 int a[maxn];//每个点目前流经的水量 10 int p[maxn];//p[i]从原点s到终点t的节点i的前一条边的编号 11 12 void init(int n) 13 { 14 for(int i = 0; i <= n; i++)G[i].clear(); 15 e.clear(); 16 } 17 void addedge(int u, int v, int c) 18 { 19 e.push_back(edge(u, v, c, 0));//正向边 20 e.push_back(edge(v, u, 0, 0));//反向边,容量为0 21 m = e.size(); 22 G[u].push_back(m - 2); 23 G[v].push_back(m - 1); 24 } 25 int Maxflow(int s, int t)//起点为s,终点为t 26 { 27 int flow = 0; 28 for(;;) 29 { 30 memset(a, 0, sizeof(a));//从原点s开始放水,最初每个点的水量都为0 31 queue<int>Q;//BFS拓展队列 32 Q.push(s); 33 a[s] = INF;//原点的水设置成INF 34 while(!Q.empty()) 35 { 36 int x = Q.front();//取出目前水流到的节点 37 Q.pop(); 38 for(int i = 0; i < G[x].size(); i++)//所有邻接节点 39 { 40 edge& now = e[G[x][i]]; 41 if(!a[now.to] && now.cap > now.flow) 42 //a[i]为0表示i点还未流到 43 //now.cap > now.flow 说明这条路还没流满 44 //同时满足这两个条件,水流可以流过这条路 45 { 46 p[now.to] = G[x][i];//反向记录路径 47 a[now.to] = min(a[x], now.cap - now.flow); 48 //流到下一点的水量为上一点的水量或者路径上还可以流的最大流量,这两者取最小值 49 Q.push(now.to);//将下一个节点入队列 50 } 51 } 52 if(a[t])break;//如果已经流到了终点t,退出本次找增广路 53 } 54 if(!a[t])break;//如果所有路都已经试过,水不能流到终点,说明已经没有增广路,已经是最大流 55 for(int u = t; u != s; u = e[p[u]].from)//反向记录路径 56 { 57 e[p[u]].flow += a[t];//路径上所有正向边的流量增加流到终点的流量 58 e[p[u]^1].flow -= a[t];//路径上所有反向边的流量减少流到终点的流量 59 } 60 flow += a[t];//最大流加上本次流到终点的流量 61 } 62 return flow; 63 }