快速幂

引入：求a^b%c其中a、b数值很大，可能达到10¹⁸。

基础知识：

模运算：

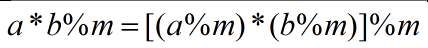
证明：

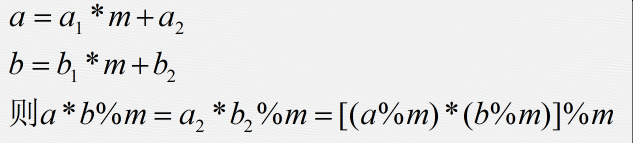
由上述可知a^b%m = （a%m）^b%m

快速幂：

对于任何一个整数的模幂运算
a^b%c
对于b我们可以拆成二进制的形式
b=b0+b1*2+b2*2^2+...+bn*2^n
这里我们的b0对应的是b二进制的第一位
那么我们的a^b运算就可以拆解成
a^b0*a^b1*2*...*a^(bn*2^n)
对于b来说，二进制位不是0就是1，那么对于bx为0的项我们的计算结果是1就不用考虑了，我们真正想要的其实是b的非0二进制位

那么假设除去了b的0的二进制位之后我们得到的式子是
a^(bx*2^x)*...*a(bn*2^n)
这里我们再应用我们一开始提到的公式，那么我们的a^b%c运算就可以转化为
(a^(bx*2^x)%c）*...*(a^(bn*2^n)%c)
这样的话，我们就很接近快速幂的本质了

以b=11为例，b=11=1011_（2），所以a^b = a^(2^0) * a^(2^1) * a ^ (2^3)；

下面给代码：

ll pow(ll a, ll b, ll m)
{
    ll ans = 1;
    a %= m;
    while(b)
    {
        if(b & 1)ans = (ans % m) * (a % m) % m;
        b /= 2;
        a = (a % m) * (a % m) % m;
    }
    ans %= m;
    return ans;
}

用上面的例子来模拟代码运行

b&1 = 1成立；所以ans *= a；这里就相当于ans = a^(2^0)

a *= a此时a为a^(2^1)

b/=2变成了5

b&1 = 1成立，ans *= a，此时ans = a^(2^0) * a^(2^1)

a *= a此时a为a^(2^2)

然后b/=2变成了2

b&1 = 1不成立

a *= a此时a为a^(2^3)

然后b/=2变成了1

b&1 = 1成立 ans*= a 此时ans =  a^(2^0) * a^(2^1) * a^(2^3)

a *= a此时a为a^(2^4)

b/=2变成0，跳出循环

上述就是通过二进制的方式来操作快速幂。

 

当mod过大的时候，需要在快速幂的基础上加上快速加法，防止乘法溢出

计算a*b%m可以（a % m）*（b%m）%m

但是当m很大的时候，还是会溢出。可以用快速加法防止溢出

ll mul(ll a, ll b, ll m)
//求a*b%m
{
    ll ans = 0;
    a %= m;
    while(b)
    {
        if(b & 1)ans = (ans + a) % m;
        b /= 2;
        a = (a + a) % m;
    }
    return ans;
}
ll pow(ll a, ll b, ll m)
{
    ll ans = 1;
    a %= m;
    while(b)
    {
        if(b & 1)ans = mul(a, ans, m);
        b /= 2;
        a = mul(a, a, m);
    }
    ans %= m;
    return ans;
}