单源最短路径---Bellman-Ford算法
传送门:
Bellman-Ford
1.Dijkstra算法的局限性
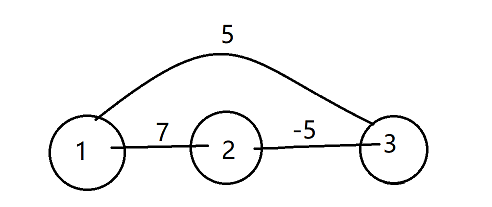
像上图,如果用dijkstra算法的话就会出错,因为如果从1开始,第一步dist[2] = 7, dist[3] = 5;在其中找出最小的边是dist[3] = 5;然后更新dist[2] = 0,最终得到dist[2] = 0,dist[3] = 5,而实际上dist[3] = 2;所以如果图中含有负权值,dijkstra失效
2.Bellman-Ford算法思想
适用前提:没有负环(或称为负权值回路),因为有负环的话距离为负无穷。
构造一个最短路径长度数组序列dist1[u] dist2[u]...distn-1[u],其中:
dist1[u]为从源点v0出发到终点u的只经过一条边的最短路径长度,并有dist1[u] = Edge[v0][u]
dist2[u]为从源点v0出发最多经过不构成负权值回路的两条边到终点u的最短路径长度
dist3[u]为从源点v0出发最多经过不构成负权值回路的三条边到终点u的最短路径长度
................
distn-1[u]为从源点v0出发最多经过不构成负权值回路的n-1条边到终点u的最短路径长度
算法最终目的是计算出distn-1[u],即为源点到顶点u的最短路径长度
初始:dist1[u] = Edge[v0][u]
递推:distk[u] = min(distk-1[u], min{distk-1[j] + Edge[j][u]})(松弛操作,迭代n-2次)
3.本质思想:
在从distk-1[u]递推到distk[u]的时候,Bellman-Ford算法的本质是对每条边<u, v>进行判断:设边<u, v>的权值为w(u, v),如果边<u, v>的引入会使得distk-1[v]的值再减小,就要修改distk-1[v],即:如果distk-1[u] + w(u, v) < distk-1[v],,那么distk[v] = distk-1[u] + w(u, v),这个称为一次松弛
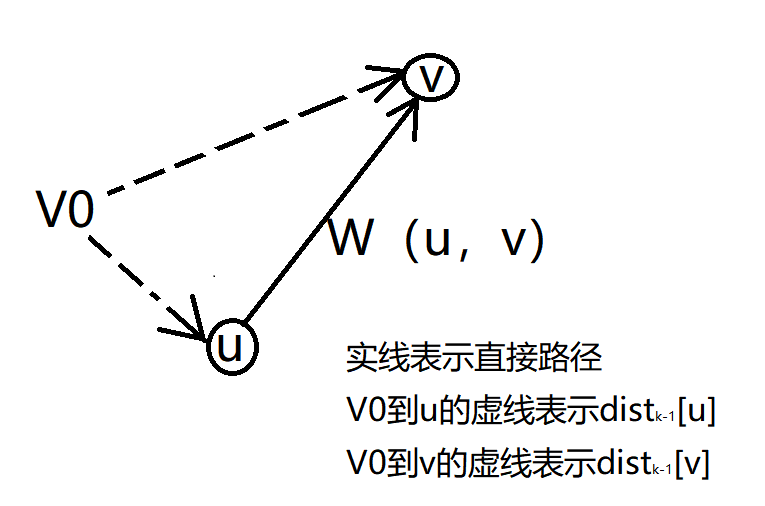
所以递推公式可改为:
初始:dist0[u] = INF dist0[v0] = 0(v0是源点)
递推:对于每条边(u, v) distk[v] = min(distk-1[v], distk-1[u] + w(u, v))(松弛操作,迭代n-1次)
如果迭代n-1次后,再次迭代,如果此时还有dist会更新,说明存在负环。
无负环的时候,迭代更新次数最多为n-1次,所以设置一个更新变量可以在不更新的时候直接跳出循环
拓展:
Bellman-Ford算法还能用来求最长路或者判断正环,思路是dist数组含义是从原点出发到其他每个顶点的最长路径的长度,初始时,各个顶点dist为0,在从distk-1[u]递推到distk[u]的时候,Bellman-Ford算法的本质是对每条边<u, v>进行判断:设边<u, v>的权值为w(u, v),如果边<u, v>的引入会使得distk-1[v]的值再增加,就要修改distk-1[v],即:如果distk-1[u] + w(u, v) > distk-1[v],,那么distk[v] = distk-1[u] + w(u, v)。例题:POJ-1860
4.代码实现:时间复杂度O(nm)(n为点数,m为边数)
输入:
7 10
0 1 6
0 2 5
0 3 5
1 4 -1
2 1 -2
2 4 1
3 2 -2
3 5 -1
4 6 3
5 6 3
输出:
从0到1距离是: 1 0->3->2->1
从0到2距离是: 3 0->3->2
从0到3距离是: 5 0->3
从0到4距离是: 0 0->3->2->1->4
从0到5距离是: 4 0->3->5
从0到6距离是: 3 0->3->2->1->4->6
不存在负环
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #include<queue> 7 #include<stack> 8 #include<map> 9 #include<sstream> 10 using namespace std; 11 typedef long long ll; 12 const int maxn = 1000 + 10; 13 const int INF = 1 << 25; 14 int T, n, m, cases; 15 struct edge 16 { 17 int u, v, w; 18 }; 19 edge a[maxn]; 20 int path[maxn], d[maxn]; 21 bool Bellman(int v0) 22 { 23 for(int i = 0; i < n; i++)d[i] = INF, path[i] = -1; 24 d[v0] = 0; 25 for(int i = 0; i < n; i++)//迭代n次,如果第n次还在更新,说明有负环 26 { 27 bool update = 0; 28 for(int j = 0; j < m; j++) 29 { 30 int x = a[j].u, y = a[j].v; 31 //cout<<x<<" "<<y<<" "<<a[j].w<<endl; 32 if(d[x] < INF && d[x] + a[j].w < d[y]) 33 { 34 d[y] = d[x] + a[j].w; 35 path[y] = x; 36 update = 1; 37 if(i == n - 1)//说明第n次还在更新 38 { 39 return true;//返回真,真的存在负环 40 } 41 } 42 } 43 if(!update)break;//如果没更新了,说明已经松弛完毕 44 } 45 for(int i = 0; i < n; i++) 46 { 47 if(i == v0)continue; 48 printf("从%d到%d距离是:%2d ", v0, i, d[i]); 49 stack<int>q; 50 int x = i; 51 while(path[x] != -1) 52 { 53 q.push(x); 54 x = path[x]; 55 } 56 cout<<v0; 57 while(!q.empty()) 58 { 59 cout<<"->"<<q.top(); 60 q.pop(); 61 } 62 cout<<endl; 63 } 64 return false; 65 } 66 int main() 67 { 68 cin >> n >> m; 69 for(int i = 0; i < m; i++)cin >> a[i].u >> a[i].v >> a[i].w; 70 if(Bellman(0))cout<<"存在负环"<<endl; 71 else cout<<"不存在负环"<<endl; 72 return 0; 73 }



