例题3-2,蛇形填数,解题报告
作者:fzd19zx@gmail.com 2011年2月1日 21:09:28
本题,是《算法竞赛入门经典》(刘汝佳)的一道例题。(P35,例题3-2)
题目描述如下:(我改进了一点点,使之叙述得更加严密。)
问题描述:
在n*n的方阵里填入1,2,3,...,n*n,要求填成蛇形。
1<=n<=19
由于在标准的命令行界面下,每个屏幕大约只有25行,所以不必让n具有特别大的值。
当然如果你采用重定向技术,把结果输出到文件中,那么就没有这种局限性了。
假设用户输入的数据都是合法的。
输入:1个整数n
输出:蛇形填数的结果;每个数字占2个字符的位置,各数字之间用1个空格隔开
例如:
4
10 11 12 1
9 16 13 2
8 15 14 3
7 6 5 4
=============================================
本题,利用一个二维数组来存储和输出计算的结果,看起来是一个“很自然”的解法。
我的解题策略描述如下:
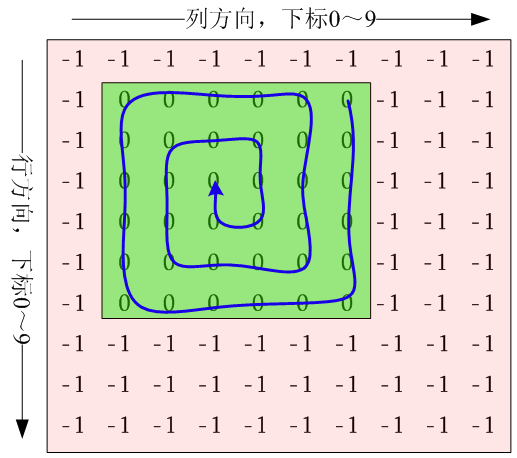
把整个数组想象成一幅地图。有一个机器人从地图的左上角开始,按照蛇形填数的方案行走。每走一步,机器人就会在当前位置填上自己的当前步数。如此,当机器人走了n*n步之后,蛇形填数即被完成。
显然,可以用一个二维数组来表示这幅地图。同时,二维数组的2个下标分别可以机器人所在地位置。
看起来,代码片段是这样的:
0001 # define MAX (10) /*地图的行/列上限*/ 0002 # define BRICK (-1) /*砖块:表示机器人不能走到该位置*/ 0003 # define BLANK (0) /*空白:表示机器人可以走到该位置*/ 0004 int map[MAX][MAX], /*地图*/ 0005 n, /*机器人一共要走n*n步*/ 0006 i,j; 0007 /*初始化地图:先全部铺上砖块*/ 0008 for (i=0; i<=MAX-1; i=i+1) { 0009 for (j=0; j<=MAX-1; j=j+1) { 0010 map[i][j]=BRICK; 0011 } 0012 } 0013 /*初始化地图:再挖出需要蛇形填数的区域*/ 0014 scanf("%d",&n); 0015 for (i=1; i<=n; i=i+1) { 0016 for (j=1; j<=n; j=j+1) { 0017 map[i][j]=BLANK; 0018 } 0019 }
例如上面的代码,给出的地图看起来像是这样的:
0001 /*打印机器人走出的地图*/ 0002 for (i=0; i<MAX; i=i+1) { 0003 for (j=0; j<MAX; j=j+1) { 0004 printf("%3d ",map[i][j]); /*每个输出数据占3个字符的宽度*/ 0005 } 0006 printf("\n"); /*每行的结尾打印一个回车换行标记*/ 0007 }
绿色的区域,就是我们要让机器人在其中按照“蛇形填数”的要求行走的区域。
蓝色的线条和箭头,意指机器人行走的路线和方向。
粉色的区域,是不可到达的位置。我们用砖块(BRICK)填满这些地方。
由上图可见,我们总是可以用二维数组的2个下标(整数)来表示机器人的当前位置。比如,机器人一开始的位置位于map[1][6];该处的值应当为1,意指机器人在这个位置落下的是第1步。
策略的关键是:如何在已知机器人当前位置的情况下,判定出机器人下一步应该要走到哪个位置?
为此,我采用了如下的判定策略表:
========================================================
当前可行动方向 | 下一步方向
========================================================
只能向左 | 向左
只能向右 | 向右
只能向上 | 向上
只能向下 | 向下
向左或向下 | 向下
向左或向上 | 向左
向右或向上 | 向上
向右或向下 | 向右
========================================================
一旦根据上述“判定策略表”做出了“下一步方向”,就应当“立即行动”,不能再看“判定策略表”中的其他项。举例说明:如果机器人采用了“只能向右,则向右”这一策略,那么就应当立刻走出这一步;而不应当继续其他的行动策略。关于这点的详细说明,请看源代码。
总而言之,当机器人面临着“下一步往哪儿走”的选择时,就可以根据上面的“判定策略表”作出抉择。而据此表所作出的选择,确保了机器人总是能沿着“蛇形填数”的方向走下去。
几个细节的说明:
1. # define MAX (10) /*地图的行/列上限*/ 限定了地图的大小。
2. # define BRICK (-1) /*砖块:表示机器人不能走到该位置*/ 事实上,如果map中某个位置的元素值只要不是BLANK(空白),机器人就不能走到那个位置。初始化时,将其值设定为BRICK(-1)是为了判断地图边界的时候比较方便。
3. 地图的最上方1行和最左端1列,都是没有使用的空间。我在里面填入BRICK,这样处理,会比较方便地判定机器人是否走到了地图的边界。
程序的源代码,在这里:
最后,我给出整个程序的控制流程图如下:
(说实话,这个流程图挺复杂的,看起来有点儿恶心。以后我们学会了函数,这个代码写起来,就会好看多了。)
小结:
1. 合适的数据表达形式(数据结构)是解决问题的关键。比如在这里,利用二维数组来表达地图,是“很自然”的解法。
2. 合理的解题策略,往往不止一个。比如书中的解题策略当然也是正确的。但我却很难理解其中的逻辑(悟性较差)。寻找自己所擅长理解的逻辑,也正是提高自己看问题水平的一个重要方面。
各位同学,如果你觉得你已经看懂了上述内容;那么,
请思考下面2个问题:
- 我的解题方案有什么不妥:在逻辑上有否漏洞?在代码上有否错误?你可否进一步提高代码的可读性或是效率?
- 本题中“蛇形”是顺时针的;你可否给出一个“逆时针方向的蛇形填数”?把你的代码贴到群里面。
谢谢观赏!
==========================================================
完整的源代码如下:
0001 /* 0002 例题3-2,蛇形填数.c 0003 20:49 2011年2月1日 0004 问题描述: 0005 在n*n的方阵里填入1,2,3,...,n*n,要求填成蛇形。 0006 1<=n<=19 0007 由于在标准的命令行界面下,每个屏幕大约只有25行,所以不必让n具有特别大的值。 0008 当然如果你采用重定向技术,把结果输出到文件中,那么就没有这种局限性了。 0009 假设用户输入的数据都是合法的。 0010 输入:1个整数n 0011 输出:蛇形填数的结果;每个数字占3个字符的位置,各数字之间用1个空格隔开 0012 例如: 0013 4 0014 10 11 12 1 0015 9 16 13 2 0016 8 15 14 3 0017 7 6 5 4 0018 解题策略:(详见“例题3-2,蛇形填数,解题报告.pdf”) 0019 把整个数组想象成一幅地图。有一个机器人从地图的左上角开始,按照蛇形填数的方案行走。每走一步,机器人就会在当前位置 0020 填上自己的当前步数。如此,当机器人走了n*n步之后,蛇形填数即被完成。 0021 显然,可以用一个二维数组来表示这幅地图。同时,二维数组的2个下标分别可以机器人所在地位置。 0022 所以,我们总是可以用二维数组的2个下标(整数)来表示机器人的当前位置。 0023 而该策略的关键是:如何在已知机器人当前位置的情况下,判定出机器人下一步应该要走到哪个位置? 0024 为此,我采用了如下的判定策略表: 0025 ======================================================== 0026 当前可行动方向 | 下一步方向 0027 ======================================================== 0028 只能向左 | 向左 0029 只能向右 | 向右 0030 只能向上 | 向上 0031 只能向下 | 向下 0032 向左或向下 | 向下 0033 向左或向上 | 向左 0034 向右或向上 | 向上 0035 向右或向下 | 向右 0036 ======================================================== 0037 一旦根据上述“判定策略表”做出了“下一步方向”,就应当“立即行动”,不能再看“判定策略表”中的其他项。 0038 关于这点,请看源代码。 0039 当机器人面临着“下一步往哪儿走”的选择时,就可以根据上面的“判定策略表”作出抉择。而据此表所作出的选择,确保了机器人 0040 总是沿着“蛇形填数”的方向走下去。 0041 */ 0042 # include "stdio.h" 0043 # define MAX (100) /*地图的行/列上限*/ 0044 # define BRICK (-1) /*砖块:表示机器人不能走到该位置*/ 0045 # define BLANK (0) /*空白:表示机器人可以走到该位置*/ 0046 int main() { 0047 int map[MAX][MAX], /*地图*/ 0048 robotX=1,robotY, /*机器人的位置*/ 0049 n, /*机器人一共要走n*n步*/ 0050 i,j, 0051 step=0; /*当前步数*/ 0052 0053 /*初始化地图:先全部铺上砖块*/ 0054 for (i=0; i<=MAX-1; i=i+1) { 0055 for (j=0; j<=MAX-1; j=j+1) { 0056 map[i][j]=BRICK; 0057 } 0058 } 0059 /*初始化地图:再挖出需要蛇形填数的区域*/ 0060 scanf("%d",&n); 0061 for (i=1; i<=n; i=i+1) { 0062 for (j=1; j<=n; j=j+1) { 0063 map[i][j]=BLANK; 0064 } 0065 } 0066 0067 /*初始化机器人的位置坐标*/ 0068 robotY=n; 0069 step=1; /*机器人走出第一步*/ 0070 map[robotX][robotY]=step; 0071 0072 /*机器人根据行动策略表,决定自己的下一步行动方向*/ 0073 step=step+1; 0074 while (step<=n*n) { 0075 /*只能向上,则向上*/ 0076 if (map[robotX-1][robotY]==BLANK && 0077 map[robotX+1][robotY]!=BLANK && 0078 map[robotX][robotY-1]!=BLANK && 0079 map[robotX][robotY+1]!=BLANK) { 0080 robotX=robotX-1; 0081 } 0082 else 0083 /*只能向下,则向下*/ 0084 if (map[robotX-1][robotY]!=BLANK && 0085 map[robotX+1][robotY]==BLANK && 0086 map[robotX][robotY-1]!=BLANK && 0087 map[robotX][robotY+1]!=BLANK) { 0088 robotX=robotX+1; 0089 } 0090 else 0091 /*只能向左,则向左*/ 0092 if (map[robotX-1][robotY]!=BLANK && 0093 map[robotX+1][robotY]!=BLANK && 0094 map[robotX][robotY-1]==BLANK && 0095 map[robotX][robotY+1]!=BLANK) { 0096 robotY=robotY-1; 0097 } 0098 else 0099 /*只能向右,则向右*/ 0100 if (map[robotX-1][robotY]!=BLANK && 0101 map[robotX+1][robotY]!=BLANK && 0102 map[robotX][robotY-1]!=BLANK && 0103 map[robotX][robotY+1]==BLANK) { 0104 robotY=robotY+1; 0105 } 0106 else 0107 /*向左或向下,则向下*/ 0108 if (map[robotX+1][robotY]==BLANK && map[robotX][robotY-1]==BLANK) { 0109 robotX=robotX+1; 0110 } 0111 else 0112 /*向左或向上,则向左*/ 0113 if (map[robotX-1][robotY]==BLANK && map[robotX][robotY-1]==BLANK) { 0114 robotY=robotY-1; 0115 } 0116 else 0117 /*向右或向上,则向上*/ 0118 if (map[robotX-1][robotY]==BLANK && map[robotX][robotY+1]==BLANK) { 0119 robotX=robotX-1; 0120 } 0121 else 0122 /*向右或向下,则向右*/ 0123 if (map[robotX+1][robotY]==BLANK && map[robotX][robotY+1]==BLANK) { 0124 robotY=robotY+1; 0125 } 0126 map[robotX][robotY]=step; 0127 step=step+1; 0128 } 0129 0130 /*打印机器人走出的地图*/ 0131 for (i=1; i<=n; i=i+1) { 0132 for (j=1; j<=n; j=j+1) { 0133 printf("%3d ",map[i][j]); /*每个输出数据占3个字符的宽度*/ 0134 } 0135 printf("\n"); /*每行的结尾打印一个回车换行标记*/ 0136 } 0137 return 0; 0138 }