算法导论中的四种基本排序

算法导论中常见的四种排序

                                                        by方阳

版权声明：本文为博主原创文章，转载请指明转载地址

http://www.cnblogs.com/fydeblog/p/7067382.html 

1. 前言

好久没写博客了，今天来一篇最近开始看的算法导论，这篇博客主要介绍插入排序，归并排序，堆排序和快速排序的原理，性能分析以及程序实现！废话不多说，let's go!

 

2. 原理解析

 

2.1 插入排序

参考下面的图片，再想想我们平时玩扑克牌，它的基本思路就清晰多了，假设待排序的记录存放在数组R[1..n]中。初始时，R[1]自成1个有序区，无序区为R[2..n]。从i=2起直至i=n为止，依次将R[i]插入当前的有序区R[1..i-1]中，生成含n个记录的有序区。

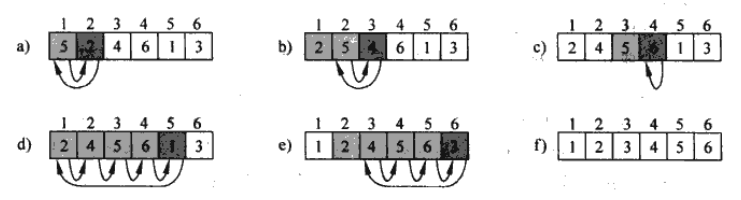
2.2 归并排序

参考下面的图片（从pdf上截的，有点歪），可以看出是将原数组进行分解，然后排序，在进行合并，归并排序是分治（Divide and conquer）策略的一个很好的例子，将复杂的问题分成许多小问题，分开解决，然后合并。

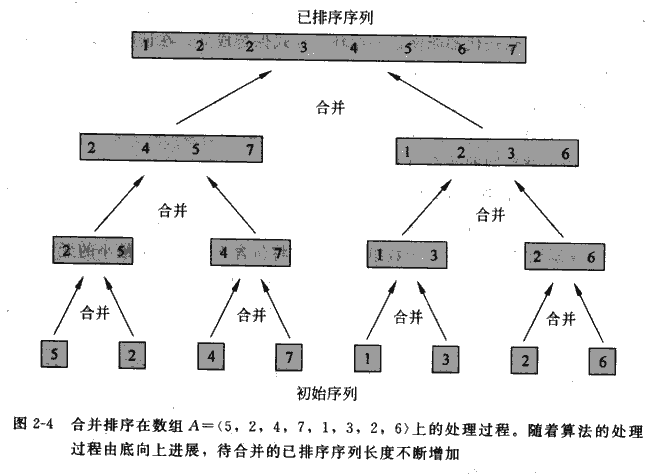
2.3 堆排序

堆排序涉及到的知识比较多，它主要分为三部分：MAX-HESPIFY，BUILD-MAX-HEAP 和 HEAPSORT

MAX-HESPIFY：维持最大堆的性质。

BUILD-MAX-HEAP：将无序的数据数组构造成一个最大堆。

HEAPSORT：对一个数组进行原址排序。

这里面涉及蛮多知识的，下面分别介绍一下！

最大堆的定义：在最大堆中，最大堆特性是指除了根以外的每个结点i，有A[PARENT(i)] >= A[i]。这样，堆的最大元素就存放在根结点中。

那下面的图片来说，就是序号1为根结点（也叫父结点），要大于序号2和3的元素（2,3也叫子类结点，左子结点和右子结点），其他结点类似按照这个来推

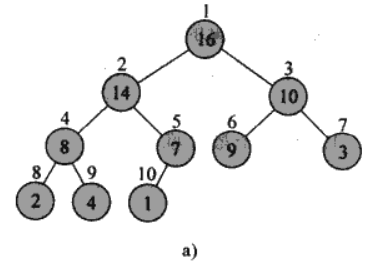
原址排序的定义：在排序输入数组时，只有常数个元素被存放到数组以外的空间中去。就是说不需要花数组那样大的空间来缓存数据，大部分排序都在数组内部进行！

MAX-HESPIFY（过程见下图，详细看代码）

 

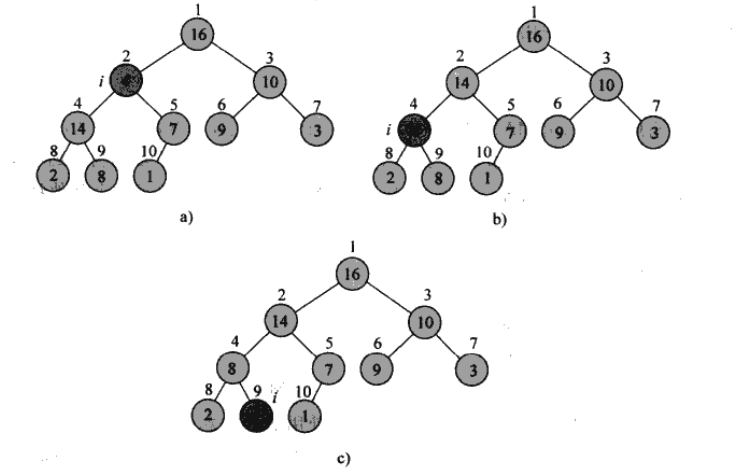
BUILD-MAX-HEAP（过程见下图，详细看代码）

 

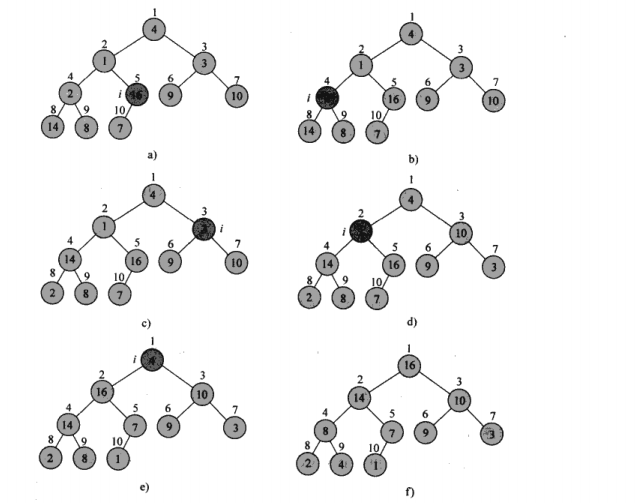
HEAPSORT（过程见下图，详细看代码）

 

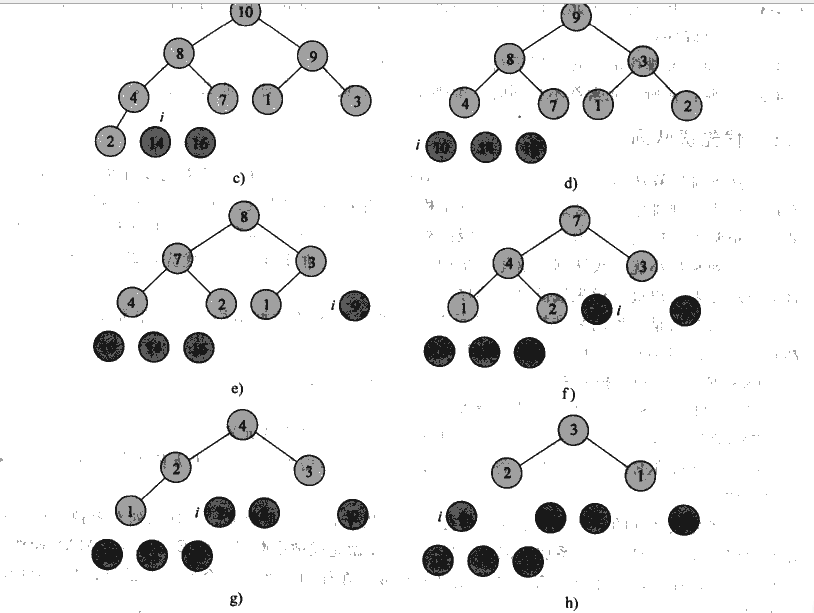
2.4 快速排序

 

快速排序使用分治策略来把一个数组分为两个子数组。

 

步骤为：

 

1. 从数组中挑出一個元素，称为 "基准"（pivot），
2. 重新排序数组，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分割之后，该基准是它的最后位置。这个称之为分割（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数组和大于基准值元素的子数组排序。

 如下图所示

 

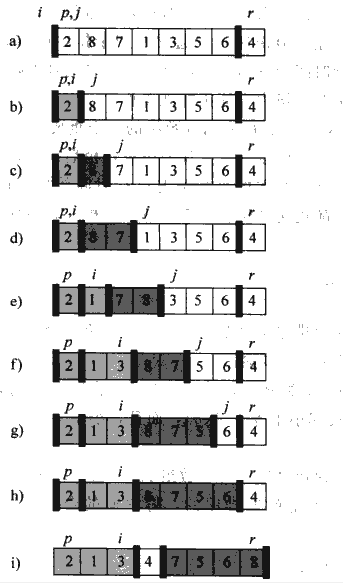
3.性能分析

3.1 运行时间

从图可以看出，在n很大时，归并排序和堆排序（它们接近最优）运行时间上比插入排序和快速排序，n值小时，插入和快排较快。实际应用中，快排用的较多，它一般快于堆排序。

归并排序和堆排序都是以二叉树形式，它的高度是lgn，每一层都要进行n次比较，所以最后最坏结果都是nlgn，而插入排序最坏的情况是每一个都要去比较，即n的平方，快排最坏的情况是分组一边0个元素，另一边是n-1，平均情况还是类似归并排序，也是分治法的最优情况，nlgn。

3.2 存储空间

插入排序和快速排序是原址排序算法，归并排序和堆排序不是，所以插入排序和快速排序占用空间小，更节省内存。

4. 程序实现

4.1. main.cpp

 

#include <iostream>
#include "fy_sort.h"
using namespace std;
 

int main()
{ 
  fy_sort sort1; 
  int num;
  int a[30],b[30],c[30],d[30];
  cout<<"please enter the number of input elements: "<<endl;
  cin >>  num;
  cout << "Input the elements:\n";
  for(int i=0;i<num;i++)
  {
      cin>>a[i];
      b[i]=a[i];
      c[i]=a[i];
      d[i]=a[i];
  }
  cout << "insert_sort:\n";
  sort1.insert_sort(a,num);//插入排序
  cout << "merge_sort:\n";
  sort1.merge_sort(b,0,num-1);//归并排序
  sort1.display(b,num);
  cout << "heap_sort:\n";
  sort1.heap_sort(c,num);//堆排序
  cout << "quick_sort:\n";
  sort1.quick_sort(d,0,num-1);//快速排序
  sort1.display(d,num);

  return 0;
}

4.2  fy_sort.h

 

#pragma once

#ifndef FY_SORT_H
#define FY_SORT_H

class fy_sort //排序类
{
private:
    
    void swap (int& n, int& m);                 //交换函数
    void merge(int a[],int p,int q,int r);      //归并排序函数
    inline int left  (int i) {return 2 * i + 1;}//内联函数，用于堆排序的左手序号  
    inline int right (int i){return 2 *(i + 1);}//内联函数，用于堆排序的右手序号  
    void max_heapify (int a[], int i);          //最大堆排序中的核心，维护最大堆的性质，即父类节点大于子类节点
    void build_max_heap (int a[], int n);       //建造最大堆，调用n/2次max_heapify,将无序的数组构造成最大堆
    int Partition(int a[], int beg, int end);   //快排的核心，即分割，将大于数组最后一个元素的元素移到右边，小于的移到左边

public:

   void display(const int a[],int k);        //显示函数
   void insert_sort(int a[],int n);          //插入排序
   void quick_sort(int a[],int beg, int end);//快速排序（递归调用）
   void merge_sort(int a[],int p,int r);     //归并排序（递归调用）
   void heap_sort(int a[],int n);            //堆排序
   
};

#endif

4.3 fy_sort.cpp

 

 

#include "fy_sort.h"
#include<iostream>

using namespace std;

int heap_size; 
//显示函数
void fy_sort::display(const int a[],int k) 
{
    for(int i=0;i<k;i++)
       cout<<a[i]<<" ";
       cout<<endl;
}
//交换函数
void fy_sort::swap (int& n, int& m)  
{  
    int temp;  
    temp = n;  
    n = m;  
    m = temp;  
} 

void fy_sort::insert_sort(int a[],int k)//插入排序
{
     int key;
     for (int i=1;i<k;i++)
     {
      key=a[i]; //先将要比较的元素暂存，后面要替换
      int j=i-1;
      //循环实现的功能找到比a[i]大的前面元素（序号小的），找到替换，无则不变
        while((j>-1)&&(key<a[j])) 
        {
          a[j+1]=a[j];
          j--;
        }
      a[j+1]=key;
     }
     display(a,k);    
}

void fy_sort::merge_sort(int a[],int p,int r) //归并排序
{
    if(p<r)
    {
        int q=(p+r)/2;     //以q值为划分区间，将数组划分成两个小数组
        merge_sort(a,p,q); //小数组再划分，递归调用，直到剩下一个
        merge_sort(a,q+1,r);//小数组再划分，递归调用，直到剩下一个
        merge(a,p,q,r);     //将分解后的最小数组，进行排序和合并
    }
    
}


void fy_sort::merge(int a[],int p,int q,int r)
{
    int n1 = q-p+1;  
    int n2 = r-q;  
    //生成两个新空间，存划分后的数组
    int *L = new int[n1+1];  
    int *R = new int[n2+1];  
    int i, j, k;  
    //将大数组的值赋给两个小数组      
    for (i=0; i<n1; i++){  
        L[i] = a[p+i];  
    }  
    for (j=0; j<n2; j++){  
        R[j] = a[q+j+1];  
    }
    //确定边界
    L[n1] = 10000000;  
    R[n2] = 10000000;  
    //按位比较，在合并成大数组  
    for (i=0, j=0, k=p; k<=r; k++)  
    {  
        if (L[i]<=R[j])  
        {  
            a[k] = L[i];  
            i++;  
        }else{  
            a[k] = R[j];  
            j++;  
        }  
    }  
    //释放空间  
    delete []L;  
    delete []R;  
}

void fy_sort::max_heapify (int a[], int i)  
{   
    //左手和右手的序号
    int l = left(i);  
    int r = right(i);
    //largest存储父节点和子节点中最大的数
    int largest;  
    //子类左结点与父节点比较，将其中大的赋给largest
    if ((l < heap_size) && a[l] > a[i])  
        largest = l;  
    else  
        largest = i;  
   //子类左结点与largest比较，将其中大的赋给largest
    if ((r < heap_size) && a[r] > a[largest])  
        largest = r;  
   //若根节点变化，会导致下面分支的最大堆性质可能变化，这里对下面进行重新分堆
    if (largest != i)  
    {  
        swap (a[largest], a[i]);  
        max_heapify (a, largest);  
    }  
}  

void fy_sort::build_max_heap (int a[], int n)  
{  
    heap_size=n; 
    //记住一点，最大堆是以由底向上分堆
    for (int i = (n - 1) / 2; i >= 0; i--)  
        max_heapify (a, i);  
}  

void fy_sort::heap_sort (int a[], int n)  
{  
    build_max_heap (a, n);
    //实现的是原址排序，将最大堆转化成从小到大的数组
    //原理是将最大堆的根节点换成最大堆最末尾的数，然后再进行最大堆
    //直到只剩下一个节点，即为最小值
    for (int i = n - 1; i >= 1; i--)  
    {  
        swap (a[i], a[0]);  
        heap_size--;  
        max_heapify (a, 0);  
    }  
    display(a,n);
} 
//快速排序的核心，也跟堆排序一样，是原址排序
int fy_sort::Partition(int a[], int beg, int end)
{
    int sentinel = a[end];
    int i = beg-1;
    //这个循环以最后一个为基准，小于a[end]的放到左边
    //大于a[end]放到右边
    for(int j=beg; j<=end-1; ++j)
    {
        if(a[j] <= sentinel)
        {
            i++;
            swap(a[i], a[j]);
        }
    }
    swap(a[i+1], a[end]);
 
    return i+1;
}

void fy_sort::quick_sort(int a[], int beg, int end)
{
    if(beg < end)
    {
        int pivot = Partition(a, beg, end);
        //后边这两个是对一部分划分的左右部分在进行快排
        quick_sort(a, beg, pivot-1);
        quick_sort(a, pivot+1, end);
    }
    
}

 

5.运行结果

 

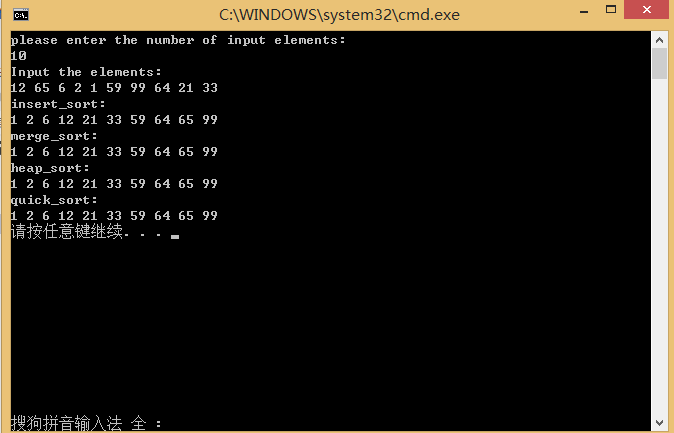
6.结束语

建议大家去看算法导论，里面讲的非常细，就是太厚了，容易看不下去！（笑哭）挑重点看吧，下次见！

这里再分享两位网友的笔记，写得很好！

Tanky Woo：  《算法导论》学习总结—【目录】

Adoo          :   《算法导论》笔记汇总