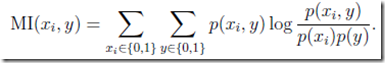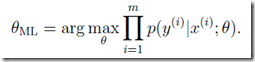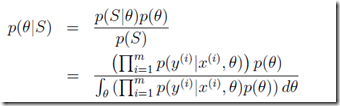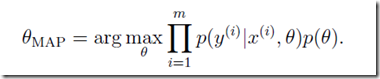Andrew Ng机器学习公开课笔记 -- Regularization and Model Selection

网易公开课，第10,11课
notes，http://cs229.stanford.edu/notes/cs229-notes5.pdf

 

Model Selection

首先需要解决的问题是，模型选择问题，如何来平衡bais和variance来自动选择模型？比如对于多项式分类，如何决定阶数k，对于locally weighted regression如何决定窗口大小，对于SVM如何决定参数C
For instance, we might be using a polynomial regression model , and wish to decide if k should be
0, 1, . . . , or 10.  Alternatively, suppose we want to automatically choose the bandwidth parameter τ for locally weighted regression, or the parameter C for our ℓ1-regularized SVM.

 

Cross validation

最典型的就是交叉验证，有3种方法，

hold-out cross validation (also called simple cross validation)
用70%的数据作为训练集，用30%数据作为测试集，找出训练误差最小的h（7:3是比较典型的比例）
这个方法的问题是，我们浪费了30%的数据，即使你在选定model后，拿整个数据集再做一遍训练，也无法改变你只用了70%来选择最优模型的事实
尤其对于一些领域，数据集的收集的代价是很高的，就不太合适

k-fold cross validation，通常k=10
把数据集随机分为k份，用k-1份来训练，用剩下的那份来测试，这样的过程可以进行k次（不同的组合）
最终选取平均测试误差最小的h
这个的问题，显然是计算量比较大

leave-one-out cross validation
k-fold的特例，k=m，即k等于样本数，一份就是一个样本
适用于样本非常少的情况

 

Feature Selection

One special and important case of model selection is called feature selection.
对于比如文本分类问题，垃圾邮件分类，会有很大量的features，但其实只有其中一小部分和分类问题相关，比如很多stop word，a，the，都和分类不相关，而buy，shop等比较相关的只是一小部分，所以我们需要减少feature数来降低复杂度

Given n features, there are possible feature subsets, thus feature selection can be posed as a model selection problem over possible models.

显然计算和比较那么多的模型是不现实的，所以我们用heuristic search procedure，启发式的方式，去找到一个good feature subset，

forward search OR backward search

属于贪心算法，forward是一个个加，backward是一个个减，然后每次加减都通过cross validation做次局部最优的选择，即加个误差最小的，或减个误差最大的
这种需要通过训练测试的方式来选择的，称为wrapper model feature selection，因为它就像wrapper，需要反复调用学习算法来评估feature。
wrapper模型效果还是不错的，问题就是计算量比较大，需要调用这个数量级的次数的训练算法

Filter feature selection

效果没有wrapper那么好，但是比较cheaper，思路就是计算每个feature的score S(i) that measures how informative each feature xi is about the class labels y，最终我们只需要pick分数最高的那k个features就可以了，最常用的score就是mutual information
In practice, it is more common (particularly for discrete-valued features xi) to choose S(i) to be the mutual information MI(xi, y) between xi and y:

为了更直观的理解mutual information，这个式子还可以表示成，Kullback-Leibler (KL) divergence:

这个KL表示p(xi, y) and p(xi)p(y)的差异程度，
如果x和y是没有关系的，即独立的，那么 ，即KL-divergence为0

 

特征选择常用算法综述，这篇综述很好，看这个就ok了

 

Bayesian statistics and regularization

这节内容主要讨论如何用贝叶斯规范化来解决过拟合(overfit)问题

可以想想前面碰到的回归问题，都是用的最大似然估计，

即找到让训练集最为正确的那组参数，这样很容易过拟合
从统计学上看，最大似然估计，是一种frequentist statistics，即仅仅用频率来客观的估计概率，不加入任何主观的先验观念
对于这里，就是完全根据客观出现的训练集来估计真实的参数
并且对于frequentist 而言，最优参数是客观存在的，这里只是估计出他的真实值，所以式子中用的是“；”而不是“，”，表示本身并不作为条件

Frequentist or Bayesian

http://cos.name/2012/12/the-odyssey-of-stat-frequentist-or-bayesian/

那么在统计学中，对应于frequentist statistics的学派，叫Bayesian statistics
对于Bayesian而言，首先参数是个随机值，任何值都有可能，只是出现概率不同而已
再者，对于未知的参数，Bayesian会先给出主观的先验概率p()作为基础，再结合客观频率，综合给出结果

根据bayes定理，S表示训练集

分子比较好理解，分母我不理解，不过没事，反正仅仅需要比较大小，分母都是可以略去的

于是可以得到，

可以看看和上面极大似然的差别，
首先这里是作为条件的，注意是“，”而不是前面的“；”，但这其实并不影响p的计算，无论“，”或“；”，p的计算公式都是一样的
所以真正的不同只是加上了先验概率p()

为何加上先验概率就可以防止过拟合？

对于先验概率p()，常常是使用高斯分布（当然也可以使用其他的，但是高斯最常见）

你可以想想对于均值为0的高斯分布，如果要让p() max，那么就越接近于0
当为0时，相当于消除了一维，就达到了balance模型复杂度的效果

实际的效果证明， Bayesian logistic regression在文本分类上有很好的效果，即便对于文本分类，特征数n要远远大于训练集m

 

下面的内容其实在第11课占很多的时间，但是在讲义中是没有的
关注的问题，其实可以说是ML实战，觉得挺有意义的，所以记录在这里

Debugging Learning Algorithms

在使用ML算法，一定会碰到的问题是，如果算法实验的效果或准确率很差，我们应该怎样改进？

比如，用贝叶斯logistics回归做垃圾邮件过滤，结果误差有20%，如何改进？
原因有可能有很多，
训练样本集不够多，增加训练样本 （高variance）
特征太多，减少特征数                （高variance）
特征太少，增加特征数                 （高bias）
特征选取的不恰当，选取更好的特征  （高bias）

梯度下降迭代的不够多，没有收敛     （优化算法问题）
或应该使用其他的最优化算法，如牛顿 （优化算法问题）
目标函数中的参数不够合理，调节参数 （目标函数问题）
可能应该使用SVM。。。。。。        （目标函数问题）

当然可能有几百种改进的方法，其中一些是有效的，也许是无效的，但都会耗费很多的时间
所以，我们需要准确的找到优化的方向

首先需要确定的一点就是，当前的误差是高bias还是高variance？

这个其实很简单，
如果训练误差远远小于测试误差，那么一定是高variance误差
如果是高bias，那么训练误差也一定会很大，比如用线性函数去拟合二次函数

那么对于高variance误差，增加训练集就会比较有效果
因为随着训练集m的增大，测试误差会逐渐变小，而训练误差会逐渐变大，从而缩小他们之间的差距
为何训练集m变大，训练误差会变大，因为训练集越大，就越难完美的拟合

而对于高bias误差，训练误差已经超出预期，那么增加训练集是没有任何效果的，因为增加训练集只会更多增加训练误差，而也无法减小测试误差

 

其次，需判断的是，到底是因为优化算法有问题导致没有收敛，还是目标函数本身就选择的不对？
比如还是上面的例子，
你用贝叶斯logistics回归做垃圾邮件过滤，发现结果不是很满意，于是你使用SVM试了下，发现结果比较好，但是出于简单和效率考虑，你还是想用贝叶斯logistics回归
此时如何定位问题？
这里对于贝叶斯logistics回归或SVM，最终的目标都是拟合出最优的θ参数，即找到使目标函数J(θ)最大的θ
那么这里我们可以把logistics回归或SVM得到的参数θ1和θ2，都代入贝叶斯logistics回归的目标函数J(θ)中，

如果J(θ1) < J(θ2), 即SVM确实找到了更优的参数θ，那么一定是我们的优化函数有问题，没有收敛到最优参数
如果J(θ1) > J(θ2), 即SVM找到的参数不是更优参数，但是他实际的分类效果却比贝叶斯logistics回归好，说明当前的目标函数无法很好的描述这个问题，需要改变目标函数

其实我觉得这个方法有个问题，就是一定要找到类似SVM这样比当前算法效果好的相应算法
NG又举了个他做直升机自动驾驶的例子，如果发现效果不好，可能的原因有
直升机模拟器，无法模拟真实环境
使用的强化学习算法有问题，无法收敛
目标函数或Cost function有问题

那么他是如何来进行诊断的？
首先他要确认是否是模拟环境的问题，方法是用训练出的参数，分别在模拟环境和真实环境中实验，如果模拟环境中运行的很好，而真实环境的效果很差，那么就是模拟环境有问题
再者，和上面的思路一样，要找到一个比当前效果好的case
上面使用的是SVM，而这里他是让人来实际驾驶直升机从而得到一组参数，人驾驶的效果一定是很好的
下面就和上面一样，如果这组参数是更优参数，那么就是最优化算法的问题，否则就是目标函数有问题

 

Error Analysis

这个其实是一个比较简单的思路

因为在实际系统中，会有很多组件组成，当我们要优化这个系统时，首先需要知道这个系统的bottleneck在什么地方
比如，NG举例，从图片中识别人的系统，
会有，背景去除，人脸识别，眼睛识别，鼻子识别，logistics回归算法。。。
到底优化哪个会对系统的整体提升最大

方法是，如果要知道这个模块提升的空间，就将该模块替换成基准值，即100%正确的值，这样看系统准确率的提升

比如将背景去除替换成基准值时，准确率从80%提升到81%，那么你就知道这是不值得优化的，因为就是优化到100%也只能提升整体的1%
如果将人脸识别替换成基准值，准确率从80%提升到90%，那么你就知道这就是系统的bottleneck

另外一个思路也很自然，就是当系统有很多特性的时候，你想知道到底每个特性对系统的贡献有多大？
比如对于垃圾邮件分类，你加了一些特别的特性，发送IP，标点符号，语法分析
如果想知道，每个特性对系统的贡献，

方法是，把这个特性拿掉，看看系统的损失是多大，称为ablate分析