大数据索引技术 - B+ tree vs LSM tree
MySQL索引背后的数据结构及算法原理, http://www.codinglabs.org/html/theory-of-mysql-index.html
HBase Architecture, http://duanple.blog.163.com/blog/static/70971767201191661620641/
数据库如何抵抗随机IO:问题、方法与现实, http://wangyuanzju.blog.163.com/blog/static/13029201132154010987/?utm_source=twitterfeed&utm_medium=twitter
我们要讨论的是大数据的索引存储和数据结构问题...
首先要看看关系型数据库的B树索引, 关于这个问题MySQL索引背后的数据结构及算法原理讲的比较清楚, 这儿我简单的概述一下,
什么是索引?
在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用(指向)数据,这样就可以在这些数据结构上实现高级查找算法。这种数据结构,就是索引。
什么数据结构可以作为数据库索引?
对于数据库而言,使用树系列, 二叉树, 红黑树, B树, B+树, 因为要考虑到range查询, 所以hash索引不行
对于关系数据库, 基本都是用B+树作为索引机制, 而没有用二叉树或他的变种红黑树的, 为什么了?
一般来说,索引本身也很大,不可能全部存储在内存中,因此索引往往以索引文件的形式存储的磁盘上。这样的话,索引查找过程中就要产生磁盘I/O消耗,相对于内存存取,I/O存取的消耗要高几个数量级,所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的渐进复杂度。换句话说,索引的结构组织要尽量减少查找过程中磁盘I/O的存取次数。
那么为什么B+树, 能在尽量少的磁盘I/O的情况下进行检索了?
主存和磁盘以页为单位交换数据(在许多操作系统中,页得大小通常为4k), 页是计算机管理存储器的逻辑块, 原因就是磁盘一次读, 需要一系列机械操作, 而根据局部性原理: 当一个数据被用到时,其附近的数据也通常会马上被使用。
所以, 操作系统会进行预读, 这就意味着, 就算你只需要1byte的数据, 每次也要读一页出来. 所以如果想要减少磁盘读取次数, 就需要合理的组织存储结构, 使每次读出的页中包含更多我们需要的信息.
可以想象在遍历索引树的时候, 如果所有的树节点都是存在磁盘上的, 那么我们需要访问节点的个数, 就是我们实际需要的磁盘I/O次数. 因为你无法保证你读出一个page里面包含你想遍历的多个节点.
对于索引树而言, 访问次数等于树高, 那么即树高越高的树型结构, 效率越低.
所以对于平衡二叉树, 树高等于log2N, 明显效率太低.
于是产生了B树, B树就是增加每个节点的度, 度由2变成n, 这样树高大大降低, 一般实际只有3左右.
这个想法很自然, 我们使一个节点包含尽可能多的信息, 由2个分支到n个分支, 但是又要保证一个节点的信息必须在一个page中, 不能超出page大小.
数据库系统的设计者巧妙利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的,在实际实现B-Tree还需要使用如下技巧:
每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个node只需一次I/O。
这样就充分利用了每次page读, 不会出现之前的读4k, 而只有1byte有用的情况,
在page大小固定的情况下, B树的度是由每个度的大小(keysize + datasize + pointsize)决定的, 当然希望B树的度尽量的大, 这样树高就越低.
这个就是B+树产生的原因, 因为在B树中节点是存放data的, 而在B+树中所以data都放到了leaf节点, 这样就是树节点的度得到了大大的提高.
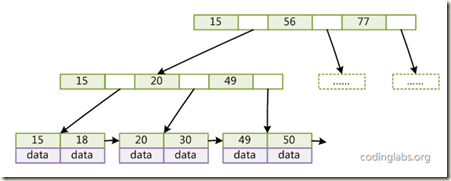
而数据库实际使用的是带有顺序访问指针的B+Tree, 如图
在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针,就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能
面对海量随机更新的索引问题?
接着, 既然B+树挺好, 为啥需要LSM-trees技术 (见后面的详细补充)
如果没有太多的随机更新操作,B+树可以工作地很好.Random IO for writes is bad
LSM Trees convert random writes to sequential writes
Writes go to a commit log and in-memory storage (Memtable)
The Memtable is occasionally flushed to disk (SSTable)
The disk stores are periodically compacted
但是当越快越多地将数据添加到随机的位置上, 会导致无法保证单个B+ tree节点能够存在一个disk page上, 页面就会变得碎片化.
这样读取一个tree node需要多次磁盘seek, 效率会极大的下降.
当然可以使用优化进程不断进行优化, 所以少量的随机更新是没有问题的
但对于海量随机更新, 比如HBase的case, 数据传入的速度可能会超过优化进程重写现存文件的速度, 导致效率底下.
HBase definite guide 中architecture章节中,
B树和LSM-tree本质上的不同点,实际上在于它们使用现代硬件的方式,尤其是磁盘。
对于大规模场景,计算瓶颈在磁盘传输上。CPU RAM和磁盘空间每18-24个月就会翻番,但是seek(磁盘寻道)开销每年大概才提高5%。
如前面所讨论的,有两种不同的数据库范式,一种是Seek,另一种是Transfer。RDBMS通常都是Seek型的,主要是由用于存储数据的B树或者是B+树结构引起的,在磁盘seek的速率级别上实现各种操作,通常每个访问需要log(N)个seek操作。另一方面,LSM-tree则属于Transfer型。在磁盘传输速率的级别上进行文件的排序和merges以及log(对应于更新操作)操作。
LSM-tree工作在磁盘传输速率的级别上,同时可以更好地扩展到更大的数据规模上。同时也能保证一个比较一致的插入速率,因为它会使用日志文件+一个内存存储结构把随机写操作转化为顺序写。读操作与写操作是独立的,这样这两种操作之间就不会产生竞争。
如何解决高速读写的balance问题?
http://blog.csdn.net/anderscloud/article/details/7181085
其实从本质来说,k-v存储要解决的问题就是这么一个:尽可能快得写入,以及尽可能快的读取
尽可能快得写
对磁盘来说,最快的写入方式一定是顺序的将每一次写入都直接写入到磁盘中即可。
但这样带来的问题是,我没办法查询,因为每次查询一个值都需要遍历整个数据才能找到. 典型的例子是HDFS, 支持海量写和顺序读, 不支持随机读
尽可能快的读
如果需要尽可能快的读到, 保持所有数据都是有序的, 就可以很快的读到. 典型的例子就是B+树.
但是需要保持全局有序, 必然会比较大的影响写的效率, 这就是B+树的问题. 如果有大量的随机写, 每个写都可能需要操作不同的磁盘文件, 效率很低, 而且影响磁盘利用率, 大量磁盘碎片.
所以不可能同时达到读和写的快速, 最终的方案就是折衷...牺牲部分读速度, 来保证写速度
这个就是LSM-tree和SSTable的原理,
保持部分有序, 并将部分有序的集合批量写入磁盘
B+树的读复杂度, 是log2n
而SSTable的读复杂度, (n/m)log2m. 把n分为大小为m的(n/m)个小集合, 每个集合都是有序的.
可以看出读的效率是低于B+ tree的, 但是由于写的效率大大提高, 因为总是顺序写.
当然这儿有其他方法提升读效率,
1. bloom filter
2. 小集合并成大集合, compact的过程
另一篇blog上有更多的介绍,
索引的随机IO问题要更复杂一点。我们简单点,只说涉及到单个索引项的操作。传统的B+树,无论是搜索、插入还是删除(更新相当于插入+删除,就不额外讨论了),理论上都是O(log(B)(N))次IO(其中B是页面包含的键值数,N是总键值数),但实际情况下可以假设非叶节点都在内存中,因此是1次 IO。磁盘一般只能有每秒几百次随机IO,因此对大的索引,每秒只能有几百次操作,这个性能真是低的可怜。B+树是70年代的老怪物,但直到今天,大多数数据库里仍然用得是它,但实际上,有比传统B+树更能对付随机IO的东西。
1996年,P O'Neil等提出的LSM-Tree是一个重大突破。
LSM-Tree主要有两种变形,最简单的LSM-Tree,是一个内存中的小索引加上外存中的大索引,更新先缓存在小索引中,再批量更新到大索引,这样就有望合并对属性同一页面的多次更新的IO。
复杂的LSM-Tree,是划分为多个level的很多的小索引,每个level的大小,近似的是前一个 level大小的r倍,如果一个level有r个小索引,则合并形成一个下一level的较大的索引,这样随机插入或删除的平均IO开销可以降低到 log(N)/B次,是一个很大的提升。
但带来的问题是,搜索的时候,就要搜索这么多个小索引,而这样的索引会有O(log(N/B))个,那是可能有几十个,搜索的性能就可能下降几十倍,这往往也带来问题。LSM-Tree已经有不少的现实应用,BigTable、Cassandra、Lucene等这些用的是复杂的那种LSM-Tree,InnoDB的change buffer可以说是那种一大一小的简单LSM-Tree。NTSE想在做多版本事务的时候顺便实现change buffer。
2000年,MA Bender等提出的Cache Oblivious B-Tree是第二个重大突破。这个跟LSM-Tree有些类似,也是索引从小到大分成相邻大小翻倍的多个索引,因此随机插入或删除的平均IO开销也是log(N)/B次,但它用了Fractional Cascading的技术,使得搜索的性能较传统B+树相关不多。虽然论文发表了10年了,这种索引似乎现在只有TokuDB一家实现,它是称之为Fractal Tree。我们拿来试了试,效果果然出奇的好。
有没有可能将来搞出一个比Fractal Tree更好的东西呢,遗憾的是如果硬件不发生根本改变,已经证明Fractal Tree已经是最理想的了。