【CodeForces 297C】Splitting the Uniqueness
题意
序列s有n个数,每个数都是不同的,把它每个数分成两个数,组成两个序列a和b,使ab序列各自去掉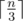 个数后各自的其它数字都不同。
个数后各自的其它数字都不同。
如果存在一个划分,就输出YES,并且输出两个序列,否则输出NO。
分析
两个月前做的一题,那时候问学长才会做的,现在刚看到题又懵逼了。再做过了一遍。
序列s的每个数都是不同的,我们先给s按递增排序,然后构造:k=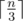
前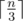 个数 个数 |
第二个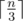 个数 个数 |
剩下≤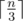 个数 个数 |
|
| s | s[i] | s[i+k] | s[i+2*k] |
| a | s[i] | 0 | |
| b | 0 | s[i+k] | 0 1 2 ... ..2 1 0 即k-i |
1≤i≤k
分配完前两段,问题变成除去k个0后,剩下的数都要不同。
因为i每增加1,s[i]至少增加1,所以 b的第k+1个数≥k,也就是是说b这个序列中间那一段数是≥k的,那后面≤k个数就可以放上0到k-1了。因为s[i]递增了,要让si-bi的数也不同,那bi要递减才能保证。那会不会和前面冲突呢?不会。因为a的第三段最小的是i=1时的s[i+2*k]-k+1,a第一段最大的是s[k],又因为si是互不相同的,所以有s[i+2*k]-s[k]≥k+1,所以s[i+2*k]-k+1-s[k]≥2,所以a第三段所有数都大于第一段任意数。
cf上题解的做法是
前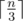 个数 个数 |
第二个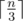 个数 个数 |
剩下≤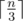 个数 个数 |
|
| s | s[i] | s[i+k] | s[i+2*k] |
| a | 0 1 2... k-1 | ||
| b | k k+1 k+2 ... | ..2 1 0 即k-i |
代码
#include<cstdio> #include<algorithm> using namespace std; const int N=1e5+10; struct p { int v,id,s; } a[N]; bool cmp(p a,p b) { return a.v<b.v; } bool cmp1(p a,p b) { return a.id<b.id; } int n; int main() { scanf("%d",&n); for(int i=1; i<=n; i++) { scanf("%d",&a[i].v); a[i].id=i; } printf("YES\n"); sort(a+1,a+1+n,cmp); int k=n/3; if(n%3) k++; for(int i=1; i<=k; i++) { a[i].s=0; a[i+k].s=a[i+k].v; a[i+k*2].s=k-i; } sort(a+1,a+1+n,cmp1); for(int i=1; i<n; i++) { printf("%d ",a[i].s); } printf("%d\n",a[n].s); for(int i=1; i<n; i++) { printf("%d ",a[i].v-a[i].s); } printf("%d\n",a[n].v-a[n].s); return 0; }
┆凉┆暖┆降┆等┆幸┆我┆我┆里┆将┆ ┆可┆有┆谦┆戮┆那┆ ┆大┆始┆ ┆然┆
┆薄┆一┆临┆你┆的┆还┆没┆ ┆来┆ ┆是┆来┆逊┆没┆些┆ ┆雁┆终┆ ┆而┆
┆ ┆暖┆ ┆如┆地┆站┆有┆ ┆也┆ ┆我┆ ┆的┆有┆精┆ ┆也┆没┆ ┆你┆
┆ ┆这┆ ┆试┆方┆在┆逃┆ ┆会┆ ┆在┆ ┆清┆来┆准┆ ┆没┆有┆ ┆没┆
┆ ┆生┆ ┆探┆ ┆最┆避┆ ┆在┆ ┆这┆ ┆晨┆ ┆的┆ ┆有┆来┆ ┆有┆
┆ ┆之┆ ┆般┆ ┆不┆ ┆ ┆这┆ ┆里┆ ┆没┆ ┆杀┆ ┆来┆ ┆ ┆来┆


