四则运算

GitHub地址：https://github.com/fenglimao/text

在开始实现程序之前，在下述PSP表格记录下你估计将在程序的各个模块的开发上耗费的时间

PSP表格：

		预计耗时（分钟）
Planning	计划	60
Estimate	估计这个任务需要多少时间	600
Development	开发	240
Analysis	需求分析	15
Design Spec	生成设计文档	/
Design Review	设计复审（和同事审核设计文档）	/
Coding Standerd	代码规范（为目前的开发制定合适的规范）	/
Design	具体设计	20
Coding	具体编码	60
Code Review	代码复审	10
Text	测试（自测，修改代码，提交修改）	10
Reporting	报告	30
Text Report	测试报告	30
Size Measurement	计算工作量	10
Postmortem & Process Improvement Plan	事后总结，并提出过程改进计划	15
Sum	合计	500

解题思路描述。即刚开始拿到题目后，如何思考，如何找资料的心路历程。

拿到题目赶紧百度寻找代码，但是只能找到相类似的代码，所以就把它修改为python的代码、要实现的是四则运算的代码还是很多的，但要求不能出现负数就比较麻烦，所以百度一下并且问了同学该如何操作。最后，通过自己不懈的努力还有同学的帮助最后还是做了个比较简单的作业。

设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？

题目：

　　（1）能自动生成小学四则运算题目，并且不能出现负数；

　　（2）能支持真分数的四则运算；

实现过程：

　　设计三个函数：

　　　　def newint() 生成整数四则运算

　　　　def newfra() 生成真分数四则运算

　　　　def newtest() 生成制定指定数量的四则运算题目

　　函数关系：

　　　　newint()与newfra()为独立的函数，负责生成随机四则运算，newtest()则随机调用上述两个函数生成题目。详细描述请看下方代码说明

代码说明。展示出项目关键代码，并解释思路与注释说明

首先说明整数的四则运算，生成两个随机数并随机运算，在减法中比较大小防止出现负数，在除法中比较大小并循环取整除的随机数组合。最后输出算式并返回正确答案。

def newint():

    opr = ['＋', '－', '×', '÷']

    fh = random.randint(0, 3)

    n1 = random.randint(1, 20)

    n2 = random.randint(1, 20)

    rjg = 0

    if fh == 0:

        rjg = n1 + n2

    elif fh == 1:

        n1, n2 = max(n1, n2), min(n1, n2)

        rjg = n1 - n2

    elif fh == 2:

        rjg = n1 * n2

    elif fh == 3:

        n1, n2 = max(n1, n2), min(n1, n2)

        while n1 % n2 != 0:

            n1 = random.randint(1, 10)

            n2 = random.randint(1, 10)

            n1, n2 = max(n1, n2), min(n1, n2)

        rjg = int(n1 / n2)

    print(n1, opr[fh], n2, '= ', end='')

    return rjg

　　真分数四则运算类似。

def newfra():

    opr = ['＋', '－', '×', '÷']

    fh = random.randint(0, 3)

    t1 = random.randint(1, 10)

    t2 = random.randint(t1, 10)

    n1 = Fraction(t1, t2)

    t1 = random.randint(1, 10)

    t2 = random.randint(t1, 10)

    n2 = Fraction(t1, t2)

    rjg = 0

    if fh == 0:

        rjg = n1 + n2

    elif fh == 1:

        n1, n2 = max(n1, n2), min(n1, n2)

        rjg = n1 - n2

    elif fh == 2:

        rjg = n1 * n2

    elif fh == 3:

        n1, n2 = max(n1, n2), min(n1, n2)

        rjg = n1 / n2

    print(n1, opr[fh], n2, '= ', end='')

    return rjg

　def newtest():

    opr = ['＋', '－', '×', '÷']

    print('输入题库所需要的题目数量')

    n=int(input())

    rjg=[]

    m=0

    while m<=(n-1):

        fh = random.randint(0, 4)

        if fh==0:

            print(m+1,end='、')

            rjg.append(newfra())

            print(' ')

        else:

            print(m+1,end='、')

            rjg.append(newint())

            print(' ')

        m=m+1

    m=0

    print('答案：')

    while m<=(n-1):

        print(m+1,'、',rjg[m])

        m=m+1

print('1、四则运算')

print('2、制作题库')

n=int(input())

if n==1:

    print('input "0000" to Quit')

    while True:

        fh = random.randint(0, 4)

        if fh == 0:

            rjg = newfra()

            jg = input()

            if jg == '0000':

                break;

            sr = Fraction(jg)

            if sr == rjg:

                print('right')

            else:

                print('error. the Tight answer is', rjg)

        else:

            rjg = newint()

            jg = input()

            if jg == '0000':

                break;

            sr = int(jg)

            if sr == rjg:

                print('right')

            else:

                print('error. the Tight answer is', rjg)

if n==2:

    newtest()

测试运行。程序必须是可运行的，展示出程序运行的截图。

记录在改进程序性能上所花费的时间，描述你改进的思路，并展示一张性能分析图，并展示你程序中消耗最大的函数。

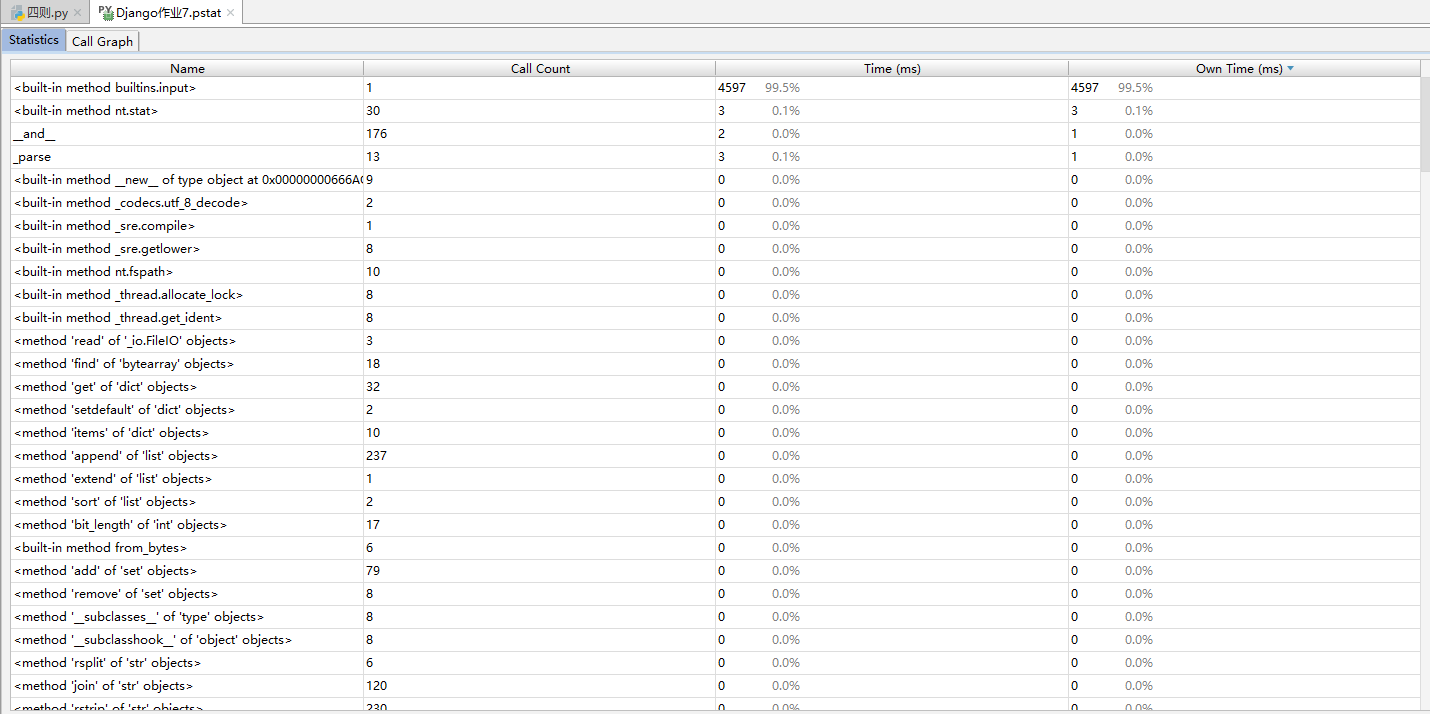
在你实现完程序之后，在下述PSP表格记录下你在程序的各个模块上实际花费的时间