粒子滤波概述

粒子滤波(PF: Particle Filter)的思想基于蒙特卡洛方法(Monte Carlo methods)，它是利用粒子集来表示概率，可以用在任何形式的状态空间模型上。其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布，是一种顺序重要性采样法(Sequential Importance Sampling)。简单来说，粒子滤波法是指通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差分布的过程。这里的样本即指粒子,当样本数量N→∝时可以逼近任何形式的概率密度分布。

尽管算法中的概率分布只是真实分布的一种近似，但由于非参数化的特点，它摆脱了解决非线性滤波问题时随机量必须满足高斯分布的制约，能表达比高斯模型更广泛的分布，也对变量参数的非线性特性有更强的建模能力。因此，粒子滤波能够比较精确地表达基于观测量和控制量的后验概率分布，可以用于解决SLAM问题。

粒子滤波的应用

粒子滤波技术在非线性、非高斯系统表现出来的优越性，决定了它的应用范围非常广泛。另外，粒子滤波器的多模态处理能力，也是它应用广泛有原因之一。国际上，粒子滤波已被应用于各个领域。在经济学领域，它被应用在经济数据预测；在军事领域已经被应用于雷达跟踪空中飞行物，空对空、空对地的被动式跟踪；在交通管制领域它被应用在对车或人视频监控；它还用于机器人的全局定位。

粒子滤波的缺点

虽然粒子滤波算法可以作为解决SLAM问题的有效手段，但是该算法仍然存在着一些问题。其中最主要的问题是需要用大量的样本数量才能很好地近似系统的后验概率密度。机器人面临的环境越复杂，描述后验概率分布所需要的样本数量就越多，算法的复杂度就越高。因此，能够有效地减少样本数量的自适应采样策略是该算法的重点。另外，重采样阶段会造成样本有效性和多样性的损失，导致样本贫化现象。如何保持粒子的有效性和多样性，克服样本贫化，也是该算法研究重点。

粒子滤波的发展

1.MCMC改进策略

马尔可夫链蒙特卡洛(MCMC)方法通过构造Markov链，产生来自目标分布的样本，并且具有很好的收敛性。在SIS的每次迭代中，结合MCMC使粒子能够移动到不同地方，从而可以避免退化现象，而且Markov链能将粒子推向更接近状态概率密度函数(probabilitydensityfunction,(PDF))的地方，使样本分布更合理。基于MCMC改进策略的方法有许多，常用的有Gibbs采样器和MetropolisHasting方法。

2.Unscented粒子滤波器(UPF)

UnscentedKalman滤波器(UKF)是Julier等人提出的。EKF(ExtendedKalmanFilter)使用一阶Taylor展开式逼近非线性项，用高斯分布近似状态分布。UKF类似于EKF，用高斯分布逼近状态分布，但不需要线性化只使用少数几个称为Sigma点的样本。这些点通过非线性模型后，所得均值和方差能够精确到非线性项Taylor展开式的二阶项，从而对非线性滤波精度更高。Merwe等人提出使用UKF产生PF的重要性分布，称为Unscented粒子滤波器(UPF)，由UKF产生的重要性分布与真实状态PDF的支集重叠部分更大，估计精度更高。

3.Rao－Blackwellised粒子滤波器(RBPF)

在高维状态空间中采样时,PF的效率很低。对某些状态空间模型，状态向量的一部分在其余部分的条件下的后验分布可以用解析方法求得，例如某些状态是条件线性高斯模型，可用Kalman滤波器得到条件后验分布，对另外部分状态用PF，从而得到一种混合滤波器，降低了PF采样空间的维数，RBPF样本的重要性权的方差远远低于SIR方法的权的方差，为使用粒子滤波器解决SLAM问题提供了理论基础。而Montemerlo等人在2002年首次将Rao-Blackwellised粒子滤波器应用到机器人SLAM中，并取名为FastSLAM算法。该算法将SLAM问题分解成机器人定位问题和基于位姿估计的环境特征位置估计问题，用粒子滤波算法做整个路径的位姿估计，用EKF估计环境特征的位置，每一个EKF对应一个环境特征。该方法融合EKF和概率方法的优点，既降低了计算的复杂度，又具有较好的鲁棒性。

最近几年，粒子方法又出现了一些新的发展，一些领域用传统的分析方法解决不了的问题，现在可以借助基于粒子仿真的方法来解决。在动态系统的模型选择、故障检测、诊断方面，出现了基于粒子的假设检验、粒子多模型、粒子似然度比检测等方法。在参数估计方面，通常把静止的参数作为扩展的状态向量的一部分，但是由于参数是静态的，粒子会很快退化成一个样本，为避免退化，常用的方法有给静态参数人为增加动态噪声以及Kernel平滑方法，而Doucet等提出的点估计方法避免对参数直接采样，在粒子框架下使用最大似然估计(ML)以及期望值最大(EM)算法直接估计未知参数。

clc

clear all

close all

 

% Particle filter example, adapted from Gordon, Salmond, and Smith paper.

 

x = 0.1; % initial state

Q = 1; % process noise covariance

R = 1; % measurement noise covariance

tf = 50; % simulation length

 

N = 200; % number of particles in the particle filter

 

xhat = x;

P = 2;

xhatPart = x;

 

% Initialize the particle filter.

for i = 1 : N

    xpart(i) = x + sqrt(P) * randn;

end

 

xArr = [x];

yArr = [x^2 / 20 + sqrt(R) * randn];

xhatArr = [x];

PArr = [P];

xhatPartArr = [xhatPart];

 

for k = 1 : tf

    % System simulation

    x = 0.5 * x + 25 * x / (1 + x^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;%×′ì?·?3ì

    y = x^2 / 20 + sqrt(R) * randn;%1?2a·?3ì

    % Particle filter

    for i = 1 : N

        xpartminus(i) = 0.5 * xpart(i) + 25 * xpart(i) / (1 + xpart(i)^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;

        ypart = xpartminus(i)^2 / 20;

        vhat = y - ypart;%1?2aoí?¤2aμ?2?

        q(i) = (1 / sqrt(R) / sqrt(2*pi)) * exp(-vhat^2 / 2 / R);

    end

    % Normalize the likelihood of each a priori estimate.

    qsum = sum(q);

    for i = 1 : N

        q(i) = q(i) / qsum;%1éò??ˉè¨??

    end

    % Resample.

    for i = 1 : N

        u = rand; % uniform random number between 0 and 1

        qtempsum = 0;

        for j = 1 : N

            qtempsum = qtempsum + q(j);

            if qtempsum >= u

                xpart(i) = xpartminus(j);

                break;

            end

        end

    end

    % The particle filter estimate is the mean of the particles.

    xhatPart = mean(xpart);

 

    % Save data in arrays for later plotting

    xArr = [xArr x];

    yArr = [yArr y];

    xhatPartArr = [xhatPartArr xhatPart];

end

 

t = 0 : tf;

figure;

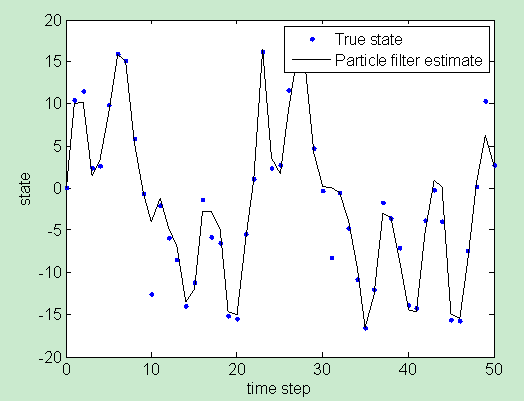
plot(t, xArr, 'b.', t, xhatPartArr, 'k-');

set(gca,'FontSize',12); set(gcf,'Color','White');

xlabel('time step'); ylabel('state');

legend('True state', 'Particle filter estimate');

 

xhatPartRMS = sqrt((norm(xArr - xhatPartArr))^2 / tf);

disp(['Particle filter RMS error = ', num2str(xhatPartRMS)]);