Softmax回归

1. softmax回归模型

　　softmax回归模型是logistic回归模型在多分类问题上的扩展（logistic回归解决的是二分类问题）。

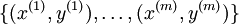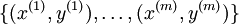　　对于训练集 $\{ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) \}$ ，有 $\{ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) \}$ 。

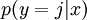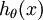　　对于给定的测试输入 $\textstyle x$ ，我们相拥假设函数针对每一个类别j估算出概率值 $\textstyle p(y=j | x)$ 。也就是说，我们估计 $\textstyle x$ 得每一种分类结果出现的概率。因此我们的假设函数将要输入一个 $\textstyle k$ 维的向量来表示这 $\textstyle k$ 个估计得概率值。假设函数 $\textstyle h_{\theta}(x)$ 形式如下：

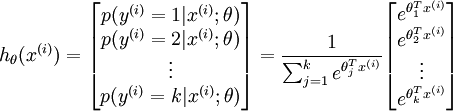
$\begin{align} h_\theta(x^{(i)}) = \begin{bmatrix} p(y^{(i)} = 1 | x^{(i)}; \theta) \\ p(y^{(i)} = 2 | x^{(i)}; \theta) \\ \vdots \\ p(y^{(i)} = k | x^{(i)}; \theta) \end{bmatrix} = \frac{1}{ \sum_{j=1}^{k}{e^{ \theta_j^T x^{(i)} }} } \begin{bmatrix} e^{ \theta_1^T x^{(i)} } \\ e^{ \theta_2^T x^{(i)} } \\ \vdots \\ e^{ \theta_k^T x^{(i)} } \\ \end{bmatrix} \end{align}$

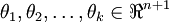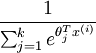　　其中 $\theta_1, \theta_2, \ldots, \theta_k \in \Re^{n+1}$ 是模型的参数。 $\frac{1}{ \sum_{j=1}^{k}{e^{ \theta_j^T x^{(i)} }} }$ 这一项对概率分布进行归一化，舍得所有概率之和为1.

　　softmax回归的代价函数：

$\begin{align} J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right] \end{align}$

　　上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为：

$\begin{align} J(\theta) &= -\frac{1}{m} \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\ &= - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=0}^{1} 1\left\{y^{(i)} = j\right\} \log p(y^{(i)} = j | x^{(i)} ; \theta) \right] \end{align}$

　　可以看到，softmax代价函数与logistic代价函数在形式上非常类似，只是在softmax损失函数中对类标记的 $\textstyle k$ 个可能值进行了累加。注意在softmax回归中将 $\textstyle x$ 分类为 $\textstyle j$ 的概率为：

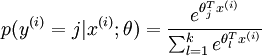
$p(y^{(i)} = j | x^{(i)} ; \theta) = \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)}} }$

$\begin{align} \nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} \left( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) \right) \right] } \end{align}$ 有了上面的偏导数公式以后，我们就可以将它代入到梯度下降法等算法中，来最小化 $\textstyle J(\theta)$ 。例如，在梯度下降法的标准实现中，每一次迭代需要进行如下更新: $\textstyle \theta_j := \theta_j - \alpha \nabla_{\theta_j} J(\theta)$

2. 权重衰减

在实际应用中，为了使算法实现更简单清楚，往往保留所有参数 $\textstyle (\theta_1, \theta_2,\ldots, \theta_n)$ ，而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动：加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。

$\begin{align} J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }} \right] + \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^n \theta_{ij}^2 \end{align}$

我们通过添加一个权重衰减项 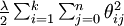$\textstyle \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^{n} \theta_{ij}^2$ 来修改代价函数，这个衰减项会惩罚过大的参数值，现在我们的代价函数变为：

有了这个权重衰减项以后 (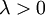 $\textstyle \lambda > 0$ )，代价函数就变成了严格的凸函数，这样就可以保证得到唯一的解了。此时的 Hessian矩阵变为可逆矩阵，并且因为 $\textstyle J(\theta)$ 是凸函数，梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。

为了使用优化算法，我们需要求得这个新函数 $\textstyle J(\theta)$ 的导数，如下：

$\begin{align} \nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j \end{align}$

通过最小化 $\textstyle J(\theta)$ ，我们就能实现一个可用的 softmax 回归模型。

3. 模型选择

如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？

这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 $k = 4 的softmax回归。$

如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品，我们的算法可以分别判断它是否属于各个类别。

现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？

在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

转自：http://www.cnblogs.com/Rosanna/p/3865212.html

参考：http://deeplearning.stanford.edu/wiki/index.php/Softmax回归

posted on 2016-04-19 16:42 大雄fcl 阅读(7301) 评论(0) 编辑收藏举报

刷新页面返回顶部

Softmax回归

公告