Quicksort in JavaScript

“快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。”

-- 维基百科

 

快速排序主要分为三个步骤

1. 从数列中挑选任意一个元素为基准(pivot)元素
2. 重新排序数列，把小于基准值的元素摆在基准的左边，将大于基准值的元素摆在基准的右边。这个操作称为分区(partition)操作，分区操作结束后，基准元素所处的位置就是最终排序后它的位置。
3. 递归地将小于基准和大于基准的两部分序列再进行分区操作，最终递归完成，排序结束。

 

分区步骤

分区是快速排序的主要内容，举例来说，我们现在有一个序列seq = [36  52  57  9  18  20  8  37  22]，分区可以分解成以下步骤：

 

① 首先选定一个基准元素，这里我们取第一个元素(36)为基准元素(可以为任意元素):

 

 

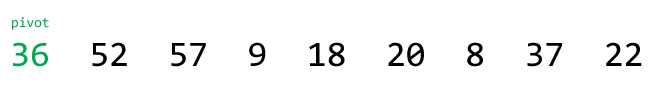
② 从左往右，以变量i代表索引(不包括基准元素,即初始i == 1)，找到第一个大于基准的数(i == 1, seq[i] == 52):

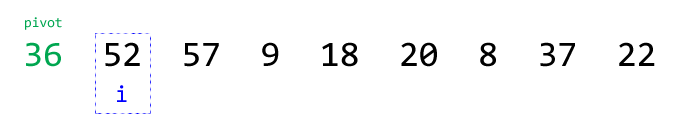
③ 从右往左，以变量k代表索引(初始k == seq.length - 1)，找到第1个小于等于基准的数(k == 8, seq[k] == 22):

 

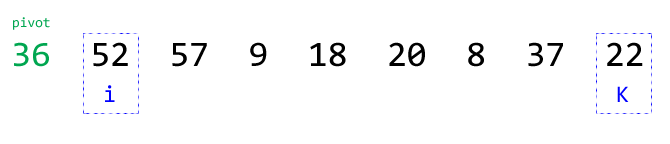
④ 交换元素seq[i]和seq[k]的位置(留意这里i < k,说明还有元素未遍历):

 

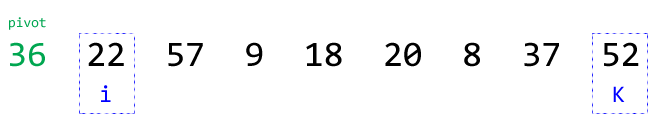
⑤ 重复步骤②，递增i，找到下一个大于基准的数(i == 2, seq[i] == 57):

 

 

⑥重复步骤③，递减k，找到下一个小于等于基准的数(k == 6, seq[k] == 8):

 

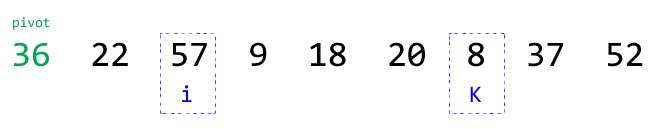
⑦重复步骤④，交换元素seq[i]和seq[k]的位置(留意这里i < k,说明还有元素未遍历):

 

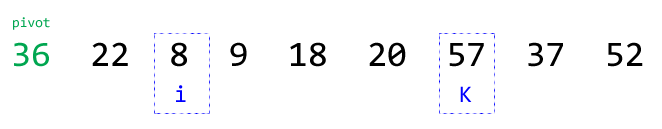
⑧重复步骤②，递增i，找到下一个大于基准的数(i == 7, seq[i] == 37):

 

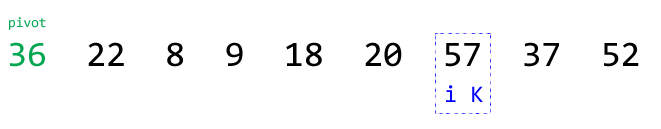
⑨重复步骤③，递减k，找到下一个小于等于基准的数(k == 5, seq[k] == 20):

 

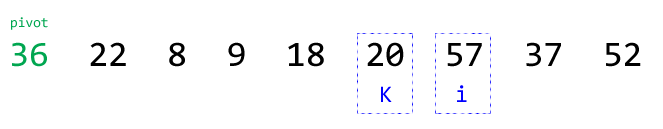
⑩ 此时i > k，我们不再调换元素seq[i]和seq[k]的位置，因为序列已经基本分区完成(除了基准元素)。我们可以观察到调换seq[pivot]和seq[k]的位置，序列即被完全分区成两部分：小于基准的部分和大于等于基准的部分：

 至此一轮分区操作完成。

 

 

快速排序只要递归地将分区后的两部分序列(不包括基准值)再进行分区，直到递归完成。即递归分区 seq[0] 至 seq[k - 1]， 和 seq[k + 1]至seq[length - 1]两部分:

 

Quicksort in Javascript

function quickSort(seq){
    return sort(seq, 0, seq.length - 1);

    function swap(seq, i, k){
        var tempVal = seq[i];
        seq[i] = seq[k];
        seq[k] = tempVal;
    }

    function sort(seq, start, end){
        if(start >= end) return;

        var pivot = seq[start],
            i = start + 1,
            k = end;

        while(true){
            while(i <= end && seq[i] < pivot) i++;
            while(k > start && seq[k] >= pivot) k--;

            if(i >= k) break;
            swap(seq, i, k);
        }

        swap(seq, start, k);
        sort(seq, start, Math.max(0, k - 1));
        sort(seq, Math.min(end, k + 1), end);
    }
}