个人项目作业
个人项目-数独
个人项目地址
https://github.com/ErisPluto/Sudoku解题思路
- 需求分析
- 生成终局:
- 命令格式: sudoku.exe -c N
- 1 <= N <= 1000000
- 输出到文件: sudoku.txt
- 数独不重复
- 数独左上角第一个数为(学号后两位相加)% 9 + 1 = (8 + 0) % 9 + 1 = 9
- 处理异常情况
- 求解数独:
- 命令格式: sudoku.exe -s absolute_path_of_puzzlefile
- 数独题目个数: 1 <= N <= 1000000
- 0代表空格,保证格式正确,对每个题目求出一个可行解
- 输出到文件: sudoku.txt
- 处理异常情况
- GUI设计(可选): 如果能够较好的完成前两部分再来考虑GUI
- 生成终局:
- 相关思路
- 首先需要花一些时间来学习C++,熟悉github和visual studio
- 对于生成数独终局,最先考虑到的是暴力回溯,逐个格从1-9遍历尝试。由于生成数独终局时左上角第一个格被限制,在回溯法的思路下,生成终局和求解数独其实是一样的。虽然肯定会慢,但是是一种明确的而且比较容易写的方法,因为自身编码能力不强,所以考虑到的就是先把功能实现再考虑性能的问题,所以决定使用回溯法,并没有考虑去网上找一些更好的算法。
- 关于文件的读写,最开始完全没有意识到文件读写花费的大量的时间,于是采用的是逐个读逐个写的方法。
设计实现
- 生成数独/求解数独
由于没有去网上找其他算法,所以基本上是离不开回溯法的,尽管如此,由于侧重点的不同还是前后改了三个版本
第一个版本非常希望能在不重复的基础上增加随机性,根本没有考虑性能的问题
在回溯法的思路下,希望能够给生成的数独终局一些随机性,而不是完全的按照规律,虽然没有尝试但是感觉完全的先随机后验证在产生大量数独时会有大量的冲突,因此考虑过预先存储、随机读取的方式。但是事实很快就告诉我,没有调查的实践最终很可能打脸。现在想想当时的行为略显天真:试图用回溯法把所有的数独终局生成出来,存在一个文件里,需要时随机生成一个index去文件中读取相应的行。后来过了很久发现仍然只是后面几行在发生变化,再这样下去可能C盘盛不下。去网上查了一下发现全部数独的数量是一个极其惊人的数字,甚至连多少位都没有数清,生成的文件能不能放得下先不说,可能文件读写花费的时间就让人很难承受了。
1.0夭折了,但是当时并没有意识到文件读写的成本,所以仍然不死心的做了1.5,把1-9的全排列生成后存到文件里,随机取出来填到第一行里并作为回溯的依据。第一次提交的就是这一版,理论上似乎比最开始的想法现实了一点,但是非常非常慢,亲测不可用。
-
在前一个版本失败后,基本上放弃了完全随机的想法,而是小范围的随机。即随机生成一个以9开头的1-9的排列作为初始数组,以此作为回溯的依据,一直回溯下去。经过数学计算,左上角第一格固定的话能够生成的不重复的数独是远远超过1000,000这个数字的,因此就采用了这样的方法。
回溯的具体过程用到row,column, square三个9 * 9的数组做标记,记为1,记录每一行、列、九宫格中已使用的数字在初始数组中的index。一个循环结束后回退时把标记抹去。
在求解数独时也是用了相同的方法,但是由于存在原始值,与原始值存在相关的标记不能抹去,为了区别,记为2。但是这里犯了一个严重的错误,直到第三版和测试才发现,遇到原始值应该直接跳过,但是这里把原始值的判断这一步写进了循环里,导致回退之后原始值被修改。
- 第三个版本中回溯法失去了主导地位,是在D同学的建议下做出的改进,在此非常感谢D同学,这一部分会在性能改进中详细说。
- 文件输入输出
- 最开始使用了逐个字符输入输出的方法,感觉1000,000个数组可能一小时都完不成。
- 后来改成了每个数独终局输出一次的方法,发现几乎没有什么改进。
性能改进
以下是优化后的CPU使用率s。
生成1000,000个数独终局需要4分10s,虽然还是很慢,但是比最开始已经好了很多。
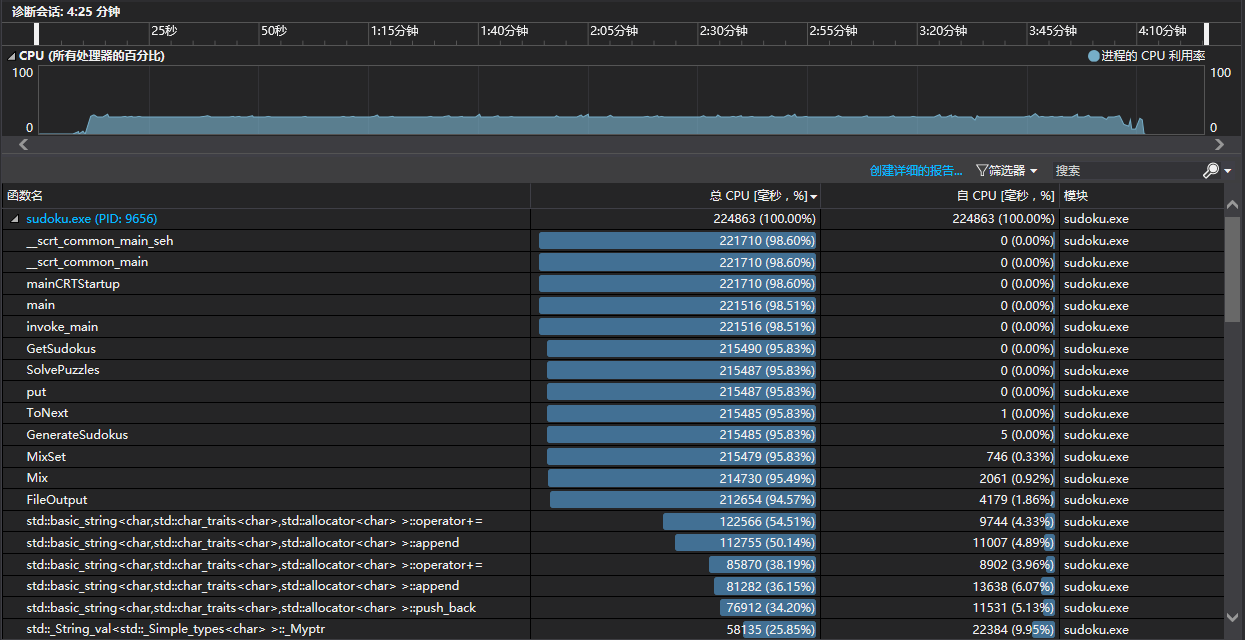
求解1000个数独花费的时间约为38s,文件输入输出更改后速度也提高很多。

单元测试,分别针对参数以及求解过程中的返回值所表示的运行情况测试
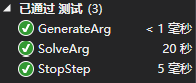
运行过程中函数的消耗
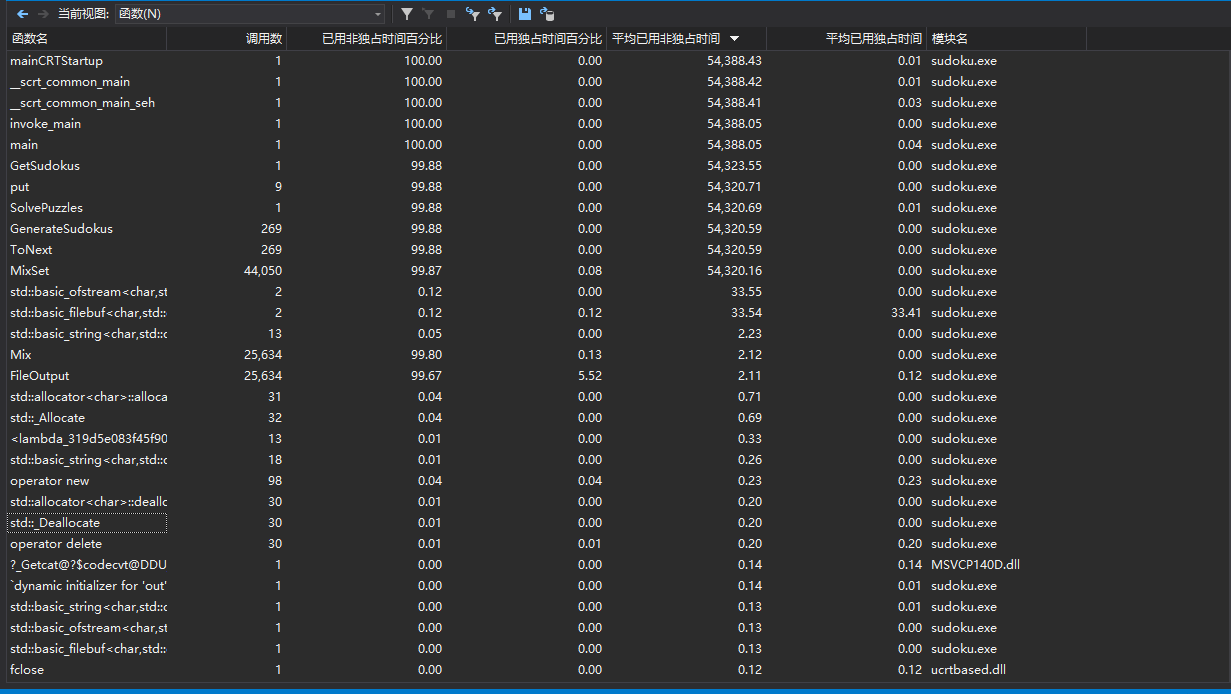
文件输入输出更改之后可以在10s内完成。
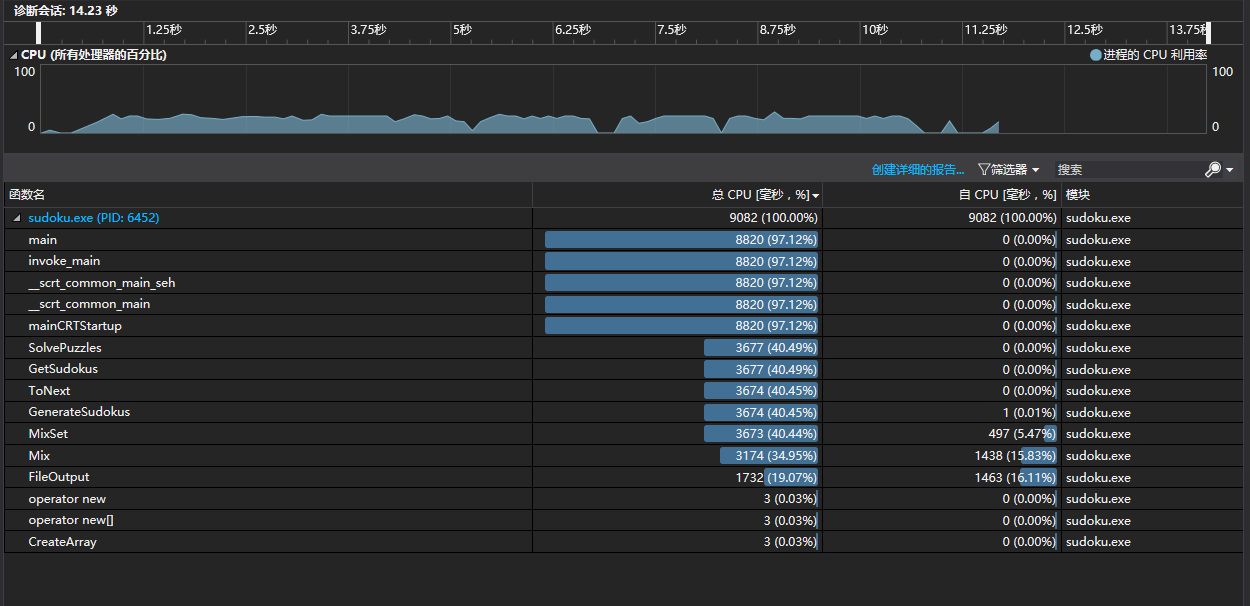
<ul>
<li>数独生成方法的改进
<ol>
<li>左上角第一格为9,所以先把9个9放到合法的位置中(回溯)</li>
<li>随机产生初始数组,用求解数独的方法(回溯)得到一个数独</li>
<li>遍历1-8的全排列,由初始数独进行映射,一个初始数独可以得到8!个数独</li>
<li>若已达到N则停止,否则返回第一步</li>
</ol>
<p>由每个初始数独产生的8!个数独是不重复的,另外9个9个位置不同也能够保证每个初始数独产生的数独都不重复。以下是流程图:</p>
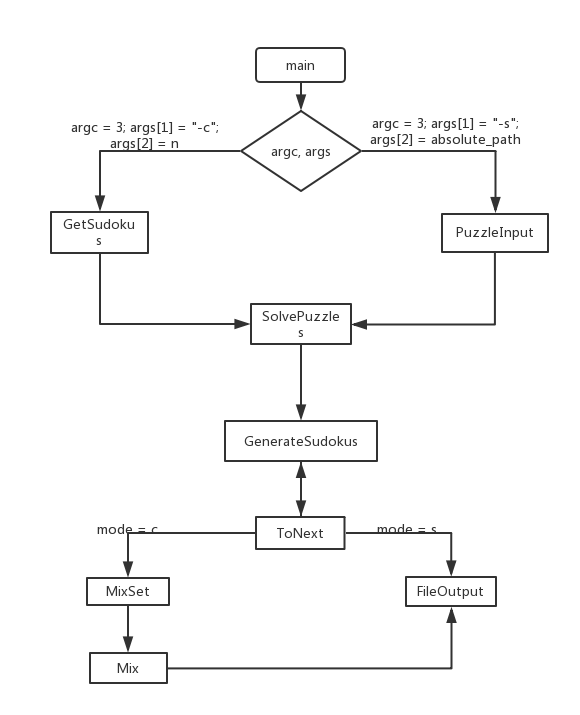
</li>
<li>文件输入输出方法的改进
<p>在使用了每个终局输出一次的方法之后发现输出1000,000个终局仍然需要一小时以上的时间,于是打算将N个终局存在string中一次性输出,将原来的输出函数改成了将二维数组改为字符串的函数,在main函数的结尾一次性输出</p>
<p>同理,也不再使用逐个字符读入的方法,而是用了ifstream,stringstream和string一次将文件中的内容读到string中,再转化为二维数组。后来发现string的拼接占用了大量的时间,于是直接使用字符数组,性能有了很大的提高。</p>
</li>
</ul>
代码说明
- 生成左上角第一格数字的分布
int GetSudokus(int i, int **sudoku, int *row, int *col, int *squa) {
int t = 0, j = 0, sign = 0;
for (j = 0; j < 9; j++) {
t = i / 3 * 3 + j / 3;
if (row[i] != 0 || col[j] != 0 || squa[t] != 0) {
continue;
}
sudoku[i][j] = FIX;
row[i] = col[j] = squa[t] = 1;
if (i == 8) {
sign = SolvePuzzles(CopyArray(sudoku), "sudoku.txt");
}
else {
sign = GetSudokus(i + 1, sudoku, row, col, squa);
}
if (sign == -1) {
return sign;
}
sudoku[i][j] = row[i] = col[j] = squa[t] = 0;
}
return sign;
} - 将分布作为要求解的数独,进行标记
int SolvePuzzles(int **puzzle, char *path) {
int **row = CreateArray(), **column = CreateArray(), **square = CreateArra ();
int i = 0, j = 0, t = 0;
int *initSet = InitSet();
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
t = i / 3 * 3 + j / 3;
if (puzzle[i][j] != 0) {
row[i][puzzle[i][j] - 1] = 2;
column[j][puzzle[i][j] - 1] = 2;
square[t][puzzle[i][j] - 1] = 2;
}
}
}
int sign = GenerateSudokus(initSet, row, column, square, puzzle, 0, 0, path);
DeleteArray(row);
DeleteArray(column);
DeleteArray(square);
return sign;
} - 求解初始数独
int GenerateSudokus(int *initSet, int **row, int **column, int **square, int **sudoku, int i, int j, char *path) {
int sign = 0;
if (sudoku[i][j] != 0) {
sign = ToNext(initSet, row, column, square, sudoku, i, j, path);
}
else {
int k = 0, t = i / 3 * 3 + j / 3;
int l = 0;
for (k = 0; k < 9; k++) {
l = initSet[k];
if (row[i][k] != 0 || column[j][k] != 0 || square[t][k] != 0) {
continue;
}
else {
sudoku[i][j] = l;
row[i][k] = column[j][k] = square[t][k] = 1;
sign = ToNext(initSet, row, column, square, sudoku, i, j, path);
if(sign != 0){
return sign;
}
}
row[i][k] = (row[i][k] == 2) ? 2 : 0;
column[j][k] = (column[j][k] == 2) ? 2 : 0;
square[t][k] = (square[t][k] == 2) ? 2 : 0;
sudoku[i][j] = 0;
}
}
return sign;
}
int ToNext(int *initSet, int **row, int **column, int** square, int **sudoku, int i, int j, char *path) {
int sign = 0;
if (j == 8) {
if (i == 8) {
if (mode == 'c') {
sign = MixSet(CreateSet(8), 0, CreateSet(8), sudoku, CreateArray());
}
else {
FileOutput(path, sudoku);
sign = -2;
}
if (sign == 0)
return -2;
}
else {
sign = GenerateSudokus(initSet, row, column, square, sudoku, i + 1, 0, path);
}
}
else {
sign = GenerateSudokus(initSet, row, column, square, sudoku, i, j + 1, path);
}
return sign;
} - 生成映射集合
int MixSet(int *mixSet, int i, int *set, int **puzzle, int **out) {
int j = 0, sign = 0;
for (j = 0; j < 8; j++) {
if (set[j] != 0) {
continue;
}
mixSet[i] = j + 1;
set[j] = 1;
if (i == 7) {
sign = Mix(puzzle, mixSet, out);
}
else {
sign = MixSet(mixSet, i + 1, set, puzzle, out);
}
if (sign == -1)
return sign;
set[j] = 0;
}
return sign;
}
- 对初始数独进行映射
int Mix(int **puzzle, int *minSet, int **out) {
int i = 0, j = 0;
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
if (puzzle[i][j] == 9) {
out[i][j] = puzzle[i][j];
}
else {
out[i][j] = minSet[puzzle[i][j]-1];
}
}
}
n++;
FileOutput("sudoku.txt", out);
if (n >= N) {
DeleteArray(out);
return -1;
}
return 0;
}
实际时间
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| 30 | 30 | ||
| Development | 开发 | 690 | 1080 |
| 150 | 180 | ||
| 60 | 40 | ||
| 30 | 50 | ||
| 60 | 30 | ||
| 120 | 180 | ||
| 90 | 240 | ||
| 60 | 240 | ||
| 120 | 120 | ||
| Reporting | 报告 | 180 | 240 |
| 90 | 120 | ||
| 30 | 60 | ||
| 60 | 60 | ||
| Sum | 合计 | 900 | 1350 |
总结
- 编程基础太差:
- Bug具有反复性,仍然会出现与"==","||"相关的错误
- 逻辑不清晰,回溯法仍然需要大量的调试才能正确
- 时间规划不合理,前期准备工作太多,留给具体代码实现和后期测试的时间不够充足。
- 没有充分的参考资料和进行调查,以至于高估了方案的可行性
- 基本没有运用面向对象课程中学习的内容

