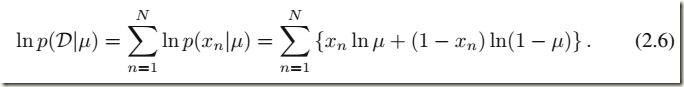2.1 Binary variables 二元变量分布_PRML模式识别与机器学习读书笔记
Bernouli 分布
单变量x ∈{0, 1} ,x的概率由参数 μ,表示:
统一格式,有:
Bernouli 分布,期望与方差:
对于x的观察数据集 ![]() ,似然函数是 μ 的函数,假定 xi 之间独立,有:
,似然函数是 μ 的函数,假定 xi 之间独立,有:
从频率论角度,我们可以用最大化似然函数的方法(等价于最大化ln函数)来评估 μ 值,似然函数的自然对数有:
使得 lnp(D|μ)=0 ,得到μ 的最大似然估计:
也即是样本均值,x=1的个数为m,则:
对于仍硬币实验,总共仍了3次,且出现的都是正面,那么μ ML= 1,预测以后都是扔出正面了,最大似然估计造成了over-fitting。
对于小样本集更容易引起该问题,后面会介绍引入μ 的先验概率有助于得到更合理的结果。
binomial distribution
我们来看N个样本中x=1 的个数m的分布情况,这就是binomial distribution二项式分布了:
期望和方差:
下图是m=10,μ=0.25的分布:
2.1.1 Beta distribution
gamma函数
首先来复习一下gamma函数:
有如下递归性质:
Γ(x+1)=xΓ(x)
由此容易得到:
Γ(n)=(n−1)!
我们在看一下Beta函数:
有:
Gamma函数在概率统计中使用非常广泛,在很多重要的分布,如t分布,χ2 分布,F 分布,Beta分布, Dirichlet 分布中都有它的影子。最直接的还是Gamma分布,由gamma函数变形:
得到Gamma分布最简单形式的密度函数:
做一个变换 x=βt,这样就得到Gamma分布普遍形式:
α :shape parameter, 主要决定了分布曲线的形状;
β: rate parameter ,inverse scale parameter (1/β 称为scale parameter),主要决定曲线有多陡。
回到主题。前面我们说到Bernouli 分布在小数据集上使用最大似然法会出现overfitting,因此从贝叶斯理论出发,我们需要一个先验概率p(μ)。
如何选取先验概率的分布?似然函数与μx(1-μ)1-x 成正比,我们希望先验也有类似的性质,这样后验概率(先验与似然函数的乘积)也会存在相似的结构,这种结构的先验概率称为共轭性:
Conjugate Prior: In Bayesian probability theory, if the posterior distributions p(θ|x) are in the same family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood. ----from wiki
在贝叶斯统计理论中,如果某个随机变量Θ的后验概率 p(θ|x)和气先验概率p(θ)属于同一个分布簇的,那么称p(θ|x)和p(θ)为共轭分布,同时,也称p(θ)为似然函数p(x|θ)的共轭先验。
这里我们采用beta 分布作为先验:
上式中的系数保证分布的归一化,即使的:
期望与方差:
beta分布取不同a,b值的分布:
μ 的后验分布由二项分布的似然函数2.9式与先验相乘并归一化,有下面的形式:
其中l=N-m,归一化可以参考2.13式得到系数,确切的概率:
这又是一个beta分布,a和b分别增加了m和n,而这个后验又可以作为后续猜测的先验,最后还是得到一个beta分布。这种方式称为sequential approach, 下图是一个sequential Bayesian inference连续贝叶斯推理,前后都是beta分布;先验中a=b=2,只试验了一次,N=m=1,后验的beta参数:a=3,b=2:
而得到的分布我们可以看到会越来越sharp,因为观测的数据越多,不确定性也就是越来越小了。
如上面的beta分布图我们可以看到,a,b越大,图形越来越sharp,方差也就越来越小了。
假如我们要预测下一次实验的结果,也就是给定现有实验数据D,得到下次预测的分布:
结合2.15 beta分布的均值公式,得到:
可以看出,当m,n趋于无穷时,结果逼近最大似然结果,这也是一个普遍性质:贝叶斯与最大似然方法基于无限大数据集的结果是一致的。