P-Value P值的含义
p值是在假定原假设为真时，得到与样本相同或者更极端的结果的概率。
如果是检验问题，p值反映的是样本数据支持原假设的证据，p值越大，证据越强。
p值就是在原假设下，该总体出现现有数据的概率，或者说在现有数据下，原假设成立的一种合理性，p值越大，原假设成立的可能性就越大。
p值越少，就说明原假设成立的可能性越小。通常当p值小于0.05时，就认为原假设不成立。
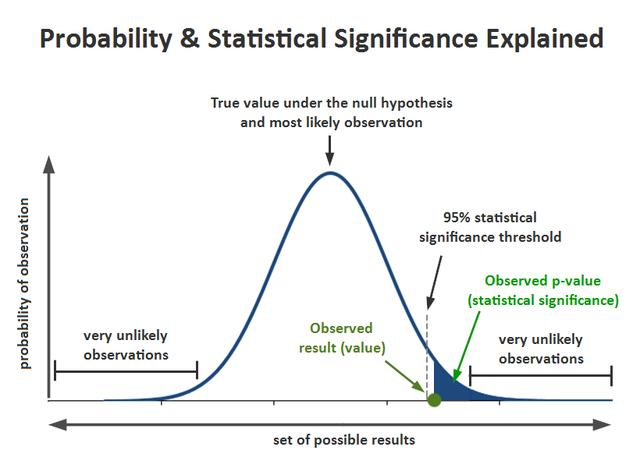
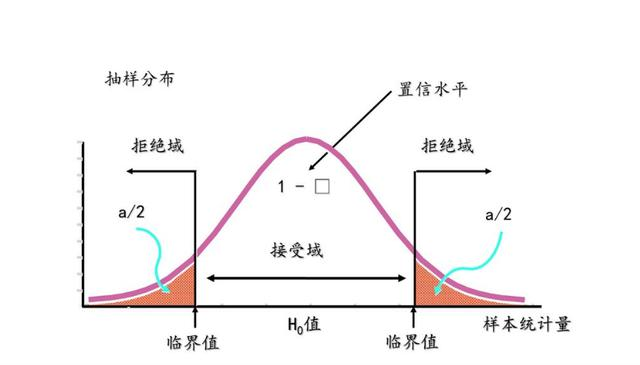
P值就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。如果P值很小，说明这种情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，P值越小，我们拒绝原假设的理由越充分。
总之，P值越小，表明结果越显著。但是检验的结果究竟是“显著的”、“中度显著的”还是“高度显著的”需要我们自己根据P值的大小和实际问题来解决。
为了检验原假设，我们需要专门构造一个检验统计量,并计算p值。在原假设成立的条件下，我们能够得到检验统计量的理论分布。通过将样本检验统计量与理论分布进行了对比获得p值。p值本身就是一个样本统计量,它给出了在假设是真实的情况下，拒绝原假设的概率。
让我们假定有效推断的条件已经满足，当观察到一个很小的p值(例如0.05、0.01，或者0.001)，我们知道下面的两件事之一一定是真实的:
要么在原假设是真实的假设下，小概率事件发生了;
要么原假设是错误的，小的p值会让我们拒绝原假设。
进而我们说研究结果是在统计上显著的。一些结果是统计显著的并且有意义，但另一些结果是统计显著的但没有意义。
在传统的应用研究中,我们追求具有很小p值的统计量。我们定义原假设的，其目的就是要拒绝它。在寻找组间差异时,我们会设定的原假设是组间没有差异，在研究变量之间的关系时，我们设定的原假设是变量间相互独立。然后我们收集数据来拒绝原假设，当收集到充足的数据后,检验过程是有统计功效的。
P值就是当原假设为真时，比所得到的样本观察结果更极端的结果出现的概率。
关键词：p值，P-Value，含义，意义，理解
