【实数系统】 04 - 连分数
我们一直在不自觉地使用着十进制小数(decimal fraction)表示实数,小数运算方便、容易理解,让实数使用起来更加自如。但小数却不能提供更多关于实数本身的性质,尤其是对无理数、超越数的研究,小数表示完全无法胜任。有人会感到困惑,什么叫实数本身的性质?实数本身还有什么需要进一步研究的?比如说吧,无理数周边的有理数是如何分布的?超越数和其它无理数有什么本质区别?这些问题的回答都超出了本篇的范围,但我觉得可以从一个简单的入口来洞悉里面的世界,为今后的学习提供工具和精神上的准备。
1. 一般连分数
在正式给出定义之前,先来欣赏一下下面漂亮的表达式:
\(\sqrt{2}+1=2+\cfrac{1}{2+\cfrac{1}{2+\cdots}}\)
\(\dfrac{\sqrt{5}+1}{2}=1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}\)
\(\dfrac{4}{\pi}=1+\cfrac{1^2}{2+\cfrac{2^2}{2+\cfrac{3^2}{2+\cfrac{4^2}{\cdots}}}}\)
\(\dfrac{e-1}{e+1}=\cfrac{1}{2+\cfrac{1}{6+\cfrac{1}{10+\cfrac{1}{14+\cdots}}}}\)
\(\sqrt{a^2+b}=a+\cfrac{b}{2a+\cfrac{b}{2a+\cfrac{b}{2a+\cdots}}}\)
这里要介绍的就是连分数(Continued Fractions),它是实数的另一种表示方法,在数论等学科中有着很惊奇的应用。简单说连分数就是具有以下左边形式的表达式,其中\(a_i,b_i\)可以是任何数(甚至复数),省略号可以是有限或无穷的。右边的表达式叫一般连分数,如果\(a_0\)为整数、\(a_k(k>0)\)为正整数,它又叫简单连分数,本篇只介绍一般连分数和简单连分数。
\[a_0+\cfrac{b_0}{a_1+\cfrac{b_1}{a_2+\cdots}};\quad\quad a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\cdots}}\]
这种书写方式虽然直观,但稍显繁琐,我们可以把一般连分数写成\([a_0,a_1,a_2,\cdots]\)。值得一提的是,有限连分数显然都是一个数,但无限连分数却还只是个记号,它能不能表示数还需要进一步的结论。另外,\(s_k=[a_0,a_1,\cdots,a_k]\)称为连分数的节,\(r_k=[a_k,a_{k+1},\cdots]\)称为连分数的余式,显然有下式成立:
\[[a_0,a_1,a_2,\cdots]=[a_0,a_1,\cdots,a_{k-1},r_k]\tag{1}\]
显然连分数的每个节\(s_k\)都可以展开为一般的分数形式\(\dfrac{p_k}{q_k}\),它称为连分数的渐进分数(convergents),由数学归纳法可以推得如下公式。其中\(p_{-2},p_{-1},q_{-2},q_{-1}\)是补充进来的,它们可以使公式统一。这个公式非常漂亮,\(p_k,q_k\)居然独立地只与\(a_k\)相关,它是连分数理论的基本公式。
\[p_k=a_kp_{k-1}+p_{k-2};\quad (p_{-2}=0,p_{-1}=1)\tag{2}\]
\[q_k=a_kq_{k-1}+q_{k-2};\quad (q_{-2}=1,q_{-1}=0)\]
直觉可能已经告诉你,渐进分数可能是实数的一种逼近序列,研究渐进分数之间的关系就能知道这个逼近的趋势。将上式分别乘上\(q_{k-1},p_{k-1}\)并相减得到\(p_kq_{k-1}-q_kp_{k-1}=p_{k-2}q_{k-1}-q_{k-2}p_{k-1}\),迭代计算得到公式(3),并进而有公式(4),用类似的方法和已有结论容易有公式(5)(6)。它们都表示了渐进分数的逼近情况,以后会经常用到。
\[q_kp_{k-1}-p_kq_{k-1}=(-1)^k\tag{3}\]
\[\dfrac{p_{k-1}}{q_{k-1}}-\dfrac{p_k}{q_k}=\dfrac{(-1)^k}{q_kq_{k-1}}\tag{4}\]
\[q_kp_{k-2}-p_kq_{k-2}=(-1)^{k-1}a_k\tag{5}\]
\[\dfrac{p_{k-2}}{q_{k-2}}-\dfrac{p_k}{q_k}=\dfrac{(-1)^{k-1}a_k}{q_kq_{k-2}}\tag{6}\]
你可能注意到,余式\(r_k\)完全可以当做\(a_k\)看待,所以可以有表达式(7)。这个表达式将余式和连分数的值联系了起来,对研究逼近很有用处。另外,结合公式(2)很容易得到以下有趣的表达式(8)。它们不仅漂亮,对今后的证明也都很有用。
\[[a_0,a_1,a_2,\cdots]=\dfrac{p_{k-1}r_k+p_{k-2}}{q_{k-1}r_k+q_{k-2}}\tag{7}\]
\[\dfrac{p_k}{p_{k-1}}=[a_k,a_{k-1},\cdots,a_0];\quad \quad \dfrac{q_k}{q_{k-1}}=[a_k,a_{k-1},\cdots,a_1]\tag{8}\]
2. 简单连分数
以上的讨论都是针对一般连分数进行的,得出的结论也都是关于表达式形式的。如果想得到关于值的性质,看来必须限制\(a_k\)的值,现在就假设\(a_k\)为正数(比简单连分数条件弱一些)。由公式(4)可知偶(奇)数项渐进分数是递增(减)的,而且奇数项皆大于偶数项。从图像上看感觉就是两条逐渐靠近的曲线,我们自然会问:它们会收敛于同一个值吗?对于有限连分数,答案是显然的,最后一项会等于分数值。但对于无限连分数,极限的知识告诉我们它们不一定相遇,所以还需要研究它们相遇的条件。
首先,渐进分数序列收敛时称连分数是收敛的,它本质上是说两条曲线收敛于同一值,该值称为连分数的值。容易看出连分数收敛和它的余式收敛是等价的,那么无穷连分数收敛的条件是什么呢?由公式(4)可知收敛的等价条件是\(q_kq_{k+1}\to+\infty\),下面来证它的充要条件是\(\sum{a_k}\)发散。先证必要性,即由极限为无穷证明级数发散。首先容易有\(q_k>q_{k-2}\),从而\(q_k>q_{k-1},q_{k-1}>q_{k-2}\)有一个成立,结合公式(2)可有\(q_k<\dfrac{1}{1-a_k}q_{k-1}\)或\(q_k<\dfrac{1}{1-a_k}q_{k-2}\)。如果级数收敛,由级数理论可知\(\prod\limits_{k=0}^\infty{(1-a_k)}\)有非零值,从而\(q_k\)有限,与极限为无穷矛盾,所以级数必收敛。再证充分性,即由级数发散可证极限为无穷。现由\(q_k\geqslant q_{k-2}+ca_k\)分别对奇偶项进行估值,合并有\(q_k+q_{k+1}>c\sum\limits_{i=0}^k{a_i}\),然后很容易有\(q_kq_{k+1}\to+\infty\)。证明完成。
可以猜想,不同的连分数可能收敛到同一个实数,这样实数的连分数表示就没有唯一性。为达到唯一性,并获得更多的结论,从现在开始我们仅讨论简单连分数,并简称为连分数。连分数的\(a_k\)称为局部商(partial quotient),\(a_0\)可为负数,为保持结论的处处成立,我们再限定它必须非负,这并不影响结论对所有连分数的适用性。另外,对有限连分数有\([a_0,\cdots,a_{n-1},1]=[a_0,\cdots,a_{n-1}+1]\),连分数表示仍然不唯一,但容易证明,如果限制\(a_n>1\),则实数有唯一的连分数表示(十进制小数表示也要剔除掉\(\dot{9}\)才有唯一表示)。
比较自然地可以想到,实数的唯一连分数表示可以用类似辗转相除的方法逐步得到。每次\(a_k\)取余式\(r_k\)的整数部分,余式的小数部分取倒数得到新的余式\(r_{k+1}\),依次类推,比如由下表可得到\(\pi=[3,7,15,1,292,1,\cdots]\)。显然有理数在有限步后余式为0,结束流程得到有限连分数,而无理数则会一直进行下去,得到无限连分数。
| \(r_0=3.1415926\) | \(r_1=7.0625\) | \(r_2=15.99659\) | \(r_3=1.0034\) | \(r_4=292.634\) | \(r_5=1.575\) |
| \(a_0=3\) | \(a_1=7\) | \(a_2=15\) | \(a_3=1\) | \(a_4=292\) | \(a_5=1\) |
由公式(7)可知\(\alpha=[a_0,\cdots,a_n,r_{n+1}]=\dfrac{p_kr_{k+1}+p_{k-1}}{q_kr_{k+1}+q_{k-1}}\),其中\(a_{n+1}\leqslant r_{n+1}<a_n+1\),从而得到渐进分数的误差估计公式(9)。该误差公式可以继续得到误差比较式(10)(11),即渐进分数越来越接近连分数的值。
\[\dfrac{1}{q_k(q_k+q_{k+1})}<\left|{\alpha-\dfrac{p_k}{q_k}}\right|\leqslant\dfrac{1}{q_kq_{k+1}}\tag{9}\]
\[\left|{\alpha-\dfrac{p_{k+1}}{q_{k+1}}}\right|<\left|{\alpha-\dfrac{p_k}{q_k}}\right|\tag{10}\]
\[\left|{q_{k+1}\alpha-p_{k+1}}\right|<\left|{q_k\alpha-p_k}\right|\tag{11}\]
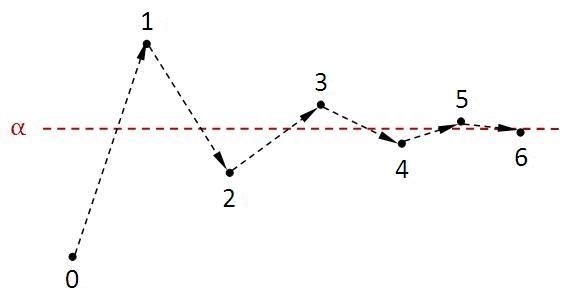
3. 逼近的度量
实数的连分数表示不依赖于进制,\(a_k\)的大小一定程度上表示了逼近的程度,它是研究无理数的有力工具。连分数的渐进分数可以由公式(2)递推得到,\(p_k,q_k\)都是整数,由公式(3)得到\(p_k,q_k\)又是互质的,所以公式(2)推导出的渐进分数都是既约分数。
关于用有理数逼近无理数,我们有这样一个基本问题:怎样用尽量小分母的分数来逼近已知无理数?这个问题不仅有实际应用价值,还能考察一个无理数的性质。首先我们可以有这样的粗略感觉,对选定的分母可有一个最逼近的分数,随着分母的递增,必然有某个分数更加逼近,然而这些分母之间可能是有间隔的。先对这样的逼近作一个明确的定义,对任意实数\(\alpha\),若既约分数\(\dfrac{n}{m}\)比任何分母不大于\(m\)的分数都更逼近\(\alpha\),\(\cfrac{n}{m}\)称为\(\alpha\)的最佳逼近。即若\(m'\leqslant m\),\(n'\)任意,则有表达式(12)。一个实数可能有很多的最佳逼近,它们分母递增,且值逐渐逼近\(\alpha\)直至收敛。
\[\left|{\alpha-\dfrac{n}{m}}\right|<\left|{\alpha-\dfrac{n'}{m'}}\right|\tag{12}\]
由前面的分析知道,渐进分数逐步靠近收敛值,而且它们的分母也逐渐增大,那它们是不是就是我们要找的最佳逼近呢?答案让人惊喜,但也有点让人失望,渐进分数都是最佳逼近,但不是所有最佳逼近都是渐进分数。在得到更细致的结论之前,我们需要引入中位数的概念。分数\(\dfrac{a+c}{b+d}\)称为\(\dfrac{a}{b}\)和\(\dfrac{c}{d}\)的中位数,容易证明它的值介于\(\dfrac{a}{b}\)和\(\dfrac{c}{d}\)之间(中位数定理)。
考察如下序列,它们和\(\dfrac{p_{k-1}}{q_{k-1}}\)之间都是中位数关系,所以这是一个单调序列,且位于收敛值的同一侧。这个序列如果再前进一步,就是\(\dfrac{p_{k-1}}{q_{k-1}}\)和\(\dfrac{p_k}{q_k}\)的中位数,同样推理,它必和\(\dfrac{p_{k-1}}{q_{k-1}}\)在同一侧。这个有趣的过程可以启发我们如何计算\(a_k\),已知前两个渐进分数和收敛值\(\alpha\)时,可以在中位数跨越\(\alpha\)时确定\(a_k\)。
\[\dfrac{p_{k-2}}{q_{k-2}},\dfrac{p_{k-2}+p_{k-1}}{q_{k-2}+q_{k-1}},\dfrac{p_{k-2}+2p_{k-1}}{q_{k-2}+2q_{k-1}},\cdots,\dfrac{p_{k-2}+a_kp_{k-1}}{q_{k-2}+a_kq_{k-1}}=\dfrac{p_k}{q_k}\]
继续回到前面的问题,现在知道渐进分数和中位数分布在收敛值的两侧,且每侧都是单调的。每侧相邻两个分数可以表示为\(\dfrac{P(r)}{Q(r)}=\dfrac{p_kr+p_{k-1}}{q_kr+q_{k-1}}\)和\(\dfrac{P(r+1)}{Q(r+1)}\),它们的差为\(\dfrac{1}{Q(r)Q(r+1)}\),分子为1表明它们之间不可能有分母大于\(Q(r+1)\)的分数,否则该分数与\(\dfrac{P(r)}{Q(r)}\)的差必然大于\(\dfrac{1}{Q(r)Q(r+1)}\)。所以最佳逼近必然只能取渐进分数及其中位数,显然渐进分数必然是最佳逼近,但中位数就不一定是了,它甚至都不一定是既约分数。
仔细比较公式(10)和(11),(11)明显比(10)更严格,如果把公式(12)也换成较严格的条件,会发生什么呢?为区别这两种逼近,满足公式(12)的称为第一类型最佳逼近,而满足公式(13)的称为第二类型最佳逼近。第二类型的最佳逼近当然肯定也是第一类型的,反之则不一定成立,第二类型将剔除掉所有中位数,得到让我们心怡的结论。
\[\left|{m\alpha-n}\right|<\left|{m'\alpha-n'}\right|\tag{13}\]
证明的重点都在于对公式(4)(9)的深度理解,相邻连分数之间再也插不进比它们分母小的分数。如果第二类型最佳逼近\(\dfrac{n}{m}\)在\(\dfrac{p_{k-1}}{q_{k-1}}\)和\(\dfrac{p_{k+1}}{q_{k+1}}\)之间,它必然在\(\dfrac{p_{k-1}}{q_{k-1}}\)和\(\dfrac{p_k}{q_k}\)之间,所以\(m>q_k\)且\(\left|{m\alpha-n}\right|<\left|{q_k\alpha-p_k}\right|<\dfrac{1}{q_{k+1}}\)。而另一方面\(\left|{\alpha-\dfrac{n}{m}}\right|\geqslant\left|{\dfrac{p_{k+1}}{q_{k+1}}-\dfrac{n}{m}}\right|\geqslant\dfrac{1}{mq_{k+1}}\),矛盾,所以第二类型逼近只能是渐进分数。反之如果\(k>s\),则利用误差估计(9)有\(\left|q_k\alpha-p_k\right|\leqslant\dfrac{1}{q_{k+1}}<q_s+q_{s+1}<\left|q_s\alpha-p_s\right|\),也就是说所有渐进分数都是第二类型逼近。所以除了特殊情况\(\alpha=x.5\)外,第二类型渐进逼近和渐进分数是等价的。
渐进分数可以寻找最佳的有理逼近,它可以被用于齿轮制造、日历编撰等,另外还可以求对数的近似值(想想怎么算?)。
渐进分数是实数的逼近表示,那么局部商\(a_i\)的大小能否说明什么呢?笼统地说,它表示渐进分数离实数究竟有多近,即可以用来度量逼近。如何度量一个有理数对实数的逼近程度?研究误差和分母的关系是一个比较可行的方法,根据公式(9)有关系式(14)。这个关系式是对所有渐进分数都成立的,欲构造单个无限接近该误差的连分数是很容易的,所以该式不能被加强。该结论有两个扩展结论:(1)相邻两个渐进分数必有一个满足(15)式;(2)相邻三个渐进分数必有一个满足(16)式。而且考察\([1,1,1,\cdots]\)可知,该结论已经不能再扩展。
\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{q_k^2}\tag{14}\]
\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{2q_k^2}\tag{15}\]
\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{\sqrt{5}q_k^2}\tag{16}\]
利用公式(9)容易得到以下估计式(17),该式说明了\(a_k\)越大,它所对应的渐进分数就“更好地”逼近连分数的值,而\([1,1,1,\cdots]\)则是最坏的数。关于逼近的度量还有很多结论,这里只是抛砖引玉,让大家有个概念,具体内容请参考相关资料。
\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{a_{k+1}q_k^2}\tag{17}\]
现在来看一个逼近度量的应用,由此窥见连分数理论在高等理论中的作用。考察\(n\)次代数数\(\alpha\),设它满足有理系数多项式\(f(x)=(x-\alpha)g(x)\)。易证\(g(\alpha)\ne 0\),取使\(g(x)\ne 0\)的区间,并设\(\left|{g(x)}\right|>M\)。在区间上讨论\(\dfrac{p}{q}-\alpha=\dfrac{f(\dfrac{p}{q})}{g(\dfrac{p}{q})}\),容易有\(\left|{\dfrac{p}{q}-\alpha}\right|>\dfrac{1}{Mq^n}\)。进一步讨论既有刘维尔(Liouville)定理:对\(n\)次代数数\(\alpha\),存在正数\(C\)使得(18)式总成立。该定理指出了代数数的有理逼近性质,可以用它来轻松构造超越数(取适当\(a_k\)),刘维尔用它构造了第一个超越数\(\sum\limits_{k=1}^\infty{10^{- k!}}\)。
\[\left|{\alpha-\dfrac{p}{q}}\right|>\dfrac{C}{q^n}\tag{18}\]
4. 循环连分数
十进制循环小数是有理数,你可能好奇循环(periodic)连分数会有什么性质呢?首先,模仿循环小数,我们把循环连分数记作\([a_0,\cdots,a_{s-1},\dot{a}_s,a_{s+1},\cdots,\dot{a}_k]\)。对于循环连分数,在进入循环节后总有\(r_k=r_{k+l}\),容易由归纳式得到一个二次方程,并进而知道该连分数是2次代数数。反过来,2次代数数的连分数,也必然是循环的,这个定理最初由拉格朗日证明。大概思路是考察余式的二次方程,发现它的系数有界,从而余式的个数有限,所以必然会出现循环。这里打算从另一个角度来证明这个定理,因为我们可以得到更多有趣的东西。
我们先从最简单的情况开始考虑,连分数\(\alpha=[\dot{a}_0,\cdots,\dot{a}_n]\)称为纯循环连分数,并记\(\beta=[\dot{a}_n,\cdots,\dot{a}_0]\)。考察由归纳公式形成的二次方程,并使用公式(8),容易证明\(\alpha\)和\(\overline{\alpha}=-\dfrac{1}{\beta}\)是同一整系数二次方程的根,它们互为共轭且满足条件(19)。容易知道二次代数数都有形式\(r+s\sqrt{D}\),满足(19)的二次代数数称为既约的。可以证明\(\alpha\)的余式\(r_1\)也是即约的,也容易知道对某个\(D\)即约二次代数数是有限的,故必有某个余式满足\(r_k=\alpha\),这就证明了即约二次代数数必是纯循环连分数。综合得到纯循环连分数和即约二次代数数是等价的。对于一般的二次代数数,用\(\alpha\)的表达式来表示\(r_k\),可以证明它迟早会成为即约的,所以循环节必将出现,故循环连分数和二次代数数也是等价的。
\[\alpha>1,\quad -1<\overline{\alpha}<0\tag{19}\]
容易证明\(\alpha=\sqrt{D}+a_0\)是即约的(\(a_0\)为\(\sqrt{D}\)的首项),记\(\alpha=[\dot{2a}_0,\cdots,\dot{a}_n]\)。由以上结论可有\(\beta=-\dfrac{1}{\overline{\alpha}}=[\dot{a}_n,\cdots,\dot{2a}_0]\),而\(\beta=\dfrac{1}{\alpha-2a_0}=[\dot{a}_1,\cdots,a_n,\dot{2a}_0]\),所以\(a_1,\cdots,a_n\)对称。故有\(\alpha=[\dot{2a}_0,a_1,a_2,\cdots,a_2,\dot{a}_1]\),进而有表达式(20)。
\[\sqrt{D}=[a_0,\dot{a}_1,a_2,\cdots,a_2,a_1,\dot{2a}_0]\tag{20}\]
【全篇完】



 浙公网安备 33010602011771号
浙公网安备 33010602011771号