《线性代数》随笔:学以致用
线性代数就是把一组数通过线性组合得到另一组数。所谓的线性组合,就像买菜一样,我可以买半斤青菜、两根胡萝卜还有一棵西兰花――都是把每种菜乘上一个常数最后加起来算个总账。我绝不会说我要买青菜乘上萝卜、或者西兰花除以两斤青菜。菜和菜之间的乘除是毫无意义的。所以买菜就是一种线性组合。
我之前说到过,我是因为工作上写程序要用到才去重新学习了线性代数。这其中所涉及的问题其实大家在高中就经常做这类的题目,就是坐标变换。在数学家的眼里,所有的几何图形都是数字或公式。这其中最基本的就是点,而平面上的点就可以用两个数:X坐标和Y坐标表示,空间里的点只要多一个Z坐标就可以精确地表示了。点可以构成线、构成面、构成体,要表示一个物体的,只要给出足够多的关键点的坐标就可以了。
用数来表示点的目的自然是要用数的计算来表示点的关系了,经过总结和分析,刚体的运动都分解成为位移和旋转的组合。
比如小明从家到学校的线路从家里出门开始,可以分解为:
1. 向前100米
2. 左转90度
3. 向前50米
4. 右转90度
5. 向前50米
6. 左转45度
7. 向前200米到达学校
幸运的是,坐标的变换可以表示成为坐标的线性组合。也就是说,从原坐标到新坐标只要乘上一个矩阵就可以了。
二维坐标位移和旋转的基本变换矩阵是现成的:
位移:
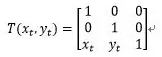
旋转:

为什么计算二维坐标要用三阶矩阵呢?那是因为位移变换要给每一个坐标分量都加上一个常数,而在2阶矩阵里每一项最终都会和x或者y相乘,不会有独立的常数存在。解决方法很简单,把二维坐标增加一维,变成(x, y, 1),这样乘出来的结果里就有一个会和1相乘,也就允许常数项存在了。有了基本矩阵,任何复杂的变换就可以写成一系列矩阵相乘了。
现在我们再来看小明到学校的路,如果以小明家的坐标为原点,面向Y轴正方向前进,那学校的坐标就可以表示为:
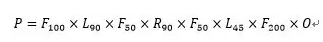
其中O是原点坐标,Fxxx是前进矩阵,Rxx是右转矩阵,Lxx是左转矩阵。
到了三维空间,以上结论同样成立,只不过矩阵变成了4阶,并且旋转矩阵包含更多信息。因为不同于二维平面只有维一一根转轴,三维空间里任意直线都可以成为转轴,所以三维旋转矩阵里还包含了转轴方向的内容。
三维空间的情况的稍微复杂一些。联想体操和跳水比赛的动作解说,又是向前向后翻腾,又是转体,这其实就是运动员绕不同转轴在旋转。跳水也许不是一个好的例子,因为人体能屈能伸,所以不是刚体。
我们可以想像有一根筷子也想来体验跳水这项运动,它是名符其实的刚体,它选择的动作是向前翻腾3周半,接转体270度,再接向后翻腾2周最后落到地上,那它落地的时候是头朝地还是脚朝地呢?
这个脑洞大开的题目要是用坐标变换去解,只需将筷子初始方向写成一个矩阵,再乘上三个旋转矩阵马上就可以得到答案。
三难空间的坐标变换另一个重要的应用就是计算机三维图形了,这也是我工作涉及的内容以及我学习线性代数的源动力。我们在3D游戏里看到的所有的东西,都是计算机程序将数以万计的基本图形(三角形)通过坐标变换显示在二维屏幕上的,而这些坐标变换无一不是由矩阵相乘来实现。你没看错,坐标变换还可以把三维图形转换成为二维图形。这个变换矩阵称为投影矩阵,它的名称和原理都来自于实现世界中光照到物体上投到地上或墙上的影子,这叫作正投影。另有一种更加常用的投影方式可以在屏幕上投影出近大远小的效果,叫作透视投影。
除了位移、旋转和投影矩阵外,计算机还用到了一个缩放矩阵,把三维图形放大缩小,这样游戏中同样的东西,大小不同就不需要做两份了。三角形和四种基本矩阵一起,构成了我们在屏幕上所看到了纷繁复杂的三维虚拟世界。
如果只是这样,坐标和矩阵乘一乘就好了,纯粹体力活,不会引起我啃数学书的兴趣。真正吸引我的是这个过程的逆向过程。我们已经能接受了屏幕是二维的,计算机只要把三维图形乘上一个由程序员指定的矩阵就可以不费力地显示在屏幕上。可是事情还没完,用户的鼠标输入也是二维的,鼠标在屏幕上点击了一下计算能得到这个屏幕上点的二维坐标,可是怎么才能知道这个二维点对应的是三维世界里的哪一个物体呢?是让程序员再指定一个反向的矩阵么?好像不实现,因为程序员也不知道这个矩阵是什么,就算知道,以我们心性也绝对懒得去做。怎么办?读书去!
于是就有了这个随笔系列,前一篇已经讲了,对于任意一个矩阵乘法:

都可以找到一个M的逆矩阵或者叫倒数,使得:
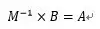
只要求出所有正向矩阵乘积的逆矩阵就可以。哇,天才啊!
《线性代数》随笔系列首发于微信公众号:龙猫图书馆,这是由猫馆长发起的小资文艺青年聚集之所,欢迎关注。