剑指Offer面试题:9.二进制中1的个数
一、题目:二进制中1的个数
题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
二、可能引起死循环的解法
一个基本的思路:先判断整数二进制表示中最右边一位是不是1。接着把输入的整数右移一位,此时原来处于从右边数起的第二位被移到最右边了,再判断是不是1。这样每次移动一位,直到整个整数变成0为止。
怎么判断一个整数的最右边是不是1:只要把整数和1做位与运算看结果是不是0就知道了。
public static int NumberOf1Solution1(int n) { int count = 0; while (n > 0) { if ((n & 1) == 1) { count++; } n = n >> 1; } return count; }
PS:右移运算符m>>n表示把m右移n位。右移n位的时候,最右边的n位将被丢弃。如果数字原先是一个正数,则右移之后在最左边补n个0;如果数字原先是负数,则右移之后在最左边补n个1。例如下面对两个八位二进制数进行右移操作:
00001010>>2=00000010
10001010>>3=11110001
那么,问题来了:上面的方法如果输入一个负数,比如0x80000000,如果一直做右移运算,最终这个数字就会变成0xFFFFFFFF而陷入死循环。
三、避免引起死循环的解法
为了避免死循环,我们可以不右移输入的数字i:
(1)首先把i和1做与运算,判断i的最低位是不是为1。
(2)接着把1左移一位得到2,再和i做与运算,就能判断i的次低位是不是1。
(3)这样反复左移,每次都能判断i的其中一位是不是1。
public static int NumberOf1Solution2(int n) { int count = 0; uint flag = 1; while (flag >= 1) { if ((n & flag) > 0) { count++; } flag = flag << 1; } return count; }
PS:这个解法中循环的次数等于整数二进制的位数,32位的整数需要循环32次。
四、高效新颖的解法
把一个整数减去1,再和原整数做与运算,会把该整数最右边一个1变成0。那么一个整数的二进制表示中有多少个1,就可以进行多少次这样的操作。

public static int NumberOf1Solution3(int n) { int count = 0; while (n > 0) { count++; n = (n - 1) & n; } return count; }
PS:把一个整数减去1之后再和原来的整数做位与运算,得到的结果相当于是把整数的二进制表示中的最右边一个1变成0。很多二进制的问题都可以用这个思路解决。
五、单元测试
5.1 测试用例
// 输入0,期待的输出是0 [TestMethod] public void NumberOfOneInBinaryTest1() { Assert.AreEqual(BinaryHelper.NumberOf1Solution2(0),0); Assert.AreEqual(BinaryHelper.NumberOf1Solution3(0),0); } // 输入1,期待的输出是1 [TestMethod] public void NumberOfOneInBinaryTest2() { Assert.AreEqual(BinaryHelper.NumberOf1Solution2(1), 1); Assert.AreEqual(BinaryHelper.NumberOf1Solution3(1), 1); } // 输入10,期待的输出是2 [TestMethod] public void NumberOfOneInBinaryTest3() { Assert.AreEqual(BinaryHelper.NumberOf1Solution2(10), 2); Assert.AreEqual(BinaryHelper.NumberOf1Solution3(10), 2); } // 输入0x7FFFFFFF,期待的输出是31 [TestMethod] public void NumberOfOneInBinaryTest4() { Assert.AreEqual(BinaryHelper.NumberOf1Solution2(0x7FFFFFFF), 31); Assert.AreEqual(BinaryHelper.NumberOf1Solution3(0x7FFFFFFF), 31); } // 输入0xFFFFFFFF(负数),期待的输出是32 [TestMethod] public void NumberOfOneInBinaryTest5() { Assert.AreEqual(BinaryHelper.NumberOf1Solution2(0xFFFFFFFF), 32); Assert.AreEqual(BinaryHelper.NumberOf1Solution3(0xFFFFFFFF), 32); } // 输入0x80000000(负数),期待的输出是0 [TestMethod] public void NumberOfOneInBinaryTest6() { Assert.AreEqual(BinaryHelper.NumberOf1Solution2(0x80000000), 0); Assert.AreEqual(BinaryHelper.NumberOf1Solution3(0x80000000), 0); }
5.2 测试结果
(1)测试通过情况:
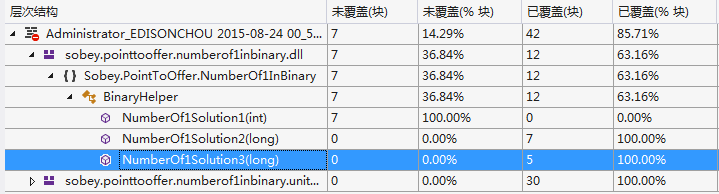
(2)代码覆盖率:


 题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。一个基本的思路:先判断整数二进制表示中最右边一位是不是1。接着把输入的整数右移一位,此时原来处于从右边数起的第二位被移到最右边了,再判断是不是1。这样每次移动一位,直到整个整数变成0为止。
题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。一个基本的思路:先判断整数二进制表示中最右边一位是不是1。接着把输入的整数右移一位,此时原来处于从右边数起的第二位被移到最右边了,再判断是不是1。这样每次移动一位,直到整个整数变成0为止。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix