编程之美扫雷篇
一、编程之美扫雷篇
这是我几年前在人人网上写的文章,转到这里来。
从师兄那里得到了一本很好玩的书《编程之美》,爱不释手。其中有一道扫雷的趣题书中没有给出答案,原题是这样的:

问题一:当这个游戏有40个地雷没有被发现的时候,A、B、C三个方块有地雷的概率P(A),P(B),P(C)各是多少??
问题二:这个游戏局面一共有16*16=256个方块,P(A),P(B),P(C)的相互大小关系和当前局面中地雷总数有联系么?比如,当地雷总数从10个逐渐变化到240个,P(A),P(B),P(C)的三条曲线是如何变化的?它们会不会相交?
第一眼看上去问题很奇怪,概率怎么会和总雷数有关系呢?牛人任晓祎在他的博客中http://snarc.ia.ac.cn/ren/html/y2010/390.html给出了一个解答。但是他的推导过程是一次性的给出了一个一般解,普通人很难做到这样,所以这里先从特殊情况开始考虑。


在图一和图二中,P(A)的概率是相等的吗?换句话说,P(A)的概率和局面的总雷数有关系吗?设总雷数为N,棋盘大小为M(这里M=25),图中可能出现的布局总数有C(M-9,N-1 )*C(8,1) 种,其中A点有雷的布局总数有C(M-9,N-1)*C(1,1) 种。
所以P(A)= (M-9,N-1)*C(1,1) / [C(M-9,N-1 )*C(8,1) ]=1/8 ,即P(A)的概率和局面的总雷数无关。下面进行下一步讨论。

在图三和图四中,P(A)的概率是相等的吗?这时图中雷的布局分成了两种情况。 这里M=30
第一种:在中间3*4的范围内有一颗雷。
第二种:在中间3*4的范围内有二颗雷。
情况一:
所有的布局总数有C(M-12,N-1) *C(4,1) 种,其中A点有雷的总数有0种。
情况二:
所有的布局总数有C(M-12,N-2) *C(3,1) *C(3,1) 种,其中A点有雷的总数有C(M-12,N-2)*C(1,1) *C(3,1) 种。
所以P(A)= C(M-12,N-2 )*C(1,1) *C(3,1) / [ C(M-12,N-2) *C(3,1) *C(3,1) ]
从上式可以看出P(A)和总雷数N有关系,下图是P(A)和总雷数N的曲线
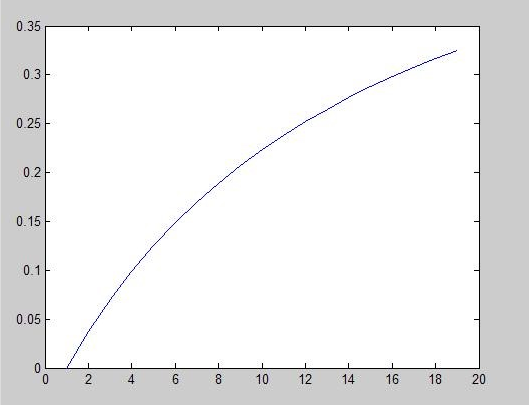
为什么这一次的概率会和总雷数相关呢?问题就在于中间的3*4的方块中的雷数不确定。按照这个思路,题目中的问题就迎刃而解了。
二、扫雷加强版
这个程序是我去年初学C语言Windows api编程时写的练手程序。当时从网上下载的杨力祥老师的教学视频,一边看一边写扫雷,收获非常大,推荐想学C Windows编程的朋友去看看。
游戏截图:

游戏中我对原来的windows扫雷进行了一点改进,每个方格内最多有两个雷,让玩家有一点新鲜感,同时也修复了原来windows扫雷计时器的bug。游戏可以在文章第一行的链接下载,不过这个程序我写的非常乱,一坨狗屎,bug非常多,后来想去debug发现难度比较大,就一直没去管它,此处就不提供源代码了。
三、扫雷++
debug不如重构。扫雷++是我最近写的一个游戏,比上一版改进了很多,玩法也完全不同于windows扫雷。游戏有点像扫雷的逆向思维过程,游戏说明如下:
1、点击任意方格可以把它变成地雷。
2、每一个字母代表一个数字,当这个数字等于周围的雷数时,字母显示为彩色。
3、所有地雷随机分布,有雷的方格随机显示一个数字
4、胜利条件:剩余雷数==0,所有字母为彩色。
你需要推理出每一个字母代表的数字,用最少的步数找到所有地雷。麻雀虽小,五脏俱全,游戏和源程序的下载在文章的第一行,由VS2005编写。
游戏截图:




