[Leetcode] Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

 

The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

最笨的办法，暴力算，果然超时了！

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int minHeight;
        int maxArea = 0, area;
        for (int i = 0; i < height.size(); ++i) {
            minHeight = height[i];
            for (int j = i; j < height.size(); ++j) {
                minHeight = (minHeight < height[j]) ? minHeight : height[j];
                area = minHeight * (j - i + 1);
                maxArea = (maxArea > area) ? maxArea : area;
            }
        }
        return maxArea;
    }
};

下面是重点， 可以通过两个栈来保存之前的信息，以减少比较次数，经典就是经典啊。我们要维护两个栈，要注意的是栈中的节点的高度一定是比当前节点小的，若发现height栈顶元素比当前元素大，则要将其出栈，同时计算面积。还有一点要注意的是处理完所有元素后若栈不为空，那么这些元素肯定是从idx延伸到最后的，还要计算其面积。

Actually, we can decrease the complexity by using stack to keep track of the height and start indexes. Compare the current height with previous one.

Case 1: current > previous (top of height stack)
Push current height and index as candidate rectangle start position.

Case 2: current = previous
Ignore.

Case 3: current < previous
Need keep popping out previous heights, and compute the candidate rectangle with height and width (current index - previous index). Push the height and index to stacks.

(Note: it is better use another different example to walk through the steps, and you will understand it better).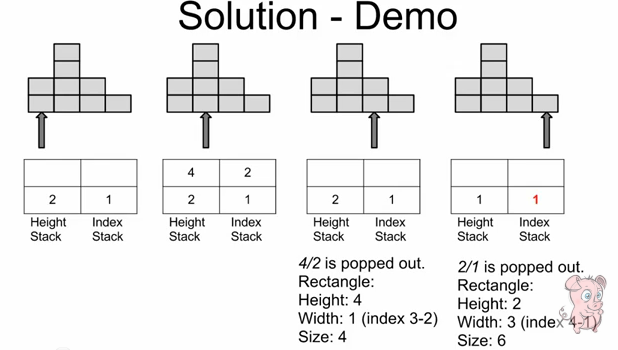

 

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int n = height.size();
        stack<int> stkHeight;
        stack<int> stkIdx;
        int maxArea = 0, tmpArea;
        int tmpHeight, tmpIdx;
        for (int i = 0; i < n; ++i) {
            if (stkHeight.empty() || height[i] > stkHeight.top()) {
                stkHeight.push(height[i]);
                stkIdx.push(i);
            }
            else if (height[i] < stkHeight.top()) {
                //tmpIdx = 0;
                while (!stkHeight.empty() && height[i] <= stkHeight.top()) {
                    tmpHeight = stkHeight.top();
                    stkHeight.pop();
                    tmpIdx = stkIdx.top();
                    stkIdx.pop();
                    tmpArea = tmpHeight * (i - tmpIdx);
                    maxArea = (maxArea > tmpArea) ? maxArea : tmpArea;
                }
                stkHeight.push(height[i]);
                stkIdx.push(tmpIdx);
            }
        }
        while (!stkHeight.empty()) {
            tmpHeight = stkHeight.top();
            stkHeight.pop();
            tmpIdx = stkIdx.top();
            stkIdx.pop();
            tmpArea = tmpHeight * (n - tmpIdx);
            maxArea = (maxArea > tmpArea) ? maxArea : tmpArea;
        }
        return maxArea;
    }
};

 上面的代码太臃肿了，可以简化如下：

class Solution {
public:
    int largestRectangleArea(vector<int> &line) {
        if (line.size() < 1) return 0;
        stack<int> S;
        line.push_back(0);
        int maxArea = 0, tmpArea;
        for (int i = 0; i < line.size(); ++i) {
            if (S.empty() || line[i] > line[S.top()]) {
                S.push(i);
            } else {
                int idx = S.top();
                S.pop();
                tmpArea = line[idx] * ((S.empty() ? i : i - S.top() - 1));
                maxArea = (maxArea > tmpArea) ? maxArea : tmpArea;
                --i;
            }
        }
        return maxArea;
    }
};