【转】地图投影系列介绍（三）_ 地图投影

4、地图投影

    4.1 投影实质

        将地球椭球面上的点映射到平面上的方法，称为地图投影。

        为什么要进行投影？            

　　　　– 地理坐标为球面坐标，不方便进行距离、方位、面积等参数的量算。            

　　　　– 地球椭球体为不可展曲面。            

　　　　– 地图为平面，符合视觉心理，并易于进行距离、方位、面积等量算和各种空间分析。

        

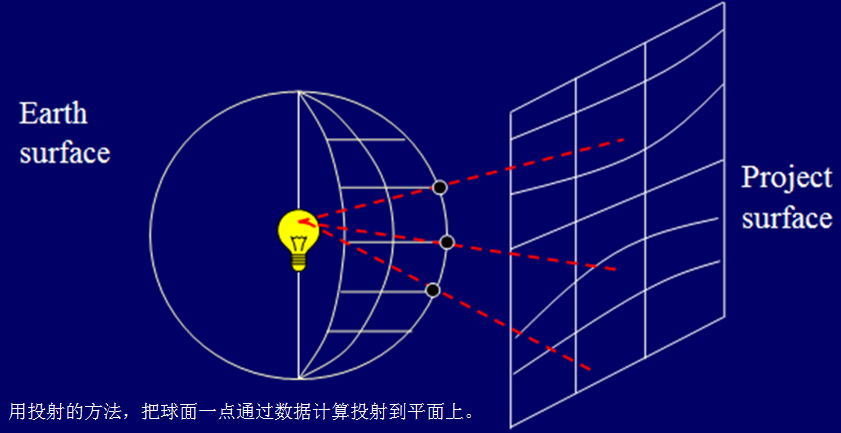
        投影的实质：经纬度坐标 —> 笛卡儿平面直角坐标系

        

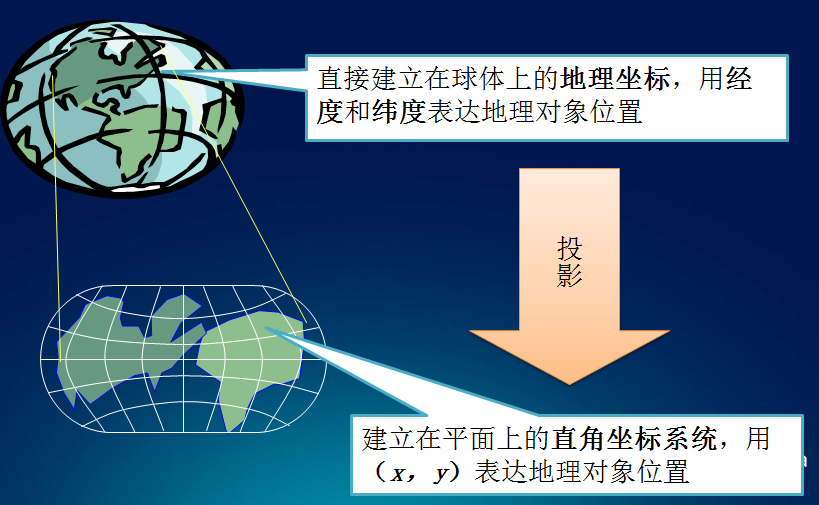
        建立地球椭球面上经纬线网和平面上相应经纬线网的数学基础，也就是建立地球椭球面上的点的地理坐标（λ，φ）与平面上对应点的平面坐标（x，y）之间的函数关系如下图 。当给定不同的具体条件时，将得到不同类型的投影方式。

        

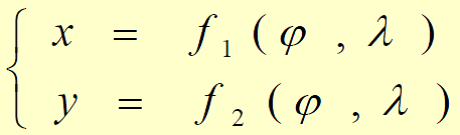
    4.2 投影分类

        地球椭球表面是一种不可能展开的曲面，要把这样一个曲面表现到平面上，就会发生裂隙或褶皱。在投影面上，可运用经纬线的“拉伸”或“压缩”（通过数学手段）来加以避免，以便形成一幅完整的地图。但不可避免会产生变形。

        地图投影的变形通常有：长度变形、面积变形和角度变形。在实际应用中，根据使用地图的目的，限定某种变形。

         按变形性质分类：            

　　　　– 等角投影：角度变形为零（Mercator）            

　　　　– 等积投影：面积变形为零（Albers）            

　　　　– 任意投影：长度、角度和面积都存在变形             其中，各种变形相互联系相互影响：等积与等角互斥，等积投影角度变形大，等角投影面积变形大。          

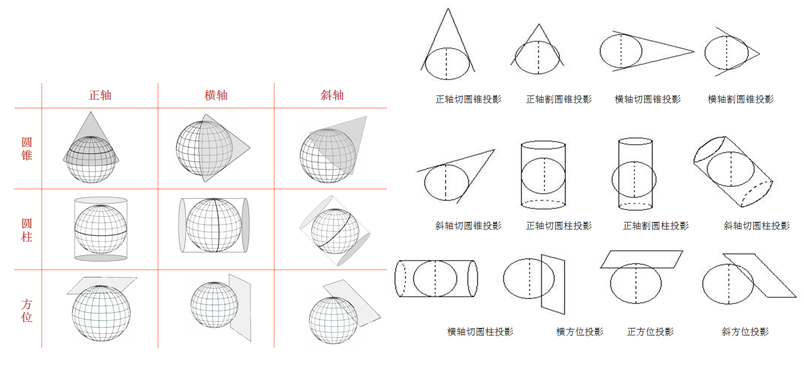
  　　　从投影面类型划分：            

　　　　– 横圆柱投影：投影面为横圆柱            

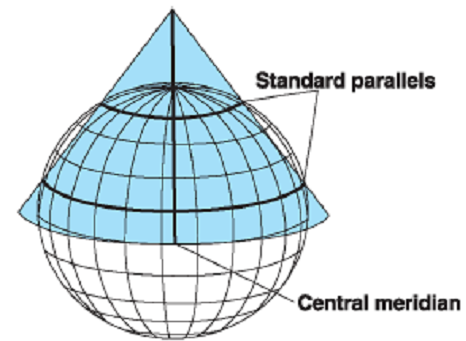
　　　　– 圆锥投影：投影面为圆锥            

　　　　– 方位投影：投影面为平面          

　　　从投影面与地球位置关系划分为：            

　　　　– 正轴投影：投影面中心轴与地轴相互重合            

　　　　– 斜轴投影：投影面中心轴与地轴斜向相交            

　　　　– 横轴投影：投影面中心轴与地轴相互垂直            

　　　　– 相切投影：投影面与椭球体相切            

　　　　– 相割投影：投影面与椭球体相割

        

    4.3 投影选择

        选择地图投影时，主要考虑因素            

　　　　– 制图区域的范围、形状和地理位置（主要因素）            

　　　　– 地图的用途、出版方式及其他特殊要求

        投影选择实例            

　　　　– 世界地图，主要采用正圆柱、伪圆柱和多圆锥投影。在编绘世界航线图、世界交通图与世界时区图时也采用墨卡托投影。            

　　　　– 中国出版的世界地图多采用等差分纬线多圆锥投影 。            

　　　　– 对于半球地图，东、西半球图常选用横轴方位投影；南、北半球图常选用正轴方位投影；水、陆半球图一般选用斜轴方位投影。            

　　　　– 在东西延伸的中纬度地区，一般采用正轴圆锥投影，如中国与美国。            

　　　　– 在南北方向延伸的地区，一般采用横轴圆柱投影或多圆锥投影，如智利与阿根廷 。

        投影参数：          

　　　　标准线            

　　　　　　– 概念：投影面与参考椭球的切线或割线。分为标准纬线与标准经线。            

　　　　　　– 特点：没有变形，也称主比例尺。          

　　　　中心线            

　　　　　　– 概念：是指中央经线（原点经线）与中央纬线（原点纬线），用来定义图投影的中心或者原点。            

　　　　　　– 特点：一般会有变形。

        

          【小结】：            

　　　　– 实现等角、等面积、等距离同时做到的投影不存在。            

　　　　– 投影方式有多种多样，一个国家或地区依据自己所处在的经纬度、幅员大小以及图件用途选择投影方式。            

　　　　– 在大于1：10万的大比例尺图件中，各种投影带来的变形可以忽略。

    4.4 我国常用地图投影（见下篇）

 

——下篇介绍“投影坐标系”

 

原文链接：http://blog.csdn.net/arcgis_all/article/details/8835721