POJ 1463 Strategic game【树形DP】

Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

For example for the tree:

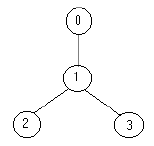
the solution is one soldier ( at the node 1).

Input

The input contains several data sets in text format. Each data set represents a tree with the following description:

• the number of nodes
• the description of each node in the following format
  node_identifier:(number_of_roads) node_identifier₁ node_identifier₂ ... node_identifier_{number_of_roads}
  or
  node_identifier:(0)
• 
  The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.

Output

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following:

Sample Input

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

Sample Output

1
2

code：

// dp[i][0]  在 i 节点不放士兵
// dp[i][1]  在 i 节点放士兵
// dp[i][0]+=dp[j][1]
// dp[i][1]+=min(dp[j][0],dp[j][1])
#include<stdio.h>
#include<string.h>
#define min(a,b)(a)<(b)?(a):(b)
int v[1550];
struct node
{
    int to;
    int next;
}q[15001];
int head[1501],dp[1501][2],tot;
void add(int s,int u)
{
    q[tot].to=u;
    q[tot].next=head[s];
    head[s]=tot++;
}
int dfs(int i)
{
    int j,k;
    dp[i][0]=0;
    dp[i][1]=1;
    for(j=head[i];j;j=q[j].next)
    {
        k=q[j].to;
        if(!v[k])
            dfs(k);
        v[k]=1;
        dp[i][0]+=dp[k][1];
        dp[i][1]+=min(dp[k][0],dp[k][1]);
    }
    return min(dp[i][0],dp[i][1]);
}
int main()
{
    int i,m,n,s,w,root;
    while(scanf("%d",&n)!=EOF)
    {
        tot=1;
        root=-1;
        memset(head,0,sizeof(head));
        memset(v,0,sizeof(v));
        for(i=0;i<n;i++)
        {
            scanf("%d:(%d)",&s,&m);
            if(root==-1) root=s;
            while(m--)
            {
                scanf("%d",&w);
                add(s,w);
            }
        }
        printf("%d\n",dfs(root));
    }
    return 0;
}