Atocder ARC082 F-Sandglass 【思维题】*
Atocder ARC082 F-Sandglass
Problem Statement
We have a sandglass consisting of two bulbs, bulb A and bulb B. These bulbs contain some amount of sand. When we put the sandglass, either bulb A or B lies on top of the other and becomes the upper bulb. The other bulb becomes the lower bulb.
The sand drops from the upper bulb to the lower bulb at a rate of 1 gram per second. When the upper bulb no longer contains any sand, nothing happens.
Initially at time 0, bulb A is the upper bulb and contains a grams of sand; bulb B contains X−a grams of sand (for a total of X grams).
We will turn over the sandglass at time r1,r2,..,rK. Assume that this is an instantaneous action and takes no time. Here, time t refer to the time t seconds after time 0.
You are given Q queries. Each query is in the form of (ti,ai). For each query, assume that a=ai and find the amount of sand that would be contained in bulb A at time ti.
Constraints

All input values are integers.
Input
The input is given from Standard Input in the following format:
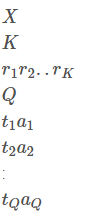
Output
For each query, print the answer in its own line.
Sample Input 1
180
3
60 120 180
3
30 90
61 1
180 180
Sample Output 1
60
1
120
In the first query, 30 out of the initial 90 grams of sand will drop from bulb A, resulting in 60 grams. In the second query, the initial 1 gram of sand will drop from bulb A, and nothing will happen for the next 59 seconds. Then, we will turn over the sandglass, and 1 second after this, bulb A contains 1 gram of sand at the time in question.
Sample Input 2
100
1
100000
4
0 100
90 100
100 100
101 100
Sample Output 2
100
10
0
0
In every query, the upper bulb initially contains 100 grams, and the question in time comes before we turn over the sandglass.
Sample Input 3
100
5
48 141 231 314 425
7
0 19
50 98
143 30
231 55
342 0
365 100
600 10
Sample Output 3
19
52
91
10
58
42
100
题目大意:有一个沙漏分成AB两面,里面共有X个点位的沙子,每一单位时间向下漏1个单位的沙子。
然后有n次操作,每次把沙漏翻转(不消耗时间)
询问当初始A有ai的沙子,B有X-ai的沙子,在t时刻A中有多少沙子
考场上平方暴力
然后想想正解,挺神奇的一道题
首先我们可以用ai=0和X各按照规则跑一遍,跑出每个操作的A中沙子的上下界限
然后我们考虑预处理偏量,不考虑规则,预处理每个时刻的偏量
然后我们对于起始的量ai,直接加上偏量,如果在0和X处理出的区间内就合法,否则变成最靠近的一个
考虑如果直接处理偏量和0或X的折线相交会发生什么
首先明确ai只有可能在0或X触及界限的时候才会相交
那么在相交点右侧一定会存在一个转折点,那么在这个转折点位置ai一定比0低或比X高,所以在这之后ai一定不可能再回到0和X之间
然后就很简单了,是可以做到线性,但我懒,就多挂了一个log
#include<bits/stdc++.h>
using namespace std;
#define N 100010
#define LL long long
int n,q;
LL X,r[N];
struct Node{LL a,t;}p[N];
LL l_line[N],r_line[N];
LL cnt[N];
int main(){
scanf("%lld%d",&X,&n);
r[0]=0;for(int i=1;i<=n;i++)scanf("%lld",&r[i]);
scanf("%d",&q);
for(int i=1;i<=q;i++)scanf("%lld%lld",&p[i].t,&p[i].a);
LL na=0,nb=X;
l_line[0]=0;r_line[0]=X;
for(int tmp=1;tmp<=n;tmp++){
if(tmp&1){
LL tip=min(na,r[tmp]-r[tmp-1]);
na-=tip;
nb+=tip;
}else{
LL tip=min(nb,r[tmp]-r[tmp-1]);
na+=tip;
nb-=tip;
}
l_line[tmp]=na;
}
na=X,nb=0;
for(int tmp=1;tmp<=n;tmp++){
if(tmp&1){
LL tip=min(na,r[tmp]-r[tmp-1]);
na-=tip;
nb+=tip;
}else{
LL tip=min(nb,r[tmp]-r[tmp-1]);
na+=tip;
nb-=tip;
}
r_line[tmp]=na;
}
for(int i=1;i<=n;i++)
if(i&1)cnt[i]=cnt[i-1]-(r[i]-r[i-1]);
else cnt[i]=cnt[i-1]+(r[i]-r[i-1]);
for(int i=1;i<=q;i++){
int ll=1,rr=n,res=0;
while(ll<=rr){
int mid=(ll+rr)>>1;
if(r[mid]<=p[i].t)res=mid,ll=mid+1;
else rr=mid-1;
}
LL pic=p[i].a+cnt[res];
if(l_line[res]>pic)pic=l_line[res];
if(r_line[res]<pic)pic=r_line[res];
if(res&1)pic+=min(X-pic,p[i].t-r[res]);
else pic-=min(pic,p[i].t-r[res]);
printf("%lld\n",pic);
}
return 0;
}

