动态规划(1)——算法导论(16)

我们先从两个问题入手，来学习动态规划。

1. 钢条切割问题

1.1 提出问题

某公司想要把一段长度为n的钢条切割成若干段后卖出，目前市场上长度为i（0<i<10，i为整数）的钢条的价格行情如下：

长度i	1	2	3	4	5	6	7	8	9	10	其他
价格pi	1	5	8	9	10	17	17	20	24	30	0

不考虑切割的成本（即切割成多少段随意），请你给出一个使收益最大化的切割方案。

1.2 分析问题

长度为n的钢条共有\(2^{n-1}\)种切割方案，最简单做法是采用暴力方法，比较所有方案的收益，找出最大值。

暴力破解方法的关键是如何对所有的可能情况进行不重不漏的分类。作如下考虑：

因为无论我们怎么切割，总可以看成是一段完整的长度为i的钢条加上另一部分总长度为n-i的钢条（可能被切割，也可能没有）。
那么切割长度为n的钢条的最大收益可以用如下公式表出：

\[r_n = \max_{1\leq i\leq n}( p_i + r_{n-1}) \]

因此，我们可以采用一种被叫做自顶向下的递归方法去解决该问题。

1.3 自顶向下递归实现

public static int cutRod(int[] p, int n) {
	if (n == 0) {
		return 0;
	}
	int max = Integer.MIN_VALUE;
	for (int i = 1; i <= n && i <= p.length; i++) {
		max = Integer.max(max, p[i - 1] + cutRod(p, n - i));
	}
	return max;
}

在测试时，我们发现，当钢条的长度稍微变大（比如n=30）时，上述程序的运行时间会大大增大。仔细考虑原因，会发现实际上我们做了很多重复的递归操作。比如在求解cutRod(p, n)过程中，我们会递归求解cutRod(p, 0 ~ n-1)，而在求解cutRod(p, n-1)的过程中，同样我们会递归求解cutRod(p, 1 ~ n-1)，可以看出，仅仅就是这两次的调用，就重复调用了n-2次。时间效率当然会下降。

用一个树状图很容易就能看出（以n=4为例）：

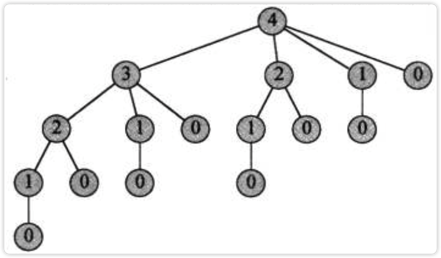
设对于长度为n的钢条，上述程序的运行时间为T(n)，则T(n)可用如下递归式表示：

\[T(n) = 1+ \sum_{i=0}^{n-1}T(j) \]

用数学归纳法很容易计算出\(T(n) = 2^n\)。这也就解释了为什么随着n的“简单”增大，时间会猛增。

1.3 自顶向下递归的改进实现

既然上述程序重复计算了很多次，那么我们可以将每次计算的结果保存起来，下次再需要计算同样的问题时，就直接取出我们计算的结果。

下面是改进之后的代码：

public static int memoziedCutRod(int[] p, int n) {
	memoziedArray = memoziedArray == null ? new int[n] : memoziedArray;
	if (n == 0) {
		return 0;
	}
	if (memoziedArray[n - 1] > 0) {
		return memoziedArray[n - 1];
	}
	int max = Integer.MIN_VALUE;
	for (int i = 1; i <= n && i <= p.length; i++) {
		max = Integer.max(max, p[i - 1] + memoziedCutRod(p, n - i));
	}
	memoziedArray[n - 1] = max;
	return max;
}

再次测试发现，时间效率有明显的提高。

如果上述代码再加上一个记录各长度最优分割方案的“完整段”的长度的“备忘录”，我们便可以很容易的找出长度为1~n的所有情况的详细的最优切割方案。

以下是n=10时的情况：

i	0	1	2	3	4	5	6	7	8	9	10
r[i]	0	1	5	8	10	13	17	18	22	25	30
s[i]	0	1	2	3	2	2	6	1	2	3	10

1.4 自底向上的实现

上述的自顶向下的调用过程在解决问题时，是从最大规模的问题入手，而最大规模的问题是依赖比它小的子问题的，因此便递归的去解决子问题，直到所有的子问题都解决了，该问题也就解决了。

既然我们已经知道了，每个问题的求解必将依赖它的子问题的解，那么我们何不直接按问题规模的从小到大的顺序去依次解决呢？

public static int bottomUpCutRod(int[] p, int n) {
	int[] memoziedArray = new int[n + 1];
	memoziedArray[0] = 0;
	int max = Integer.MIN_VALUE;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= i && j <= p.length; j++) {
			max = Integer.max(max, p[j - 1] + memoziedArray[i - j]);
		}
		memoziedArray[i] = max;
	}
	return max;
}

在上述代码中，我们用了两层嵌套循环替换了递归调用。其中，外层循环来控制问题的规模（规模从i_{n）；内层循环来求解当前规模的问题。因为在每次求解规模为i的问题时，其子问题，即问题规模为1}i-1的问题都已经求解出（存放在）memoziedArray中，因此可以从memoziedArray中直接读取出最优解。

1.5 时间复杂度分析

上面我们已经说过，不带“备忘”的递归调用的时间复杂度为\(2^n\)；带了“备忘”的自底向上的方法的时间复杂度为\(n^2\)，实际上就是一个等差数列的求和；可以想象，自定向下的递归调用实际上和自底向上的方法没有太大的差别（只是求解方向顺序的不同，当然，递归调用由于需要压栈，空间复杂度会较大一些），因此时间复杂度也是\(n^2\)。

下一篇会从矩阵乘法链问题入手，继续探讨动态规划问题。