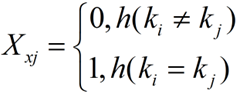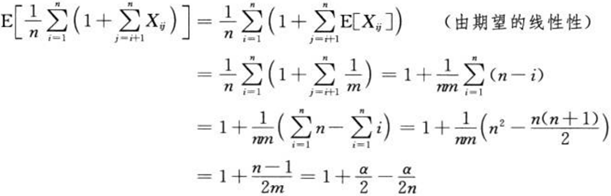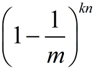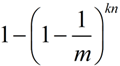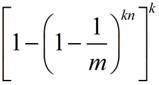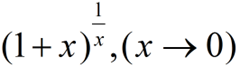散列表(hash table)——算法导论(13)

1. 引言

    许多应用都需要动态集合结构，它至少需要支持Insert，search和delete字典操作。散列表（hash table）是实现字典操作的一种有效的数据结构。

2. 直接寻址表

    在介绍散列表之前，我们先介绍直接寻址表。

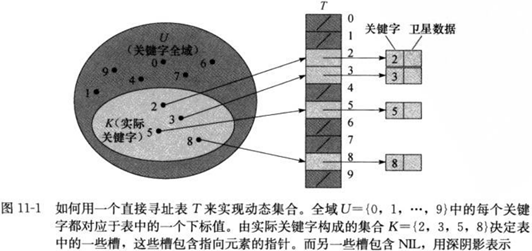
    当关键字的全域U（关键字的范围）比较小时，直接寻址是一种简单而有效的技术。我们假设某应用要用到一个动态集合，其中每个元素的关键字都是取自于全域U=｛0，1，…，m-1｝，其中m不是一个很大的数。另外，假设每个元素的关键字都不同。

   为表示动态集合，我们用一个数组，或称为直接寻址表（direct-address table），记为T[0~m-1]，其中每一个位置（slot，槽）对应全域U中的一个关键字，对应规则是，槽k指向集合中关键字为k的元素，如果集合中没有关键字为k的元素，则T[k]=NIL。

几种字典操作实现起来非常简单：

上述的每一个操作的时间均为O(1)时间。

    在某些应用中，我们其实可以把对象作为元素直接保存在寻址表的槽中，而不需要像上图所示使用指针指向该对象，这样可以节省空间。

3. 散列表

(1) 直接寻址的缺点

    我们可以看出，直接寻址技术有几个明显的缺点：如果全域U很大，那么表T 将要申请一段非常长的空间，很可能会申请失败；对于全域较大，但是元素却十分稀疏的情况，使用这种存储方式将浪费大量的存储空间。

(2) 散列函数

    为了克服直接寻址技术的缺点，而又保持其快速字典操作的优势，我们可以利用散列函数（hash function）

h：U→｛0，1，2，…，m-1｝

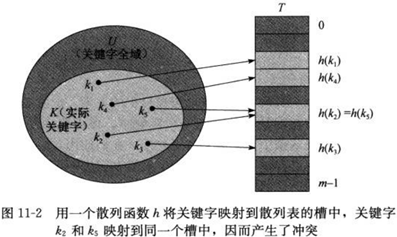
来计算关键字k所在的的位置，简单的讲，散列函数h(k)的作用是将范围较大的关键字映射到一个范围较小的集合中。这时我们可以说，一个具有关键字k的元素被散列到槽h(k)上，或者说h(k)是关键字k的散列值。

示意图如下：

    这时会产生一个问题：两个关键字可能映射到同一槽中（我们称之为冲突（collision）），并且不管你如何优化h(k)函数，这种情况都会发生（因为|U|>m）。

    因此我们现在面临两个问题，一是遇到冲突时如何解决；二是要找出一个的函数h(k)能够尽量的减少冲突；

(3) 通过链表法解决冲突

    我们先来解决第一个问题。

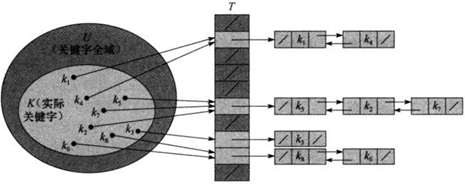
    解决办法就是，我们把同时散列到同一槽中的元素以链表的形式“串联”起来，而该槽中保存的是指向该链表的指针。如下图所示：

    采用该解决办法后，我们可以通过如下的操作方式来进行字典操作：

    下面我们来分析上图各操作的性能。

    首先是插入操作，很明显时间为O(1)。

    然后分析删除操作，其花费的时间相当于从链表中删除一个元素的时间：如果链表T[h(k)]是双链表，花费的时间为O(1)；如果链表T[h(k)]是单链表，则花费的时间和查找操作的渐进运行时间相同。

    下面我们重点分析查找运行时间：

    首先，我们假定任何一个给定元素都等可能地散列在散列表T的任何一个槽位中，且与其他元素被散列在T的哪个位置无关。我们称这个假设为简单均匀散列（simple uniform hashing）。

    不失一般性，我们设散列表T的m个槽位散列了n个元素，则平均每个槽位散列了α = n/m个元素，我们称α为T的装载因子（load factor）。我们记位于槽位j的链表为T[j]（j=1，2，…，m-1），而nj表示链表T[j]的长度，于是有

n = n0+n1+…+nm-1，

且E[nj] = α = n / m。

    现在我们分查找成功和查找不成功两种情况讨论。

    ① 查找不成功

    在查找不成功的情况下，我们需要遍历链表T[j]的每一个元素，而链表T[j]的长度是α，因此需要时间O(α)，加上索引到T(j)的时间O(1)，总时间为θ(1 + α)。

    ② 查找成功

    在查找成功的情况下，我们无法准确知道遍历到链表T[j]的何处停止，因此我们只能讨论平均情况。

    我们设xi是散列表T的第i个元素（假设我们按插入顺序对散列表T中的n个元素进行了1~n的编号），ki表示xi.key，其中i = 1，2，…，n，再定义随机变量Xij=I｛h(ki)=h(kj)｝，即：

在简单均匀散列的假设下有

P｛h(ki)=h(kj)｝ = 1 / m，

E[Xij] = 1 / m。

则所需检查的元素的数目的期望是：

因此，一次成功的检查所需要的时间是O(2 + α / 2 –α / 2n) = θ(1 + α)。

    综合上面的分析，在平均下，全部的字典操作都可以在O(1)时间下完成。

4. 散列函数

    现在我们来解决第二个问题：如何构造一个好的散列函数。

    一个好的散列函数应（近似地）满足简单均匀散列：每个关键字都等可能的被散列到各个槽位，并与其他关键字散列到哪一个槽位无关（但很遗憾，我们一般无法检验这一条件是否成立）。

    在实际应用中，常常可以可以运用启发式方法来构造性能好的散列函数。设计过程中，可以利用关键字分布的有用信息。一个好的方法导出的散列值，在某种程度上应独立于数据可能存在的任何模式。

    下面给出两种基本的构造散列函数的方法：

(1) 除法散列法

    除法散列法的做法很简单，就是让关键字k去除以一个数m，取余数，这样就将k映射到m个槽位中的某一个，即散列函数是：

h(k) = k mod m ，

    由于只做一次除法运算，该方法的速度是非常快的。但应当注意的是，我们在选取m的值时，应当避免一些选取一些值。例如，m不应是2的整数幂，因为如果m = 2 ^ p，则h(k)就是k的p个最低位数字。除非我们已经知道各种最低p位的排列是等可能的，否则我们最好慎重的选择m。而一个不太接近2的整数幂的素数，往往是较好的选择。

(2) 乘法散列法

    该方法包含两个步骤。第一步：用关键字k乘以A（0 < A < 1），并提取kA的小数部分；第二步：用m乘以这个值，在向下取整，即散列函数是：

h(k) = [m (kA mod 1)]，

这里“kA mod 1”的是取kA小数部分的意思，即kA –[kA]。

    乘法散列法的一个优点是，一般我们对m的选择不是特别的关键，一般选择它为2的整数幂即可。虽然这个方法对任意的A都适用，但Knuth认为，A ≈ （√5 - 1）/ 2 = 0.618033988…是一个比较理想的值

(5) 布隆过滤器

    布隆过滤器（Bloom Filter）是一种常被用来检验一个元素是否在一个集合里面的算法（从这里我们可以看出，这个集合只需要保存比对元素的“指纹”即可，而不需要保存比对元素的全部信息），由一个很长的二进制向量和一系列随机映射函数组成。相较于其他算法，它具有空间利用率高，检测速度快等优点。

    在介绍布隆过滤器之前，我们先假设这样一种场景：某公司致力于解决用户常常遭遇骚扰电话的问题。该公司打算建立一个骚扰电话号码的黑名单，即把所有骚扰电话的号码保存到一张hash表中。当用户接到某个陌生电话时，服务器会立即将该号码与黑名单进行比对，若比对成功，则对该号码进行拦截。

    他们当然不会直接将骚扰电话号码保存在hash表中，而是对每一个号码利用某种算法进行数据压缩，最终得到一个8字节的信息指纹，然后将其存入表中。但即便如此，问题还是来了：由于hash表的空间利用率大约只有50%，等价换算过来，储存一个号码将要花费16字节的空间。按照这样计算，储存1亿个号码将要花费大约1.6G的空间，储存几十亿的号码可能需要上百G的空间。那么有没有更好解决办法呢？

    这时，布隆过滤器就派上用场了。假设我们有1亿条骚扰电话号码需要记录，我们的做法是，首先建立一个2亿字节（即16亿位，并假设我们对这16亿位以1~16亿的顺序进行了编号）的向量，将每位都置为0。当要插入某个电话号码x时，我们使用某种算法（该算法可以做到每个位被映射的概率是一样的，且某个映射的分布与其他的映射分布无关）让号码x映射到1~16亿中的8个位上，然后把这8个位设为1。当查找时，利用同样的方法将号码映射到8个位上，若这8个位都为1，则说明该号码在黑名单中，否则就不在。

    我们可以发现，布隆过滤器的做法在思想上和hash函数将关键字映射到hash表的做法很相似，因此布隆过滤器也会遇到冲突问题，这会导致将一个“好”的号码误判为骚扰号码（但绝对不会将骚扰号码误判为一个“好”的号码）。下面我们通过计算来证明，在大多数情况和场景中，这种误判我们是可以忍受的。

    假设某布隆过滤器共有的m个槽位，我们要把n个号码添加到其中，而每个号码会映射k个槽位。那么，添加这n个号码将会产生kn次映射。因为这m个槽位中，每个槽被映射到的概率是相等的。因此，

在一次映射中，某个槽位被映射到的概率（即该槽位值为1的概率）为

该槽位值为0的概率为

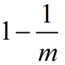
经过kn次映射后，某个槽值为0的概率为

为1的概率为

所以，误判（k个槽位均为1）的概率就为

利用 ，上式可化为：

这时我们注意到，当k=1时，情况就就变成了hash table的情况，

根据自变量的不同我们分以下两种方式讨论：

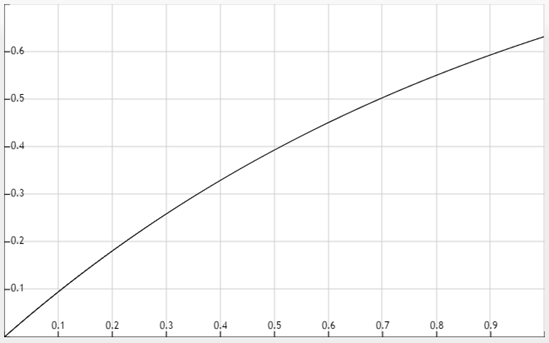
① 我们把误判率p看作关于装载因子α的函数（k看作常数），这时我们从函数 的函数图像

 

中可以得出一下结论：

    随着装载因子α（α = n / m）的增大，误判率（或者是产生冲突的概率）也将增大，但增长速度逐渐减慢。

    要使误判率小于0.5，装载因子必须小于0.7。这也从某种程度上解释了为什么JDK HashMap的装载因子默认是0.75。

② 我们把误判率p看作关于k的函数（α作为常数），通过对p求导分析，我们发现，当k=ln2 / α时，误判率p取得最小值。此时，p = 2^(-k)（或者k = – ln p / ln 2），这个结论让我们能够根据可以忍受的误判率计算出最为合适的k值。

下面给出一个BloomFilter的Java实现代码（来自：https://github.com/MagnusS/Java-BloomFilter，只是把其中的变量和方法名换成了上文提及的）：

public class BloomFilter<E> implements Serializable {
    private static final long serialVersionUID = -9077350041930475408L;

    private BitSet bitset;// 二进制向量
    private int slotSize; // 二进制向量的总位（槽）数（文中的m）
    private double loadFactor; // 装载因子 （文中的α）
    private int capacity; // 布隆过滤器的容量（文中的n）
    private int size; // 装载的数目
    private int k; // 一个元素对应的位数（文中的k）

    static final Charset charset = Charset.forName("UTF-8");
    static final String hashName = "MD5";// 默认采用MD5算法，也可改为SHA1
    static final MessageDigest digestFunction;

    static {
        MessageDigest tmp;
        try {
            tmp = java.security.MessageDigest.getInstance(hashName);
        } catch (NoSuchAlgorithmException e) {
            tmp = null;
        }
        digestFunction = tmp;
    }

    public BloomFilter(int slotSize, int capacity) {
        this(slotSize / (double) capacity, capacity, (int) Math.round((slotSize / (double) capacity) * Math.log(2.0)));
    }

    public BloomFilter(double falsePositiveProbability, int capacity) {
        this(Math.log(2) / (Math.ceil(-(Math.log(falsePositiveProbability) / Math.log(2)))),//loadFactor = ln2 / k;
                capacity, //
                (int) Math.ceil(-(Math.log(falsePositiveProbability) / Math.log(2)))); //k = -ln p / ln2
    }

    public BloomFilter(int slotSize, int capacity, int size, BitSet filterData) {
        this(slotSize, capacity);
        this.bitset = filterData;
        this.size = size;
    }

    public BloomFilter(double loadFactor, int capacity, int k) {
        size = 0;
        this.loadFactor = loadFactor;
        this.capacity = capacity;
        this.k = k;
        this.slotSize = (int) Math.ceil(capacity * loadFactor);
        this.bitset = new BitSet(slotSize);
    }

    public static int createHash(String val, Charset charset) {
        return createHash(val.getBytes(charset));
    }

    public static int createHash(String val) {
        return createHash(val, charset);
    }

    public static int createHash(byte[] data) {
        return createHashes(data, 1)[0];
    }

    public static int[] createHashes(byte[] data, int hashes) {
        int[] result = new int[hashes];

        int k = 0;
        byte salt = 0;
        while (k < hashes) {
            byte[] digest;
            synchronized (digestFunction) {
                digestFunction.update(salt);
                salt++;
                digest = digestFunction.digest(data);
            }

            for (int i = 0; i < digest.length / 4 && k < hashes; i++) {
                int h = 0;
                for (int j = (i * 4); j < (i * 4) + 4; j++) {
                    h <<= 8;
                    h |= ((int) digest[j]) & 0xFF;
                }
                result[k] = h;
                k++;
            }
        }
        return result;
    }

    /**
     * Compares the contents of two instances to see if they are equal.
     *
     * @param obj
     *            is the object to compare to.
     * @return True if the contents of the objects are equal.
     */
    @Override
    public boolean equals(Object obj) {
        if (obj == null) {
            return false;
        }
        if (getClass() != obj.getClass()) {
            return false;
        }
        final BloomFilter<E> other = (BloomFilter<E>) obj;
        if (this.capacity != other.capacity) {
            return false;
        }
        if (this.k != other.k) {
            return false;
        }
        if (this.slotSize != other.slotSize) {
            return false;
        }
        if (this.bitset != other.bitset && (this.bitset == null || !this.bitset.equals(other.bitset))) {
            return false;
        }
        return true;
    }

    /**
     * Calculates a hash code for this class.
     * 
     * @return hash code representing the contents of an instance of this class.
     */
    @Override
    public int hashCode() {
        int hash = 7;
        hash = 61 * hash + (this.bitset != null ? this.bitset.hashCode() : 0);
        hash = 61 * hash + this.capacity;
        hash = 61 * hash + this.slotSize;
        hash = 61 * hash + this.k;
        return hash;
    }

    /**
     * Calculates the expected probability of false positives based on the
     * number of expected filter elements and the size of the Bloom filter.
     * <br />
     * <br />
     * The value returned by this method is the <i>expected</i> rate of false
     * positives, assuming the number of inserted elements equals the number of
     * expected elements. If the number of elements in the Bloom filter is less
     * than the expected value, the true probability of false positives will be
     * lower.
     *
     * @return expected probability of false positives.
     */
    public double expectedFalsePositiveProbability() {
        return getFalsePositiveProbability(capacity);
    }

    /**
     * Calculate the probability of a false positive given the specified number
     * of inserted elements.
     *
     * @param numberOfElements
     *            number of inserted elements.
     * @return probability of a false positive.
     */
    public double getFalsePositiveProbability(double numberOfElements) {
        // (1 - e^(-k * n / m)) ^ k
        return Math.pow((1 - Math.exp(-k * (double) numberOfElements / (double) slotSize)), k);

    }

    /**
     * Get the current probability of a false positive. The probability is
     * calculated from the size of the Bloom filter and the current number of
     * elements added to it.
     *
     * @return probability of false positives.
     */
    public double getFalsePositiveProbability() {
        return getFalsePositiveProbability(size);
    }

    /**
     * Returns the value chosen for K.<br />
     * <br />
     * K is the optimal number of hash functions based on the size of the Bloom
     * filter and the expected number of inserted elements.
     *
     * @return optimal k.
     */
    public int getK() {
        return k;
    }

    /**
     * Sets all bits to false in the Bloom filter.
     */
    public void clear() {
        bitset.clear();
        size = 0;
    }

    /**
     * Adds an object to the Bloom filter. The output from the object's
     * toString() method is used as input to the hash functions.
     *
     * @param element
     *            is an element to register in the Bloom filter.
     */
    public void add(E element) {
        add(element.toString().getBytes(charset));
    }

    /**
     * Adds an array of bytes to the Bloom filter.
     *
     * @param bytes
     *            array of bytes to add to the Bloom filter.
     */
    public void add(byte[] bytes) {
        int[] hashes = createHashes(bytes, k);
        for (int hash : hashes)
            bitset.set(Math.abs(hash % slotSize));
        size++;
    }

    /**
     * Adds all elements from a Collection to the Bloom filter.
     * 
     * @param c
     *            Collection of elements.
     */
    public void addAll(Collection<? extends E> c) {
        for (E element : c)
            add(element);
    }

    /**
     * Returns true if the element could have been inserted into the Bloom
     * filter. Use getFalsePositiveProbability() to calculate the probability of
     * this being correct.
     *
     * @param element
     *            element to check.
     * @return true if the element could have been inserted into the Bloom
     *         filter.
     */
    public boolean contains(E element) {
        return contains(element.toString().getBytes(charset));
    }

    /**
     * Returns true if the array of bytes could have been inserted into the
     * Bloom filter. Use getFalsePositiveProbability() to calculate the
     * probability of this being correct.
     *
     * @param bytes
     *            array of bytes to check.
     * @return true if the array could have been inserted into the Bloom filter.
     */
    public boolean contains(byte[] bytes) {
        int[] hashes = createHashes(bytes, k);
        for (int hash : hashes) {
            if (!bitset.get(Math.abs(hash % slotSize))) {
                return false;
            }
        }
        return true;
    }

    /**
     * Returns true if all the elements of a Collection could have been inserted
     * into the Bloom filter. Use getFalsePositiveProbability() to calculate the
     * probability of this being correct.
     * 
     * @param c
     *            elements to check.
     * @return true if all the elements in c could have been inserted into the
     *         Bloom filter.
     */
    public boolean containsAll(Collection<? extends E> c) {
        for (E element : c)
            if (!contains(element))
                return false;
        return true;
    }

    /**
     * Read a single bit from the Bloom filter.
     * 
     * @param bit
     *            the bit to read.
     * @return true if the bit is set, false if it is not.
     */
    public boolean getBit(int bit) {
        return bitset.get(bit);
    }

    /**
     * Set a single bit in the Bloom filter.
     * 
     * @param bit
     *            is the bit to set.
     * @param value
     *            If true, the bit is set. If false, the bit is cleared.
     */
    public void setBit(int bit, boolean value) {
        bitset.set(bit, value);
    }

    /**
     * Return the bit set used to store the Bloom filter.
     * 
     * @return bit set representing the Bloom filter.
     */
    public BitSet getBitSet() {
        return bitset;
    }

    /**
     * Returns the number of bits in the Bloom filter. Use count() to retrieve
     * the number of inserted elements.
     *
     * @return the size of the bitset used by the Bloom filter.
     */
    public int slotSize() {
        return slotSize;
    }

    /**
     * Returns the number of elements added to the Bloom filter after it was
     * constructed or after clear() was called.
     *
     * @return number of elements added to the Bloom filter.
     */
    public int size() {
        return size;
    }

    /**
     * Returns the expected number of elements to be inserted into the filter.
     * This value is the same value as the one passed to the constructor.
     *
     * @return expected number of elements.
     */
    public int capacity() {
        return capacity;
    }

    /**
     * Get expected number of bits per element when the Bloom filter is full.
     * This value is set by the constructor when the Bloom filter is created.
     * See also getBitsPerElement().
     *
     * @return expected number of bits per element.
     */
    public double getLoadFactor() {
        return this.loadFactor;
    }
}