Deep Learning 19_深度学习UFLDL教程:Convolutional Neural Network_Exercise(斯坦福大学深度学习教程)
理论知识:Optimization: Stochastic Gradient Descent和Convolutional Neural Network
CNN卷积神经网络推导和实现、Deep learning:五十一(CNN的反向求导及练习)
Deep Learning 学习随记(八)CNN(Convolutional neural network)理解
ufldl学习笔记与编程作业:Convolutional Neural Network(卷积神经网络)
【UFLDL】Exercise: Convolutional Neural Network
基础知识
下面是Convolutional Neural Network的翻译
概述
CNN是由一个或多个卷积层(其后常跟一个下采样层)和一个或多个全连接层组成的多层神经网络。CNN的输入是2维图像(或者其他2维输入,如语音信号)。它通过局部连接和权值共享,再通过池化可得到平移不变特征。CNN的另一个优点就是易于训练,相比同样隐含层单元的全连接网络,它需要训练的参数个数要少得多。本文将介绍CNN的结构和后向传播算法,该算法用于计算对模型参数的梯度。卷积和池化可看前面相应的教程。
结构
CNN由一些卷积层和下采样层交替组成,也可视需要在最后加全连接层。一个卷积层的输入是m*m*r的图像,其中m是图像的高度和宽度,r是通道数,如RGB图像的r=3。卷积层有k个滤波器(或核函数),大小为n*n*q,其中n小于图像的维数,q小于等于r且每个滤波器的q可能不一样。滤波器的大小产生局部连接结构,该结构是由每个滤波器与输入图像卷积得到k个特征图,每个特征图大小为m-n+1。然后,每个特征图通过p*p连续区域的平均或最大池化的方式来子采样,其中p一般取2(当输入为小图像时,如MNIST)和5(当输入是大图像时)之间。在子采样层的前后均需对每个特征图加一个附加偏置项和sigmoid非线性变化。下图显示了一个由卷积层和子采样层组成的CNN。其中,相同颜色的单元共享权值。
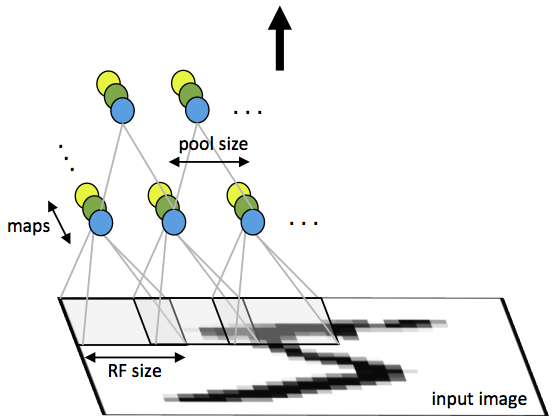
图1.卷积神经网络的带池化的第一层。相同颜色的神经元共享权值,不同颜色神经元表示不同的特征图。
在卷积层的最后可能会有一些全连接层。该层是与一个标准多层神经网络中的层是一样的。
后向传播
δ(l+1)中是l+1层的残差,代价函数为J(W,b;x,y),其中(W,b)是参数,(x,y)分别是训练数据和标签。则l层的残差和梯度分别为:
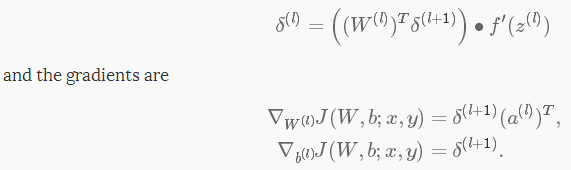
如果l层是一个卷积层和子采样层,则其残差为:

其中,k是滤波器个数, 是激活函数的偏层数。通过计算传入池化层每个神经元的残差,子采样必须通过池化层传播残差。
是激活函数的偏层数。通过计算传入池化层每个神经元的残差,子采样必须通过池化层传播残差。
最后,为了计算特征图的梯度,利用边缘处理卷积运算得到残差矩阵,再翻转残差矩阵。在卷积层翻转滤波器和最后翻转残差矩阵效果是一样的。
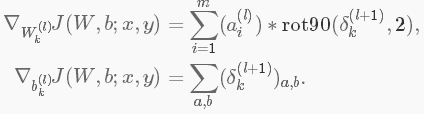
其中,
a(L)是L层的输入,a(1)是输入图像。 是一个合理的卷积运算,该卷积是第l层的第i个输入与对第k个滤波器的残差相卷。
是一个合理的卷积运算,该卷积是第l层的第i个输入与对第k个滤波器的残差相卷。
练习
练习内容:UFLDL:Exercise: Convolutional Neural Network。利用卷积神经网络实现数字分类。该神经网络有2层,第一层是卷积和子采样层,第二层是全连接层。即:本节的网络结构为:一个卷积层+一个pooling层+一个softmax层。本节练习中,输入图像为28*28,卷积核大小为9*9,卷积层特征个数(即:卷积核个数)为20个,池化连续区域为2*2,输出为类别为10类。
参考:【UFLDL】Exercise: Convolutional Neural Network讲解非常详细
注意:本练习中的卷积核,并不是由自编码器学习的特征,而是随机随机始化所得
一些matlab函数
1.addpath
语法:
添加路径:addpath('当前路径中的文件夹名1','当前路径下的文件夹名2','当前路径中的文件夹名n');【即可一次性添加多个路径】
addpath('./上级目录中的文件夹1','./上级目录中的文件夹2','./上级目录中的文件夹n');
addpath('../更上一级目录中的文件夹1','../更上一级目录中的文件夹2','../更上一级目录中的文件夹n');
3.sub2ind函数
ind2sub函数可以用来把矩阵元素的index转换成对应的下标(determines the equivalent subscript values corresponding to a single index into an array)
例如: 一个4*5的矩阵A,第2行第2个元素的index的6(matlab中matrix是按列顺序排列),可以用ind2sub函数来计算这个元素的下标 [I,J] = ind2sub(size(A),6)
4.sparse和full函数
见Deep Learning 6_深度学习UFLDL教程:Softmax Regression_Exercise(斯坦福大学深度学习教程)
下面这句话经常可见:
groundTruth = full(sparse(labels, 1:numImages, 1));
它得到的结果是这样一个矩阵:在第i行第j列元素值为1,其他元素为0,其中,i是向量labels内的第k个元素值,j是向量1:numImages内的第k个元素值。
故,在cnnCost.m中计算cost的代码为:
logProbs = log(probs); labelIndex=sub2ind(size(logProbs), labels', 1:size(logProbs,2)); %找出矩阵logProbs的线性索引,行由labels指定,列由1:size(logProbs,2)指定,生成线性索引返回给labelIndex values = logProbs(labelIndex); cost = -sum(values); weightDecayCost = (weightDecay/2) * (sum(Wd(:) .^ 2) + sum(Wc(:) .^ 2)); cost = cost / numImages+weightDecayCost;
可把它替换为:
groundTruth = full(sparse(labels, 1:numImages, 1)); cost = -1./numImages*groundTruth(:)'*log(probs(:))+(weightDecay/2.)*(sum(Wd(:).^2)+sum(Wc(:).^2)); %加入一个惩罚项
变得效率更快,代码更简洁。
练习步骤
STEP 1:实现CNN代价函数和梯度计算
STEP 1a: Forward Propagation
STEP 1b: Calculate Cost
代价函数:

其中,J(W,b)为:
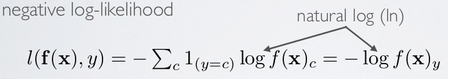
STEP 1c: Backpropagation
softmax 层误差:softmaxError,见Deep learning:五十一(CNN的反向求导及练习)
pool 层误差:poolError,这一层首先根据公式δl = Wδl+1 * f'(zl)(pool层没有f'(zl)这一项)计算该层的error。即poolError为:δl = Wδl+1
展开poolError为unpoolError,
convolution层误差:convError,还是根据公式δl = Wδl+1 * f'(zl)来计算
STEP 1d: Gradient Calculation
Wd和bd的梯度计算公式:
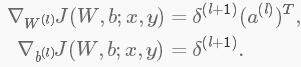
Step 2: Gradient Check
非常重要的一步
Step 3: Learn Parameters
在minFuncSGD中加上冲量的影响即可。
Step 4: Test
结果为:

代码
cnnTrain.m
%% Convolution Neural Network Exercise % Instructions % ------------ % % This file contains code that helps you get started in building a single. % layer convolutional nerual network. In this exercise, you will only % need to modify cnnCost.m and cnnminFuncSGD.m. You will not need to % modify this file. %%====================================================================== %% STEP 0: Initialize Parameters and Load Data % Here we initialize some parameters used for the exercise. % Configuration imageDim = 28; numClasses = 10; % Number of classes (MNIST images fall into 10 classes) filterDim = 9; % Filter size for conv layer,9*9 numFilters = 20; % Number of filters for conv layer poolDim = 2; % Pooling dimension, (should divide imageDim-filterDim+1) % Load MNIST Train addpath ../common/; images = loadMNISTImages('../common/train-images-idx3-ubyte'); images = reshape(images,imageDim,imageDim,[]); labels = loadMNISTLabels('../common/train-labels-idx1-ubyte'); labels(labels==0) = 10; % Remap 0 to 10 % Initialize Parameters,theta=(2165,1),2165=9*9*20+20+100*20*10+10 theta = cnnInitParams(imageDim,filterDim,numFilters,poolDim,numClasses); %%====================================================================== %% STEP 1: Implement convNet Objective % Implement the function cnnCost.m. %%====================================================================== %% STEP 2: Gradient Check % Use the file computeNumericalGradient.m to check the gradient % calculation for your cnnCost.m function. You may need to add the % appropriate path or copy the file to this directory. % DEBUG=false; % set this to true to check gradient DEBUG = true; if DEBUG % To speed up gradient checking, we will use a reduced network and % a debugging data set db_numFilters = 2; db_filterDim = 9; db_poolDim = 5; db_images = images(:,:,1:10); db_labels = labels(1:10); db_theta = cnnInitParams(imageDim,db_filterDim,db_numFilters,... db_poolDim,numClasses); [cost grad] = cnnCost(db_theta,db_images,db_labels,numClasses,... db_filterDim,db_numFilters,db_poolDim); % Check gradients numGrad = computeNumericalGradient( @(x) cnnCost(x,db_images,... db_labels,numClasses,db_filterDim,... db_numFilters,db_poolDim), db_theta); % Use this to visually compare the gradients side by side disp([numGrad grad]); diff = norm(numGrad-grad)/norm(numGrad+grad); % Should be small. In our implementation, these values are usually % less than 1e-9. disp(diff); assert(diff < 1e-9,... 'Difference too large. Check your gradient computation again'); end; %%====================================================================== %% STEP 3: Learn Parameters % Implement minFuncSGD.m, then train the model. % 因为是采用的mini-batch梯度下降法,所以总共对样本的循环次数次数比标准梯度下降法要少 % 很多,因为每次循环中权值已经迭代多次了 options.epochs = 3; options.minibatch = 256; options.alpha = 1e-1; options.momentum = .95; opttheta = minFuncSGD(@(x,y,z) cnnCost(x,y,z,numClasses,filterDim,... numFilters,poolDim),theta,images,labels,options); save('theta.mat','opttheta'); %%====================================================================== %% STEP 4: Test % Test the performance of the trained model using the MNIST test set. Your % accuracy should be above 97% after 3 epochs of training testImages = loadMNISTImages('../common/t10k-images-idx3-ubyte'); testImages = reshape(testImages,imageDim,imageDim,[]); testLabels = loadMNISTLabels('../common/t10k-labels-idx1-ubyte'); testLabels(testLabels==0) = 10; % Remap 0 to 10 [~,cost,preds]=cnnCost(opttheta,testImages,testLabels,numClasses,... filterDim,numFilters,poolDim,true); acc = sum(preds==testLabels)/length(preds); % Accuracy should be around 97.4% after 3 epochs fprintf('Accuracy is %f\n',acc);
cnnCost.m
function [cost, grad, preds] = cnnCost(theta,images,labels,numClasses,... filterDim,numFilters,poolDim,pred) % Calcualte cost and gradient for a single layer convolutional % neural network followed by a softmax layer with cross entropy % objective. % % Parameters: % theta - unrolled parameter vector % images - stores images in imageDim x imageDim x numImges % array % numClasses - number of classes to predict % filterDim - dimension of convolutional filter % numFilters - number of convolutional filters % poolDim - dimension of pooling area % pred - boolean only forward propagate and return % predictions % % % Returns: % cost - cross entropy cost % grad - gradient with respect to theta (if pred==False) % preds - list of predictions for each example (if pred==True) if ~exist('pred','var') pred = false; end; weightDecay = 0.0001; imageDim = size(images,1); % height/width of image numImages = size(images,3); % number of images %% Reshape parameters and setup gradient matrices % Wc is filterDim x filterDim x numFilters parameter matrix %convolution参数 % bc is the corresponding bias % Wd is numClasses x hiddenSize parameter matrix where hiddenSize % is the number of output units from the convolutional layer %这个convolutional layer应该是包含了卷积层和pool层 % bd is corresponding bias [Wc, Wd, bc, bd] = cnnParamsToStack(theta,imageDim,filterDim,numFilters,... poolDim,numClasses); % Same sizes as Wc,Wd,bc,bd. Used to hold gradient w.r.t above params. Wc_grad = zeros(size(Wc)); Wd_grad = zeros(size(Wd)); bc_grad = zeros(size(bc)); bd_grad = zeros(size(bd)); %%====================================================================== %% STEP 1a: Forward Propagation % In this step you will forward propagate the input through the % convolutional and subsampling (mean pooling) layers. You will then use % the responses from the convolution and pooling layer as the input to a % standard softmax layer. %% Convolutional Layer % For each image and each filter, convolve the image with the filter, add % the bias and apply the sigmoid nonlinearity. Then subsample the % convolved activations with mean pooling. Store the results of the % convolution in activations and the results of the pooling in % activationsPooled. You will need to save the convolved activations for % backpropagation. convDim = imageDim-filterDim+1; % dimension of convolved output outputDim = (convDim)/poolDim; % dimension of subsampled output % convDim x convDim x numFilters x numImages tensor for storing activations activations = zeros(convDim,convDim,numFilters,numImages); % outputDim x outputDim x numFilters x numImages tensor for storing % subsampled activations activationsPooled = zeros(outputDim,outputDim,numFilters,numImages); %%% YOUR CODE HERE %%% %调用之前写的两个函数 activations = cnnConvolve(filterDim, numFilters, images, Wc, bc); activationsPooled = cnnPool(poolDim, activations); % Reshape activations into 2-d matrix, hiddenSize x numImages, % for Softmax layer activationsPooled = reshape(activationsPooled,[],numImages);%就变成了传统的softmax模式 %% Softmax Layer % Forward propagate the pooled activations calculated above into a % standard softmax layer. For your convenience we have reshaped % activationPooled into a hiddenSize x numImages matrix. Store the % results in probs. % numClasses x numImages for storing probability that each image belongs to % each class. probs = zeros(numClasses,numImages); %%% YOUR CODE HERE %%% z = Wd*activationsPooled; z = bsxfun(@plus,z,bd); %z = Wd * activationsPooled+repmat(bd,[1,numImages]); z = bsxfun(@minus,z,max(z,[],1));%减去最大值,减少一个维度,防止溢出 z = exp(z); probs = bsxfun(@rdivide,z,sum(z,1)); preds = probs; %%====================================================================== %% STEP 1b: Calculate Cost % In this step you will use the labels given as input and the probs % calculate above to evaluate the cross entropy objective. Store your % results in cost. cost = 0; % save objective into cost %%% YOUR CODE HERE %%% logProbs = log(probs); labelIndex=sub2ind(size(logProbs), labels', 1:size(logProbs,2)); %找出矩阵logProbs的线性索引,行由labels指定,列由1:size(logProbs,2)指定,生成线性索引返回给labelIndex values = logProbs(labelIndex); cost = -sum(values); weightDecayCost = (weightDecay/2) * (sum(Wd(:) .^ 2) + sum(Wc(:) .^ 2)); cost = cost / numImages+weightDecayCost; %Make sure to scale your gradients by the inverse size of the training set %if you included this scale in the cost calculation otherwise your code will not pass the numerical gradient check. % Makes predictions given probs and returns without backproagating errors. if pred [~,preds] = max(probs,[],1); preds = preds'; grad = 0; return; end; %%====================================================================== %% STEP 1c: Backpropagation % Backpropagate errors through the softmax and convolutional/subsampling % layers. Store the errors for the next step to calculate the gradient. % Backpropagating the error w.r.t the softmax layer is as usual. To % backpropagate through the pooling layer, you will need to upsample the % error with respect to the pooling layer for each filter and each image. % Use the kron function and a matrix of ones to do this upsampling % quickly. %%% YOUR CODE HERE %%% %softmax残差 targetMatrix = zeros(size(probs)); targetMatrix(labelIndex) = 1; softmaxError = probs-targetMatrix; %pool层残差 poolError = Wd'*softmaxError; poolError = reshape(poolError, outputDim, outputDim, numFilters, numImages); unpoolError = zeros(convDim, convDim, numFilters, numImages); unpoolingFilter = ones(poolDim); poolArea = poolDim*poolDim; %展开poolError为unpoolError for imageNum = 1:numImages for filterNum = 1:numFilters e = poolError(:, :, filterNum, imageNum); unpoolError(:, :, filterNum, imageNum) = kron(e, unpoolingFilter)./poolArea; end end convError = unpoolError .* activations .* (1 - activations); %%====================================================================== %% STEP 1d: Gradient Calculation % After backpropagating the errors above, we can use them to calculate the % gradient with respect to all the parameters. The gradient w.r.t the % softmax layer is calculated as usual. To calculate the gradient w.r.t. % a filter in the convolutional layer, convolve the backpropagated error % for that filter with each image and aggregate over images. %%% YOUR CODE HERE %%% %softmax梯度 Wd_grad = (1/numImages).*softmaxError * activationsPooled'+weightDecay * Wd; % l+1层残差 * l层激活值 bd_grad = (1/numImages).*sum(softmaxError, 2); % Gradient of the convolutional layer bc_grad = zeros(size(bc)); Wc_grad = zeros(size(Wc)); %计算bc_grad for filterNum = 1 : numFilters e = convError(:, :, filterNum, :); bc_grad(filterNum) = (1/numImages).*sum(e(:)); end %翻转convError for filterNum = 1 : numFilters for imageNum = 1 : numImages e = convError(:, :, filterNum, imageNum); convError(:, :, filterNum, imageNum) = rot90(e, 2); end end for filterNum = 1 : numFilters Wc_gradFilter = zeros(size(Wc_grad, 1), size(Wc_grad, 2)); for imageNum = 1 : numImages Wc_gradFilter = Wc_gradFilter + conv2(images(:, :, imageNum), convError(:, :, filterNum, imageNum), 'valid'); end Wc_grad(:, :, filterNum) = (1/numImages).*Wc_gradFilter; end Wc_grad = Wc_grad + weightDecay * Wc; %% Unroll gradient into grad vector for minFunc grad = [Wc_grad(:) ; Wd_grad(:) ; bc_grad(:) ; bd_grad(:)]; end
cnnConvolve.m
function convolvedFeatures = cnnConvolve(filterDim, numFilters, images, W, b) %cnnConvolve Returns the convolution of the features given by W and b with %the given images % % Parameters: % filterDim - filter (feature) dimension % numFilters - number of feature maps % images - large images to convolve with, matrix in the form % images(r, c, image number) % W, b - W, b for features from the sparse autoencoder % W is of shape (filterDim,filterDim,numFilters) % b is of shape (numFilters,1) % % Returns: % convolvedFeatures - matrix of convolved features in the form % convolvedFeatures(imageRow, imageCol, featureNum, imageNum) numImages = size(images, 3); imageDim = size(images, 1); convDim = imageDim - filterDim + 1; convolvedFeatures = zeros(convDim, convDim, numFilters, numImages); % Instructions: % Convolve every filter with every image here to produce the % (imageDim - filterDim + 1) x (imageDim - filterDim + 1) x numFeatures x numImages % matrix convolvedFeatures, such that % convolvedFeatures(imageRow, imageCol, featureNum, imageNum) is the % value of the convolved featureNum feature for the imageNum image over % the region (imageRow, imageCol) to (imageRow + filterDim - 1, imageCol + filterDim - 1) % % Expected running times: % Convolving with 100 images should take less than 30 seconds % Convolving with 5000 images should take around 2 minutes % (So to save time when testing, you should convolve with less images, as % described earlier) for imageNum = 1:numImages for filterNum = 1:numFilters % convolution of image with feature matrix convolvedImage = zeros(convDim, convDim); % Obtain the feature (filterDim x filterDim) needed during the convolution %%% YOUR CODE HERE %%% filter = squeeze(W(:,:,filterNum)); % Flip the feature matrix because of the definition of convolution, as explained later filter = rot90(squeeze(filter),2); % Obtain the image im = squeeze(images(:, :, imageNum)); % Convolve "filter" with "im", adding the result to convolvedImage % be sure to do a 'valid' convolution %%% YOUR CODE HERE %%% convolvedImage = conv2(im,filter,'valid'); % Add the bias unit % Then, apply the sigmoid function to get the hidden activation %%% YOUR CODE HERE %%% convolvedImage = bsxfun(@plus,convolvedImage,b(filterNum)); convolvedImage = 1 ./ (1+exp(-convolvedImage)); convolvedFeatures(:, :, filterNum, imageNum) = convolvedImage; end end end
cnnPool.m
function pooledFeatures = cnnPool(poolDim, convolvedFeatures) %cnnPool Pools the given convolved features % % Parameters: % poolDim - dimension of pooling region % convolvedFeatures - convolved features to pool (as given by cnnConvolve) % convolvedFeatures(imageRow, imageCol, featureNum, imageNum) % % Returns: % pooledFeatures - matrix of pooled features in the form % pooledFeatures(poolRow, poolCol, featureNum, imageNum) % numImages = size(convolvedFeatures, 4); numFilters = size(convolvedFeatures, 3); convolvedDim = size(convolvedFeatures, 1); pooledFeatures = zeros(convolvedDim / poolDim, ... convolvedDim / poolDim, numFilters, numImages); % Instructions: % Now pool the convolved features in regions of poolDim x poolDim, % to obtain the % (convolvedDim/poolDim) x (convolvedDim/poolDim) x numFeatures x numImages % matrix pooledFeatures, such that % pooledFeatures(poolRow, poolCol, featureNum, imageNum) is the % value of the featureNum feature for the imageNum image pooled over the % corresponding (poolRow, poolCol) pooling region. % % Use mean pooling here. %%% YOUR CODE HERE %%% for imageNum = 1:numImages for featureNum = 1:numFilters featuremap = squeeze(convolvedFeatures(:,:,featureNum,imageNum)); pooledFeaturemap = conv2(featuremap,ones(poolDim)/(poolDim^2),'valid'); pooledFeatures(:,:,featureNum,imageNum) = pooledFeaturemap(1:poolDim:end,1:poolDim:end); end end end
computeNumericalGradient.m
function numgrad = computeNumericalGradient(J, theta) % numgrad = computeNumericalGradient(J, theta) % theta: a vector of parameters % J: a function that outputs a real-number. Calling y = J(theta) will return the % function value at theta. % Initialize numgrad with zeros numgrad = zeros(size(theta)); %% ---------- YOUR CODE HERE -------------------------------------- % Instructions: % Implement numerical gradient checking, and return the result in numgrad. % (See Section 2.3 of the lecture notes.) % You should write code so that numgrad(i) is (the numerical approximation to) the % partial derivative of J with respect to the i-th input argument, evaluated at theta. % I.e., numgrad(i) should be the (approximately) the partial derivative of J with % respect to theta(i). % % Hint: You will probably want to compute the elements of numgrad one at a time. epsilon = 1e-4; for i =1:length(numgrad) oldT = theta(i); theta(i)=oldT+epsilon; pos = J(theta); theta(i)=oldT-epsilon; neg = J(theta); numgrad(i) = (pos-neg)/(2*epsilon); theta(i)=oldT; if mod(i,100)==0 fprintf('Done with %d\n',i); end; end; %% --------------------------------------------------------------- end
minFuncSGD.m
function [opttheta] = minFuncSGD(funObj,theta,data,labels,... options) % Runs stochastic gradient descent with momentum to optimize the % parameters for the given objective. % % Parameters: % funObj - function handle which accepts as input theta, % data, labels and returns cost and gradient w.r.t % to theta. % theta - unrolled parameter vector % data - stores data in m x n x numExamples tensor % labels - corresponding labels in numExamples x 1 vector % options - struct to store specific options for optimization % % Returns: % opttheta - optimized parameter vector % % Options (* required) % epochs* - number of epochs through data % alpha* - initial learning rate % minibatch* - size of minibatch % momentum - momentum constant, defualts to 0.9 %%====================================================================== %% Setup assert(all(isfield(options,{'epochs','alpha','minibatch'})),... 'Some options not defined'); if ~isfield(options,'momentum') options.momentum = 0.9; end; epochs = options.epochs; alpha = options.alpha; minibatch = options.minibatch; m = length(labels); % training set size % Setup for momentum mom = 0.5; momIncrease = 20; velocity = zeros(size(theta)); %%====================================================================== %% SGD loop it = 0; for e = 1:epochs % randomly permute indices of data for quick minibatch sampling rp = randperm(m); for s=1:minibatch:(m-minibatch+1) it = it + 1; % increase momentum after momIncrease iterations if it == momIncrease mom = options.momentum; end; % get next randomly selected minibatch mb_data = data(:,:,rp(s:s+minibatch-1)); mb_labels = labels(rp(s:s+minibatch-1)); % evaluate the objective function on the next minibatch [cost grad] = funObj(theta,mb_data,mb_labels); % Instructions: Add in the weighted velocity vector to the % gradient evaluated above scaled by the learning rate. % Then update the current weights theta according to the % sgd update rule %%% YOUR CODE HERE %%% velocity = mom*velocity+alpha*grad; % 见ufldl教程Optimization: Stochastic Gradient Descent theta = theta-velocity; fprintf('Epoch %d: Cost on iteration %d is %f\n',e,it,cost); end; % aneal learning rate by factor of two after each epoch alpha = alpha/2.0; end; opttheta = theta; end
cnnInitParams.m
function theta = cnnInitParams(imageDim,filterDim,numFilters,... poolDim,numClasses) % Initialize parameters for a single layer convolutional neural % network followed by a softmax layer. % % Parameters: % imageDim - height/width of image % filterDim - dimension of convolutional filter % numFilters - number of convolutional filters % poolDim - dimension of pooling area % numClasses - number of classes to predict % % % Returns: % theta - unrolled parameter vector with initialized weights %% Initialize parameters randomly based on layer sizes. assert(filterDim < imageDim,'filterDim must be less that imageDim'); Wc = 1e-1*randn(filterDim,filterDim,numFilters); outDim = imageDim - filterDim + 1; % dimension of convolved image % assume outDim is multiple of poolDim assert(mod(outDim,poolDim)==0,... 'poolDim must divide imageDim - filterDim + 1'); outDim = outDim/poolDim; hiddenSize = outDim^2*numFilters; % we'll choose weights uniformly from the interval [-r, r] r = sqrt(6) / sqrt(numClasses+hiddenSize+1); Wd = rand(numClasses, hiddenSize) * 2 * r - r; bc = zeros(numFilters, 1); bd = zeros(numClasses, 1); % Convert weights and bias gradients to the vector form. % This step will "unroll" (flatten and concatenate together) all % your parameters into a vector, which can then be used with minFunc. theta = [Wc(:) ; Wd(:) ; bc(:) ; bd(:)]; end
cnnParamsToStack.m
function [Wc, Wd, bc, bd] = cnnParamsToStack(theta,imageDim,filterDim,... numFilters,poolDim,numClasses) % Converts unrolled parameters for a single layer convolutional neural % network followed by a softmax layer into structured weight % tensors/matrices and corresponding biases % % Parameters: % theta - unrolled parameter vectore % imageDim - height/width of image % filterDim - dimension of convolutional filter % numFilters - number of convolutional filters % poolDim - dimension of pooling area % numClasses - number of classes to predict % % % Returns: % Wc - filterDim x filterDim x numFilters parameter matrix % Wd - numClasses x hiddenSize parameter matrix, hiddenSize is % calculated as numFilters*((imageDim-filterDim+1)/poolDim)^2 % bc - bias for convolution layer of size numFilters x 1 % bd - bias for dense layer of size hiddenSize x 1 outDim = (imageDim - filterDim + 1)/poolDim; hiddenSize = outDim^2*numFilters; %% Reshape theta indS = 1; indE = filterDim^2*numFilters; Wc = reshape(theta(indS:indE),filterDim,filterDim,numFilters); indS = indE+1; indE = indE+hiddenSize*numClasses; Wd = reshape(theta(indS:indE),numClasses,hiddenSize); indS = indE+1; indE = indE+numFilters; bc = theta(indS:indE); bd = theta(indE+1:end); end
cnnExercise.m
%% Convolution and Pooling Exercise % Instructions % ------------ % % This file contains code that helps you get started on the % convolution and pooling exercise. In this exercise, you will only % need to modify cnnConvolve.m and cnnPool.m. You will not need to modify % this file. %%====================================================================== %% STEP 0: Initialization and Load Data % Here we initialize some parameters used for the exercise. imageDim = 28; % image dimension filterDim = 8; % filter dimension numFilters = 100; % number of feature maps numImages = 60000; % number of images poolDim = 3; % dimension of pooling region % Here we load MNIST training images addpath ../common/; images = loadMNISTImages('../common/train-images-idx3-ubyte'); images = reshape(images,imageDim,imageDim,numImages); W = randn(filterDim,filterDim,numFilters); b = rand(numFilters); %%====================================================================== %% STEP 1: Implement and test convolution % In this step, you will implement the convolution and test it on % on a small part of the data set to ensure that you have implemented % this step correctly. %% STEP 1a: Implement convolution % Implement convolution in the function cnnConvolve in cnnConvolve.m %% Use only the first 8 images for testing convImages = images(:, :, 1:8); % NOTE: Implement cnnConvolve in cnnConvolve.m first! convolvedFeatures = cnnConvolve(filterDim, numFilters, convImages, W, b); %% STEP 1b: Checking your convolution % To ensure that you have convolved the features correctly, we have % provided some code to compare the results of your convolution with % activations from the sparse autoencoder % For 1000 random points for i = 1:1000 filterNum = randi([1, numFilters]); imageNum = randi([1, 8]); imageRow = randi([1, imageDim - filterDim + 1]); imageCol = randi([1, imageDim - filterDim + 1]); patch = convImages(imageRow:imageRow + filterDim - 1, imageCol:imageCol + filterDim - 1, imageNum); feature = sum(sum(patch.*W(:,:,filterNum)))+b(filterNum); feature = 1./(1+exp(-feature)); if abs(feature - convolvedFeatures(imageRow, imageCol,filterNum, imageNum)) > 1e-9 fprintf('Convolved feature does not match test feature\n'); fprintf('Filter Number : %d\n', filterNum); fprintf('Image Number : %d\n', imageNum); fprintf('Image Row : %d\n', imageRow); fprintf('Image Column : %d\n', imageCol); fprintf('Convolved feature : %0.5f\n', convolvedFeatures(imageRow, imageCol, filterNum, imageNum)); fprintf('Test feature : %0.5f\n', feature); error('Convolved feature does not match test feature'); end end disp('Congratulations! Your convolution code passed the test.'); %%====================================================================== %% STEP 2: Implement and test pooling % Implement pooling in the function cnnPool in cnnPool.m %% STEP 2a: Implement pooling % NOTE: Implement cnnPool in cnnPool.m first! pooledFeatures = cnnPool(poolDim, convolvedFeatures); %% STEP 2b: Checking your pooling % To ensure that you have implemented pooling, we will use your pooling % function to pool over a test matrix and check the results. testMatrix = reshape(1:64, 8, 8); expectedMatrix = [mean(mean(testMatrix(1:4, 1:4))) mean(mean(testMatrix(1:4, 5:8))); ... mean(mean(testMatrix(5:8, 1:4))) mean(mean(testMatrix(5:8, 5:8))); ]; testMatrix = reshape(testMatrix, 8, 8, 1, 1); pooledFeatures = squeeze(cnnPool(4, testMatrix)); if ~isequal(pooledFeatures, expectedMatrix) disp('Pooling incorrect'); disp('Expected'); disp(expectedMatrix); disp('Got'); disp(pooledFeatures); else disp('Congratulations! Your pooling code passed the test.'); end
参考文献:
论文Notes on Convolutional Neural Networks, Jake Bouvrie
——





