Deep Learning 6_深度学习UFLDL教程：Softmax Regression_Exercise（斯坦福大学深度学习教程）

前言

练习内容：Exercise:Softmax Regression。完成MNIST手写数字数据库中手写数字的识别，即：用6万个已标注数据（即：6万张28*28的图像块（patches）），作训练数据集，然后利用其训练softmax分类器，再用1万个已标注数据（即：1万张28*28的图像块（patches））作为测试数据集，用前面训练好的softmax分类器对测试数据集进行分类，并计算分类的正确率。

注意：本实验中，只用原始数据本身作训练集，而并不是从原始数据中提取特征作训练集。

理论知识：Softmax回归和Deep learning：十三(Softmax Regression)，看softmax回归之前，最好看一下线性回归和逻辑回归。

优秀的编程技巧：

1. labels(labels==0) = 10; % 把标签0变为标签10，故labels的值是[1，10]，而原来是[0，9]

优点：这种写法不需要用if语句去检查labels中的每个值，而直接把labels中的0替换为10，效率很高，减少运行时间。

2. acc = mean(labels(:) == pred(:));%计算正确率

优点：让人眼前一亮的正确率计算方式，表达式labels(:) == pred(:)得到一个矩阵A，如元素labels(i)与pred(i)对应相等，刚A(i)为1，否则为0。然后再计算A的的平均值就得到了正确率。大牛的编程技巧太棒了，记得有一种说法：一个程序员的优秀程度，主要是看其代码的简洁程度。这种实现方式不仅表达简单，而且运行效率高。

3.
% 为加快梯度检查的效率，从而方便调试，可在调试时可减少输入数据大小。下面随机产生合成的数据集用于调试。
DEBUG = true; % Set DEBUG to true when debugging.
if DEBUG
inputSize = 8;
inputData = randn(8, 100);
labels = randi(10, 100, 1);
end

优点：这种写法、思想不错，方便调试。

4.防止溢出的技巧：

M = bsxfun(@minus,theta*data,max(theta*data, [], 1));% max(theta*data, [], 1)返回theta*data每一列的最大值，返回值为行向量
                                                     % theta*data的每个元素值都减去其对应列的最大值，即：把每一列的最大值都置为0了
                                                     % 这一步的目的是防止下一步计算指数函数时溢出

这种方法在以后的很多地方都可以看到，这里Ng特别介绍且用到了这一技巧。

一些matlab函数：

sparse函数

功能：Create sparse matrix-创建稀疏矩阵

用法1：S=sparse(X)——将矩阵X转化为稀疏矩阵的形式，即矩阵X中任何零元素去除，非零元素及其下标（索引）组成矩阵S。如果X本身是稀疏的，sparse(X)返回S。

例如：

A=
0 2 0
4 0 6
7 0 0

B=sparse(A)=

(2,1) 4
(3,1) 7
(1,2) 2
(2,3) 6

用法2：S = sparse(i,j,s,m,n,nzmax)——由i,j,s三个向量创建一个m*n的稀疏矩阵（上面的B矩阵形式），并且最多含有nzmax个元素。

例如：

B=sparse([1,2,3],[1,2,3],[0,1,2],4,4,4)

B =
(2,2) 1

(3,3) 2

其中i=[1,2,3]，稀疏矩阵的行位置；j=[1,2,3]，稀疏矩阵的列位置；s=[0,1,2]，稀疏矩阵元素值。其位置为一一对应。

m=4(>=max(i)),n=4(>=max(j)) (注：m和n的值可以在满足条件的范围内任意选取)，用于限定稀疏的大小。

nzmax=4(>=max(i or j))，稀疏矩阵最多可以有nzmax个元素。

一些简写的情况：

S = sparse(i,j,s,m,n)——nzmax = length(S) ；

S = sparse(i,j,s)——使m = max(i) 和 n = max(j)，在S中零元素被移除前计算最大值，[i j s]中其中一行可能为[m n 0]；

S = sparse(m,n)——sparse([],[],[],m,n,0)的缩写，生成一个m*n的所有元素都是0的稀疏矩阵。

应用举例：
S = sparse(1:n,1:n,1) 生成一个n*n的单位稀疏矩阵，和S = sparse(eye(n,n))有相同的结果，但是如果它的元素大部分是零元素的情况下也会暂时性的生成n*n的全矩阵。 book.iLoveMatlab.cn

B = sparse(10000,10000,pi) 可能不是非常有用的，但是它是能运行和允许的，它生成一个10000*10000的仅仅包含一个非零原色的矩阵，不要用full(B)，因为这需要800兆储存单元。

full函数

功能：把稀疏矩阵转为全矩阵

A=full(X)——把稀疏矩阵X转换为全矩阵存储形式A。

matlab sparse matrix和full matrix

其实这只是matlab中存储稀疏矩阵的两种方法。

MATLAB函数sparse简介
函数功能：
这个函数与稀疏矩阵有关。
先说MATLAB中两个概念：full storage organization（对应于full matrix）和sparse storage organization（对应于sparse matrix）。
而要说明这两个概念，需要介绍稀疏矩阵的概念。
一般意义上的稀疏矩阵，就是看起来很松散的，也就是说，在这个矩阵中，绝大多数元素是零。例如：
0, 0, 0, 0;
0, 0, 1, 0;
0, 0, 0, 0;
0, 1, 0, 2;
计算机存储稀疏矩阵可以有两种思路：
1.按照存储一个普通矩阵一样存储一个稀疏矩阵，比如上面这个稀疏矩阵中总共十六个元素（三个非零元素），把这些元素全部放入存储空间中。这种存储方式，在matlab就叫做full storage organization。
2.只存储非零元素，那么怎么存储呢？
(4,2)        1
(2,3)        1
(4,4)        2
看出来了吧，只存储非零元素在稀疏矩阵中的位置和值。比如，上面所举的这个例子，值为2的项在第4行第4列，那么我们就只需要存储这一非零项在稀疏矩阵中的“坐标”（4,4）和这一非零项的值2。在MATLAB中，这种存储方式就叫做sparse storage organization。虽然，这样要多存储一组坐标，但如果稀疏矩阵中非零元素非常少，以这种存储方式存储稀疏矩阵反而节省了内存空间。
为什么matlab中会同时存在这两种存储方式呢？
第一种方式，更加直观，进行矩阵运算时（比如稀疏矩阵的乘法），算法简单易实现。
而第二种方式，虽然有时可以节省存储数据时占用的存储空间，但进行运算时需要专门的算法实现（使用C语言编写过稀疏矩阵乘法的同学应该能体会到）。
sparse函数的功能就是把以第一种存储形式存储的稀疏矩阵转换成第二种形式存储（其实这个函数更重要的功能是构建稀疏矩阵，这里不再讨论）。对应的函数为full，即把以第二种方式存储的稀疏矩阵转换成第一种方式存储。
在MATLAB中，存储一个稀疏矩阵有两种方法。
语法格式：
S = sparse(A)
S = sparse(i,j,s,m,n,nzmax)
S = sparse(i,j,s,m,n)
S = sparse(i,j,s)
S = sparse(m,n)
各种语法格式详见MATLAB帮助文档。
相关函数：full、issparse
程序示例
>> A = [0, 0, 0, 0;
0, 0, 1, 0;
0, 0, 0, 0;
0, 1, 0, 2];
>> sparse(A)
ans =
   (4,2)        1
   (2,3)        1
   (4,4)        2

当然sparse函数还可以通过一定规则构造稀疏矩阵，这里就不多说了。

max函数

当A是一个列向量时候，返回一个最大值，在此不在赘述。

当Amxn是一个矩阵的时候，有以下几种情况：

① C = max(max(A))，返回矩阵最大值

② D = max(A,[],1)，返回每一行的最大值，即mx1的行向量

③ E = max(A,[],2)，返回每一列的最大值，即1xm的列向量

④ F = max(A,8)，当元素小于8，用8填充

⑤ [U V] = max(A)，返回行列最大元素的行号与列号

注意以下几个表达式：

H = max(A)

I = max(A(:))

J = max(A(:,:))

编程实验如下：

A = fix (rand (5,3)*50)%

B = A;%矩阵备份一次

C = max(max(A))%矩阵最值

D = max(A,[],1)%每一列的最值，得到行向量

E = max(A,[],2)%每一行的最值，得到列向量

F = max(A,8)%小于8的数替换成8

[U V] = max(A)%U为列极值，V为行号

H = max(A)%功能同D

I = max(A(:))%功能同C

J = max(A(:,:))%功能同D

softmax回归基本知识

代价函数为：

$\begin{align} J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }} \right] + \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^n \theta_{ij}^2 \end{align}$

代价函数梯度为：

$\begin{align} \nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j \end{align}$

实验步骤

1.初始化参数，加载训练数据集。注意：MNIST手写数字数据集所有图片的每个像素灰度值都已经被归一化到了[0，1]之间，所以将来如果是用自己的训练样本，不要忘记归一化像素值。

2.矢量化编程实现softmax回归的代价函数及其梯度，即softmaxCost.m文件。

3.利用computeNumericalGradient函数检查上一步中的梯度计算是否正确，该函数见Deep Learning一：Sparse Autoencoder练习（斯坦福大学UFLDL深度学习教程）。

4.用用L-BFGS算法训练softmax回归模型，得到模型softmaxModel，见softmaxTrain.m中的softmaxTrain函数

5.加载测试数据集，用上一步训练得到模型softmaxModel来对测试数据进行分类，得到分类结果（见softmaxPredict.m），然后计算正确率。

运行结果

Accuracy: 92.640%
Elapsed time is 15.591119 seconds.

注意：别忘记了Andrew Ng的提醒，他们自己的准确率有92.6%。如果你得到的准确率小于91%，请检查你的代码、训练数据集及其权重是否正确；如果你的准确率非常高，达到99%至100%时，你可能把测试数据集作为了训练数据集。

问题

1.在softmaxExercise.m中有如下一句代码：

images = loadMNISTImages('train-images.idx3-ubyte');
labels = loadMNISTLabels('train-labels.idx1-ubyte');
labels(labels==0) = 10; % 把标签0变为标签10，故labels的值是[1，10]，而原来是[0，9] ？为什么非要这样？

为什么非要把原来的标签0变为标签10呢？搞不懂！

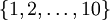在Exercise:Softmax Regression中是这样解释的：The images are pre-processed to scale the pixel values to the range $\{1, 2, \ldots, 10\}$

代码

softmaxCost.m

function [cost, grad] = softmaxCost(theta, numClasses, inputSize, lambda, data, labels)

% numClasses - 类别数量 the number of classes 
% inputSize - 输入数据大小 the size N of the input vector
% lambda - 权重衰减系数 weight decay parameter
% data -输入数据集 the N x M input matrix, where each column data(:, i) corresponds to
%        a single test set
% labels - 输入数据的标签 an M x 1 matrix containing the labels corresponding for the input data
%

% Unroll the parameters from theta
theta = reshape(theta, numClasses, inputSize);

numCases = size(data, 2);%输入数据集的数量

groundTruth = full(sparse(labels, 1:numCases, 1));%产生一个100*100的矩阵，它的第labels(i)行第i列的元素值为1，其余全为0，其中i为1到numCases，即：1到100
cost = 0;

thetagrad = zeros(numClasses, inputSize);

%% ---------- YOUR CODE HERE --------------------------------------
%  Instructions: Compute the cost and gradient for softmax regression.
%                You need to compute thetagrad and cost.
%                The groundTruth matrix might come in handy.

M = bsxfun(@minus,theta*data,max(theta*data, [], 1));% max(theta*data, [], 1)返回theta*data每一列的最大值，返回值为行向量
                                                     % theta*data的每个元素值都减去其对应列的最大值，即：把每一列的最大值都置为0了
                                                     % 这一步的目的是防止下一步计算指数函数时溢出
M = exp(M);
p = bsxfun(@rdivide, M, sum(M));
cost = -1/numCases * groundTruth(:)' * log(p(:)) + lambda/2 * sum(theta(:) .^ 2);
thetagrad = -1/numCases * (groundTruth - p) * data' + lambda * theta; 



% ------------------------------------------------------------------
% Unroll the gradient matrices into a vector for minFunc
grad = [thetagrad(:)];
end

softmaxPredict.m

 1 function [pred] = softmaxPredict(softmaxModel, data)
 2 
 3 % softmaxModel - model trained using softmaxTrain
 4 % data - the N x M input matrix, where each column data(:, i) corresponds to
 5 %        a single test set
 6 %
 7 % Your code should produce the prediction matrix 
 8 % pred, where pred(i) is argmax_c P(y(c) | x(i)).
 9  
10 % Unroll the parameters from theta
11 theta = softmaxModel.optTheta;  % this provides a numClasses x inputSize matrix
12 pred = zeros(1, size(data, 2));
13 
14 %% ---------- YOUR CODE HERE --------------------------------------
15 %  Instructions: Compute pred using theta assuming that the labels start 
16 %                from 1.
17 
18 [nop, pred] = max(theta * data);
19 %  pred= max(peed_temp);
20 
21 
22 
23 
24 
25 % ---------------------------------------------------------------------
26 
27 end

——

posted @ 2015-11-04 13:52 夜空中最帅的星阅读(2103) 评论(5) 编辑收藏举报

刷新页面返回顶部

夜空中最帅的星

Deep Learning 6_深度学习UFLDL教程：Softmax Regression_Exercise（斯坦福大学深度学习教程）

前言

实验步骤

问题

代码

公告