Deep Learning 3_深度学习UFLDL教程：预处理之主成分分析与白化_总结（斯坦福大学深度学习教程）

1PCA

    ①PCA的作用：一是降维；二是可用于数据可视化；

注意：降维的原因是因为原始数据太大，希望提高训练速度但又不希望产生很大的误差。

    ② PCA的使用场合：一是希望提高训练速度；二是内存太小；三是希望数据可视化。

    ③用PCA前的预处理：(1)规整化特征的均值大致为0；(2)规整化不同特征的方差值彼此相似。

    对于自然图片，即使不进行方差归一化操作，条件(2)也自然满足，故而我们不再进行任何方差归一化操作（对音频数据,如声谱,或文本数据,如词袋向量，我们通常也不进行方差归一化）。非自然图像有手写文字，或者白背景正中摆放单独物体等。

2白化（whitening）

    ①白化的作用：去掉数据之间的相关联度，是很多算法进行预处理的步骤。

    ②数据的whitening必须满足两个条件：一是不同特征间相关性最小，接近0；二是所有特征的方差相等（不一定为1）。常见的白化操作有PCA whitening和ZCA whitening。

PCA whitening：是指将数据x经过PCA转换为 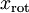 ，然后降维为  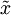后，可以看出  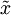中每一维是独立的，满足whitening白化的第一个条件，这是只需要将z中的每一维都除以标准差就得到了每一维的方差为1，也就是说方差相等，故PCA白化后的数据方差一定都为1。它主要用于降维、去除相关性。公式如下：

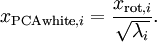
ZCA whitening：是指数据x先经过PCA变换为 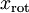 ，但是并不降维，因为这里是把所有的成分都选进去了。这是也同样满足whtienning的第一个条件，特征间相互独立。然后同样进行方差为1的操作，最后将得到的矩阵左乘一个特征向量矩阵U即可，故ZCA白化后的数据方差并不为1但都相等。它主要用于去除相关性且尽量保持原始数据。公式如下：

 

 

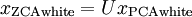
参考资料：

UFLDL

http://www.cnblogs.com/tornadomeet/archive/2013/03/21/2973231.html