2017-2018 20172309 《程序设计与数据结构(下)》第七章学习总结
2017-2018 20172309 《程序设计与数据结构(下)》第七章学习总结
一、教材学习内容总结
1.1关于二叉查找树的一些概念
- 二叉查找树具有附加属性,其左孩子小于父节点、而父节点又小余或者等于右结点。
- 因此二叉查找树的最右侧会存放最大元素、而其最左侧会存放最小元素。
- 二叉查找树是二叉树的扩展,它绝大数方法都会用到递归,二叉查找树的平均查找深度为O(log2N).
1.2实现二叉查找树
- 添加元素(addElement操作)
- 插入方法首先在插入的时候判断被插入元素的类型是不是Comparable类
if (!(element instanceof Comparable)),如果不是则会抛出NoComparableException -
- 如果根结点为null,被插入元素成为根结点。
-
- 根结点不为null,将使用
comparaTo()方法与TargetElement进行比较,
- 根结点不为null,将使用
-
- 得到的结果为-1、1时,分别放在父节点的左子树、和右子树。
-
- 然后继续跟接下来的结点进行比较,即重复步骤a、b、c。
- 就像这样:

- 插入方法首先在插入的时候判断被插入元素的类型是不是Comparable类
- 删除操作(removeElement操作)
- 删除操作将在二叉查找树中删除给定的Comparable元素,如果找不到、将抛出
ElemenNotFoundException. - 查找到要删除的元素之后删除操作分为三种情况:
-
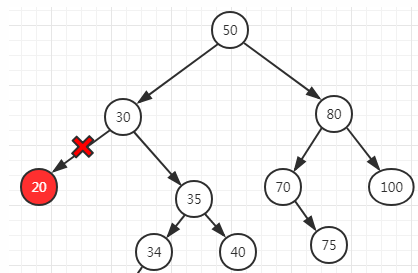
没有左右子节点,可以直接删除这个结点。比如删除结点20.
-
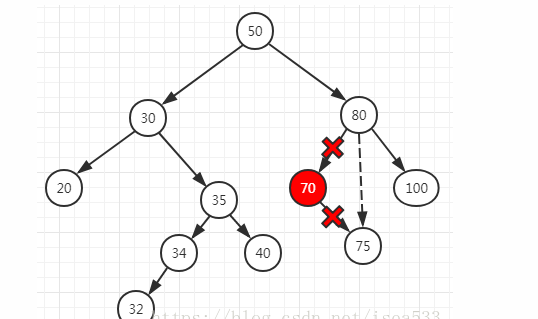
存在左节点或者右节点,删除该节点后其父结点与子节点连接。比如删除结点70。
-
同时存在左右子节点,将用其右子树中最小的结点与之交换。比如删除结点30.
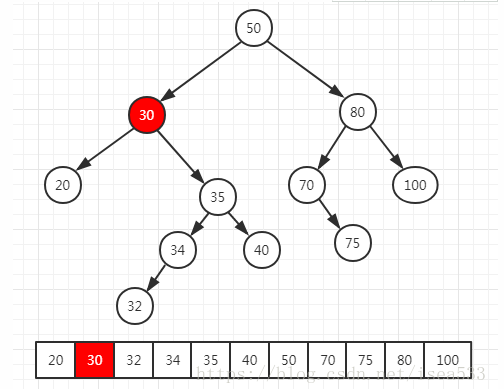
- 当我们将上面的二叉查找树使用中序遍历遍历时,得到的结果为上面的链表。
- 当我们删除结点30的时候,链表中32之后的所有结点都将往前移动一个位置,而且结点32是结点30之后的结点中最小的一个,因此它将成为代替被删除的那个结点。即:
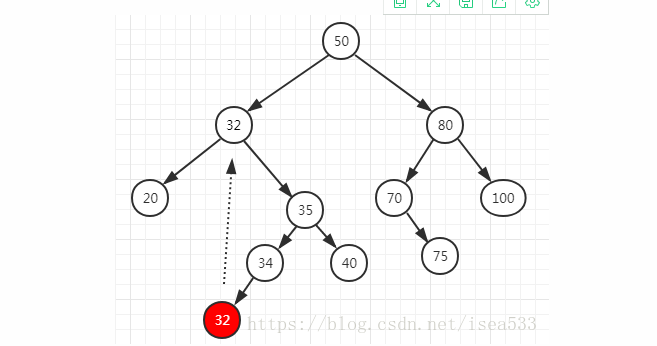
- 结点替换后,原来的结点32将被删除。
-
- 删除操作将在二叉查找树中删除给定的Comparable元素,如果找不到、将抛出
- removeAllOccurrences、removeMin、removeMax、findMax、findMin方法都在:LinkedBinarySearchTree类
1.3用有序列表实现二叉树
- 树的作用之一是为其他集合提供高效的实现。
- 树的使用实现集合会让有些操作变得高效,也会让一些操作变得低效:
| 操作 | LinkList | BinarySearchTreeList |
|---|---|---|
| removeFirst | O(1) | O(n) |
| removeLast | O(n) | O(n) |
| remove | O(n) | O(n) |
| first | O(1) | O(n) |
| last | O(n) | O(n) |
| contains | O(n) | O(n) |
| isEmpty | O(1) | O(1) |
| size | O(1) | O(1) |
| add | O(n) | O(n) |
黑色加粗代表使用树后操作将变得低效。
红色字体代表该操作可能使树变得不平衡。
1.4AVL树
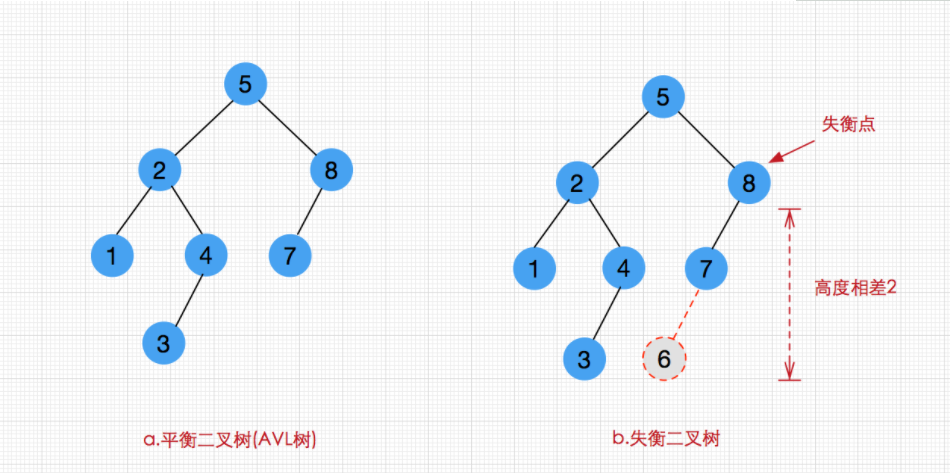
- 二叉查找树的平衡很重要!不平衡时,当我们插入一个已经排好序的一组数字时,它会变成一个类似于链表的结构。如图:
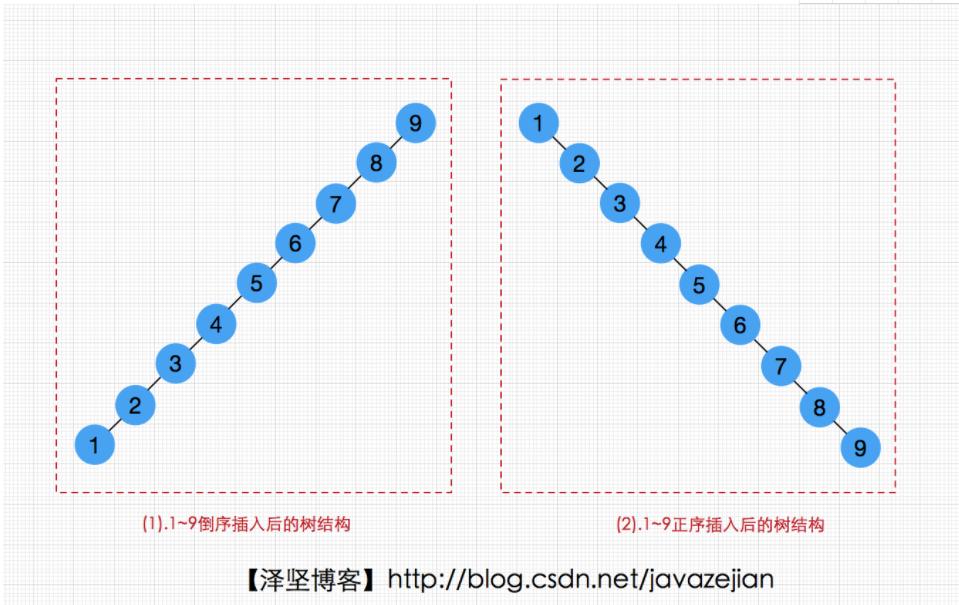
如果查找二叉树不平衡,其效率可能比线性结构还要低!因为每个结点还有额外的开销。 - 要解决这个问题,我们有如下规定: 任何结点不得过深,即:任何结点的平衡因子的绝对值不能超过1;(平衡因子:左子树的高度减去右子树的高度)
- 几个例子如下图:
- AVL树的插入操作首先会按照普通搜索二叉树的插入操作进行,当插入一个数据后,我们会沿着插入数据时所经过的的节点回溯,回溯的过程中会判回溯路径中的每个节点的左子支高度与右子支高度之差的绝对值是否超过1,如果超过1我们就进行调整,调整的目的是使得该节点满足AVL树平衡的定义。调整的情况可以分为以下四旋转操作。
- 左旋:以某一个节点为轴,它的右子枝逆针旋转,作为新子树的根,我们称之为左旋。
- 节点X右子支比左子支高度大2,且插入的节点位于节点X右孩子节点XR的右子支上。
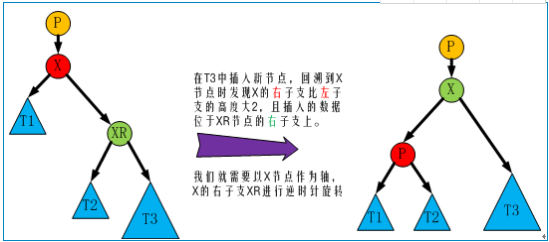
- 节点X右子支比左子支高度大2,且插入的节点位于节点X右孩子节点XR的右子支上。
- 右旋:以某一个节点为轴,它的左子枝顺时针旋转,作为新子树的根,我们称之为右旋。
- 节点X左子支比右子支高度大2,且插入的节点位于X的左孩子节点XL的左子支上。

- 节点X左子支比右子支高度大2,且插入的节点位于X的左孩子节点XL的左子支上。
- 左右旋:先经过一次左旋,然后经过一次右旋。
- 节点X左子支比右子支高度大2,且插入的节点位于节点X左孩子节点XL的右子支上。
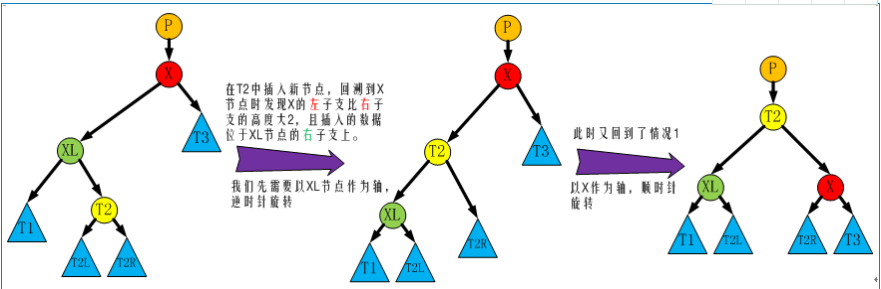
- 节点X左子支比右子支高度大2,且插入的节点位于节点X左孩子节点XL的右子支上。
- 右左旋:先经过一次右旋,再经过一次左旋。
- 节点X左子支比右子支高度大2,且插入的节点位于节点X左孩子节点XL的右子支上
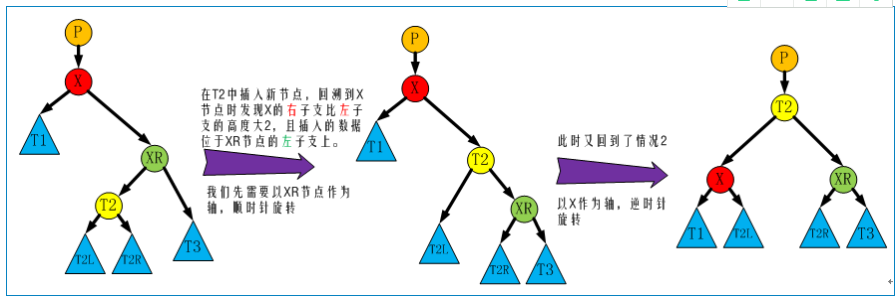
- 节点X左子支比右子支高度大2,且插入的节点位于节点X左孩子节点XL的右子支上
- 左旋:以某一个节点为轴,它的右子枝逆针旋转,作为新子树的根,我们称之为左旋。
- AVL树的实现:BinaryAVLTree
- 关于红黑树
- 见下面教材中的问题。
二、教材学习中的问题和解决过程
- 问题1:如何理解红黑树?它的功能AVL树也能实现,要这玩意儿干嘛?
- 问题1解决方案:
- 认识红黑树:(书中的什么概念就不说了,就说说自己的理解吧。)红黑树的特点是需要进行复杂的颜色变化、以及在AVL树中的旋转,但是它的出现解决了AVL树维护慢、空间开销大的不足。
- 现在我们来总结红黑树与AVL树的区别吧!
- AVL树又称为平衡二叉搜索树,他是一棵空树或者两子树的高度差绝对值不超过1.而红黑树用颜色标识高度,不是严格平衡的!
- 虽然AVL树的效率很高,但红黑树的效率更高。(例如:当进行删除操作而引起树不平衡时,AVL树最坏情况下需要维护从该节点到根结点所有节点的平衡,因而旋转的量级为(log2 N);而红黑树对于任何不平衡最多只需要旋转三次!)。
- 红黑树的查询性稍微逊色于AVL树,因为它比AVL树会稍微不平衡多一层,也就是说他会比AVL树多进行一次比较。
- 总而言之,他虽然复杂,但是它的效率总的来说比AVL树高。
代码调试中的问题和解决过程
-
问题1:在网上看代码时,发现了个问题:comparator中的comparable方法与平时用的comparaTo方法的异同点?
-
问题1解决方案:
- comparator这个东西是在网上看别人代码时看到的,他是作为一个比较器,我当时的疑问是为啥要这个东西,用ComparaTO这个方法不就好了么?如图:
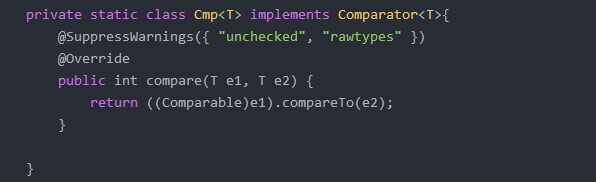
在之后的实验中我没有写这个构造器,准备使用ComparaTO方法,然后发现:
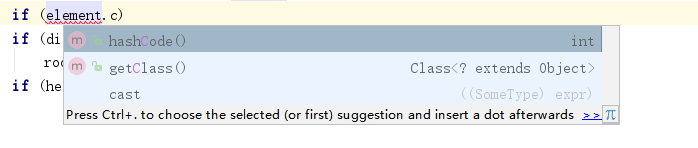
调用不了ComparaTO方法,是因为只能这样用String1.comparaTO(String2)...,也就是只能比较String类型。要想比较其他类型,就得写一个比较器,其中用Compara(T value1,T value2)方法。
- comparator这个东西是在网上看别人代码时看到的,他是作为一个比较器,我当时的疑问是为啥要这个东西,用ComparaTO这个方法不就好了么?如图:
-
问题2:如何实现左旋和右旋?
-
问题2解决方案:
- 额,这个东西书好像是看懂了,但是敲起代码来并没有那么容易,然后到网上找了找,根据是由有parent(是否是双指针)分为两种。
- 第一种:有parent:
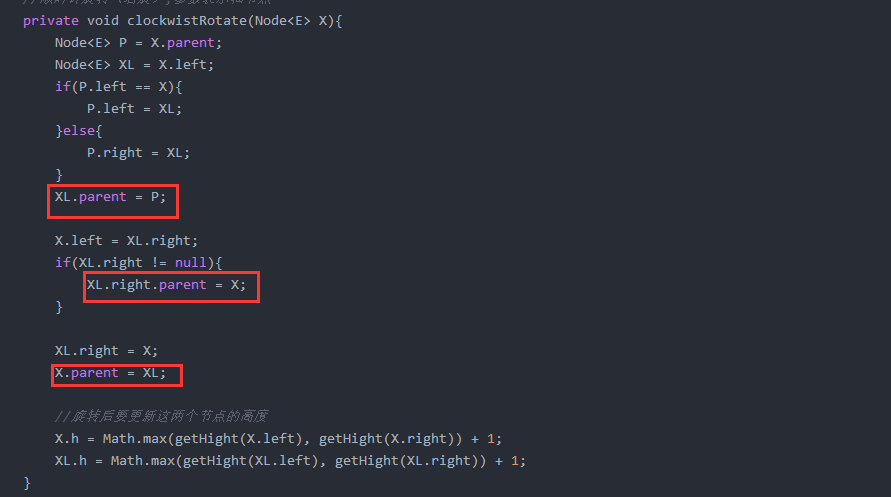
这种方法,每一次当父节点指向新的子节点时,子节点也要指向父节点。 - 第二种:没有parent:

这种没有parent指针的方法,虽然看起来简单,但当它不能调用叔叔结点!有parent指针的可以,比如:
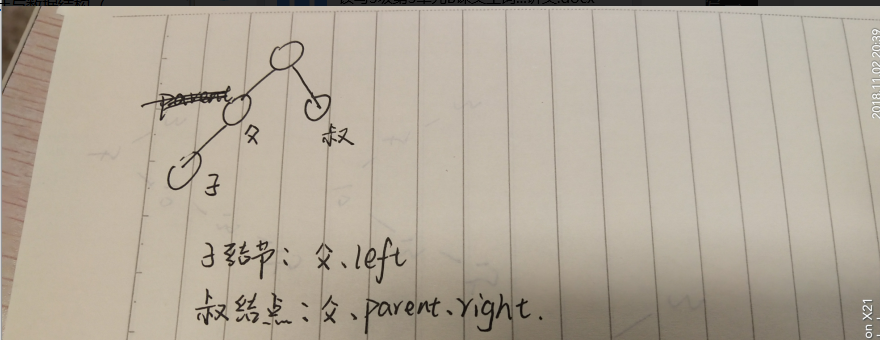
-
问题三:在二叉查找树中添加元素时,当添加已有元素或者添加两个相同元素时会发生什么情况?当添加比它小的元素时,这个小的元素会出现在这两个相同元素的左边?(比如添加了两个相同的元素5后,在添加一个元素3,那么这个3在哪个5的左边?)
-
问题3解决方案:
对于添加已有结点或相同结点可以分类讨论:- 一:当添加已有结点时,后来的数据之间覆盖原来的数据,有可能人说这个没有用,在我看来,当一个节点有两个数据时,这就变得非常有用,比如这两个数据是:name、price。
已有的数据为:name:牛奶 、price:2元
后来的数据为:name:牛奶 、 price:2.5 元
一般来说、在实际生活中的应用一个节点会有很多数据,所以一般不会全部相同的。因此更新尤为重要。- 二:在书中代码上,数据不会更新的。相同的元素会放在原元素的右结点上,当放上比他小的元素时,会存在于它的第一个出现的结点的左节点上。
代码托管

上周考试错题总结
- 本周错题暂没出答案!
点评模板:
博客或代码中值得学习的或问题:
- 队友对于自己不懂得问题懂得深究,比如同学、百度。
- 队友的事比我多、学习java的效率比我高。
- 队友很细心、能够发现一些小问题。
点评过的同学博客和代码
其他(感悟、思考等,可选)
在上一章中,我说那一章很难。现在想是我错了!这个十一章是难的我脑壳都疼!特别是那个AVL、红黑树,哎。我得看代码去了····
学习进度条(上学期截止7200)
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 260/0 | 1/1 | 05/05 | |
| 第二周 | 300/560 | 1/2 | 13/18 | |
| 第三周 | 212/772 | 1/4 | 21/39 | |
| 第四周 | 330/1112 | 2/7 | 21/60 | |
| 第五周 | 1321/2433 | 1/8 | 30/90 | |
| 第六周 | 1024/3457 | 1/9 | 20/110 | |
| 第七周 | 900/4357 | 1/9 | 20/130 |