2017-2018 20172309第六章学习总结
2017-2018 20172309第六章学习总结
一、教材学习内容总结
-
什么是树?
- 栈、队列、列表都是线性结构,而树是非线性结构。
- 线性结构是一对一的,而树的特点是一对多。
- 树由一个包含结点和边的集组成。
- 结点与结点之间的连接是由边完成的。
- 位于树中较低层次的结点是上一层结点的孩子,没有任何孩子的结点称为叶子。
- 两个结点之间边的个数为其之间的路径长度。
- 树的高度是指根到叶子之间最远路径的长度。
- 用图表示:

-
树的分类:
-
树中任一结点可以具有最大孩子的数目,称为度,按照这个分类标准可分为:广义树、n元树、二叉树。
-
平衡树:树中所有叶子都位于同一层次或者至少是彼此相差不超过一个层。一个含有m个元素的平衡n元树具有的高度为logn(m)。
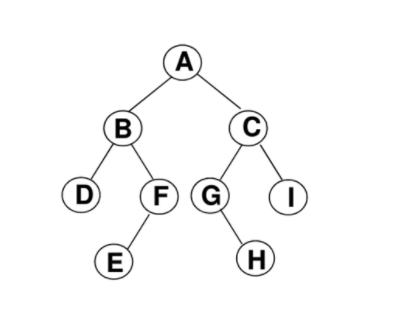
-
完全树:树是平衡的,且所有叶子都位于左边。
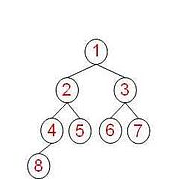
-
满树:n元树的所有叶子都位于同一层且每一结点要么是一片叶子要么正好具有n个孩子。
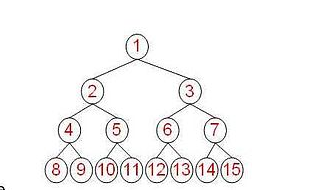
-
-
实现树的策略:
- 树的数组实现之计算策略:
这种计算策略是将元素n的左孩子放置于`2n+ 1`、右孩子放置于`2n+2`.其中,n是其双亲的索引。
举个例子:
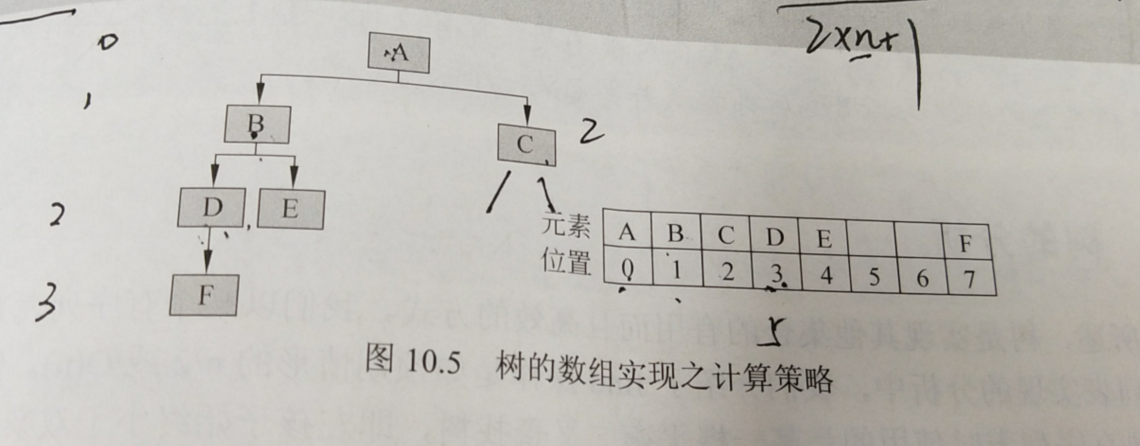
A的索引为0,B为A的左孩子,所以它在数组中的位置在
2*0+1=1,所以B在数组中的位置在索引为1的位置。D为B的左孩子,B的索引为1,所以D的索引为2*1+1=3.
- 树的数组实现之模拟链接策略:
数组中的每个元素都是一个结点,结点中储存了每一个孩子的索引,比如下图中A的孩子有两个B与C,他们的索引分别是2和1,因此2和1就被储存在了A中。
-
树的遍历:树的遍历主要有4种基本方法:前序遍历、中序遍历、后序遍历和层序遍历。
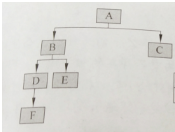
- 前序遍历:从根节点开始,访问每一个节点及其孩子。比如在上图的遍历顺序为:A、B、D、F、E、C。用伪代码实现为:
Visit node; Traverse(left child); Traverse(right child);- 中序排序:从根节点开始,访问结点的左孩子,然后是该结点,再然后是剩余任何结点。上图的遍历顺序为:D、B、E、F、A、C用伪代码实现为:
Traverse(left child); Visit node; Traverse(right child);- 后续遍历:从根结点开始,访问结点的孩子,然后是该结点。上图的遍历顺序为:F、D、E、B、C、A。用伪代码实现为:
Traverse(left child); Traverse(right child); Visit node;- 层序遍历:从根结点开始,访问每一层的所有的结点,一次一层。上图的遍历顺序为:A、B、C、D、E、F。
-
二叉树:二叉树是一种非常重要的数据结构,它同时具有数组和链表各自的特点:它可以像数组一样快速查找,也可以像链表一样快速添加。但是他也有自己的缺点:删除操作复杂。
二叉树的性质:
- 在二叉树的第i层上至多有2^(i-1)个结点。
- 深度为k的二叉树至多有2^k-1个结点(k≥1),最少有k个结点。
- 对任何一颗二叉树,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
- 具有n个节点的完全二叉树的深度为[log2n]+1,其中[log2n]+1是向下取整。
- 如果有一颗有n个节点的完全二叉树的节点按层次序编号,对任一层的节点i(1<=i<=n)有:
- 如果i=1,则节点是二叉树的根,无双亲,如果i>1,则其双亲节点为[i/2],向下取整
- 如果2i>n那么节点i没有左孩子,否则其左孩子为2i.
- 如果2i+1>n那么节点没有右孩子,否则右孩子为2i+1.
-
实现二叉树:
- 编写二叉树的接口(interface)BinaryTreeADT
:
- 使用二叉树:
- 用链表实现二叉树:
- 编写二叉树的接口(interface)BinaryTreeADT
二、教材学习中的问题和解决过程
- 问题1:跟据中序遍历的定义:从根结点开始,访问结点的左孩子,然后是该结点,再然后是任何剩余的结点。那么当一个节点只有一个孩子的时候,此时没有左右孩子之分。那么是先访问该结点的孩子,还是先访问其他结点?如图:当结点为D时,时先访问H,还是访问E。
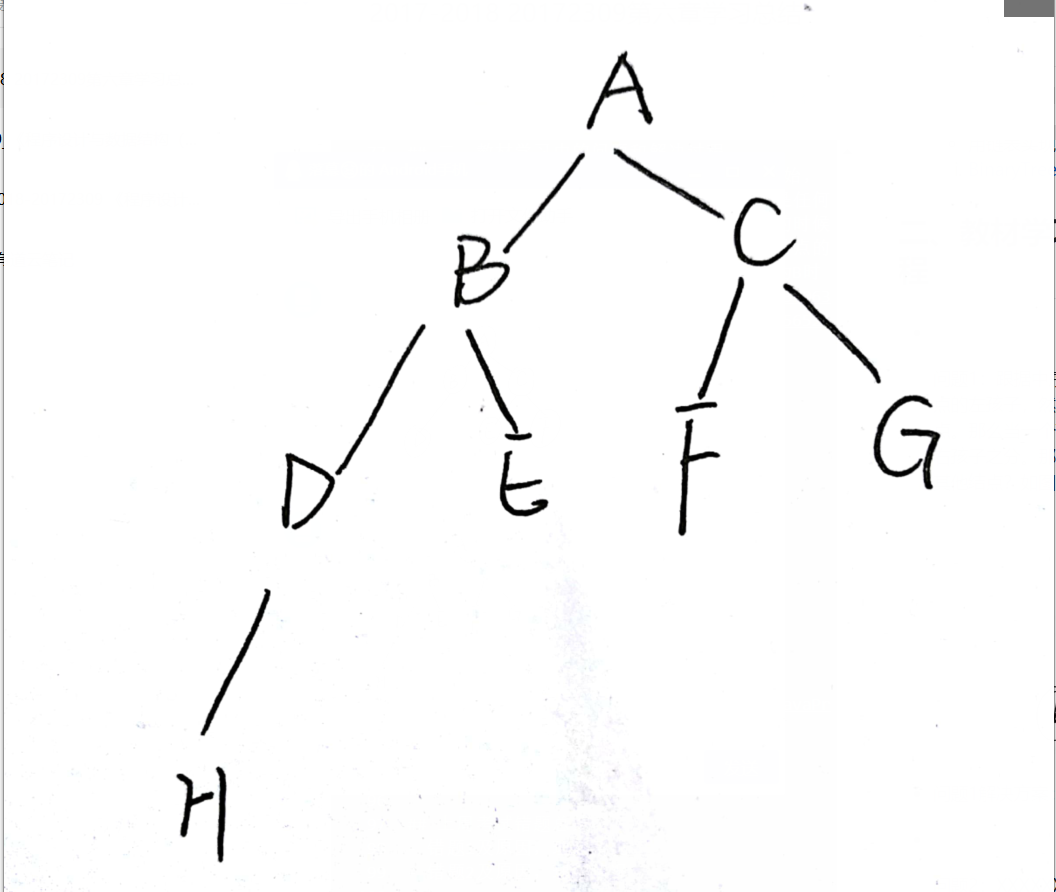
- 我的理解:对于D来说,虽然结点H不是其左孩子,但是对于D来说H、E都是他的剩余结点,然而H还是他的孩子,所以H还是有优先权的。因此上图的排列顺序为:H、D、B、E、A、F、C、G。
- 问题2:表达式树中的打印树PrintTree()是什么原理?
- 问题2解决方案:
这是一个打印树的方法:其中while循环每打印一个节点循环一次。举个例子2 × 3(表达式树状)- 首先说明:
- nodes:定义一个列表,用来装结点。
- levelList:定义一个列表用来装结点的层级。
- printDepth:树的深度(从零开始数)。
- countNode:用于记录输出结点的个数。
- currentLevel:当前结点的层级。
- previousLevel:之前结点的层级。
- result为输出结果。
- 在第一次循环之前:
- nodes:×//里面装有root结点,即“×”
- printDepth=1,possibleBodes=4,countNodes=0,currentLevel=0,previouslevel=-1,
- LevelList:0//里面装有0
- 第一次循环:
- countNodes=1;
- current=node(“×”),此时nodes=null;
- currentLevel= 0,此时LevelList=null;
- 进入if()语句,出来后result=“__”,previousLevel=0;(注:即只增加了一个空格,换行符自动省略。)
- 进入下一个if()语句,出来后:result=“__”+ "×";node:2 3;LevelList:1 1;
- 第二次循环:
- countNodes=2;
- current=node(“2”),此时nodes:3;
- currentLevel=1,此时LevelList:1;
- 进入if()语句,出来后result=“__”+“×”+“\n”,previousLevel=1;(注:此次增加的空格为0个,换行符自动省略。)
- 进入下一个if()语句,出来后:result=“__”+"×"+"\n"+2;node:3,null,null;LevelList:1,2,2;//这次因为结点2没有左孩子和右孩子,所以nodes进去了两个null,他们的层级为2.
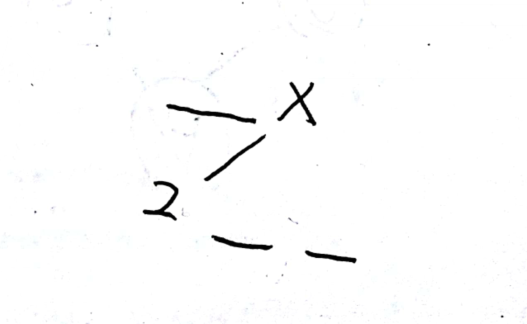
- 第三次循环:
- countNodes=3;
- current=node(“3”),此时nodes:null,null;
- currentLevel=1,此时LevelList:2,2;
- 进入if()语句,条件不满足,进入else。出来后result="—"+“×”+"\n\n"+"2"+"—"+"—",previousLevel=1;(注:此次增加的空格为2个。)
- 进入下一个if()语句,出来后:result="—"+“×”+"\n\n"+"2"+"—"+"—"+"3";node:null,null,null,null;LevelList:,2,2,2,2;//这次因为结点3没有左孩子和右孩子,所以nodes进去了两个null,他们的层级为2.
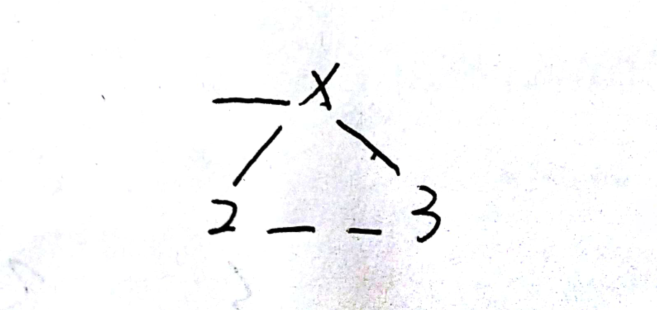
- 第四次循环:此后打印出来的都是null,看不到,因此不用讨论。
代码运行截图:
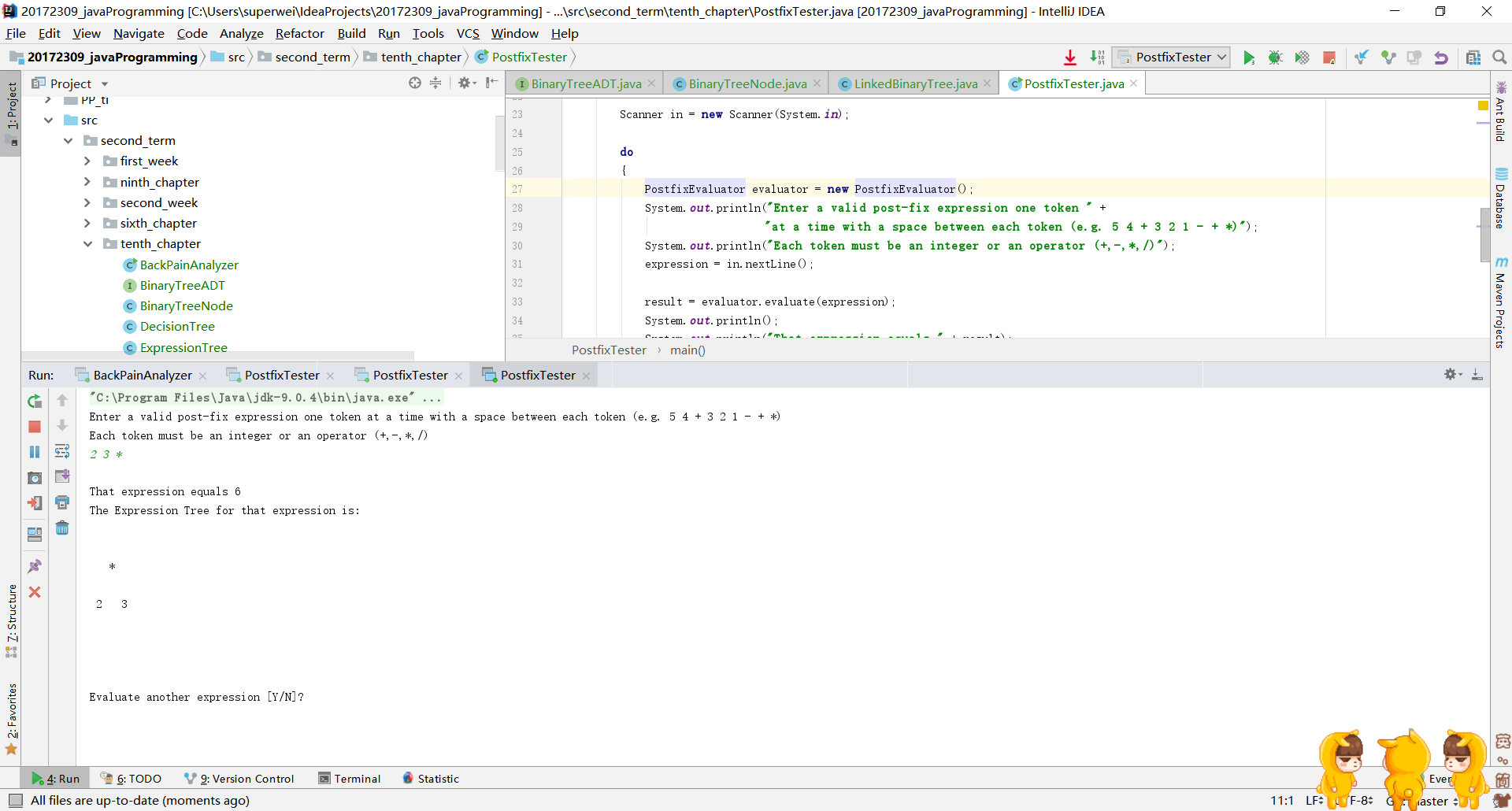
方法代码:
- 首先说明:
public String printTree() //打印树的代码。
{
UnorderedListADT<BinaryTreeNode<ExpressionTreeOp>> nodes =
new UnorderedListArrayList<BinaryTreeNode<ExpressionTreeOp>>();//定义一个列表,用来装结点。
UnorderedListADT<Integer> levelList =
new UnorderedListArrayList<Integer>();//定义一个列表用来装结点的层级。
BinaryTreeNode<ExpressionTreeOp> current;
String result = "";
int printDepth = this.getHeight();
int possibleNodes = (int)Math.pow(2, printDepth + 1);
int countNodes = 0;
nodes.addToRear(root);
Integer currentLevel = 0;
Integer previousLevel = -1;
levelList.addToRear(currentLevel);
while (countNodes < possibleNodes)
{
countNodes = countNodes + 1;
current = nodes.removefirst();
currentLevel = levelList.removefirst();
if (currentLevel > previousLevel)
{
result = result + "\n\n";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
result = result + " ";
}
else
{
for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)
{
result = result + " ";
}
}
if (current != null)
{
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
}
else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
return result;
}
- 问题三:LinkBinaryTree中要写迭代器的方法,如何写?
- 问题3的解决方法:关于第七章的迭代器,因为这个要写这个方法。所以先把相关知识总结一下:
- 首先来看看Java中的Iterator接口是如何实现的:
package java.util; public interface Iterator<E> { boolean hasNext();//判断是否存在下一个对象元素 E next();//获取下一个元素 void remove();//移除元素 }- Iterable:
- Java中还提供了一个Iterable接口,Iterable接口实现后的功能是‘返回’一个迭代器
- 用代码实现:
Package java.lang; import java.util.Iterator; public interface Iterable<T> { Iterator<T> iterator(); } - 还可以用来遍历集合中的元素。
还可以用for——each循环实现:Iterator<Book> itr = myList.iterator(); while(ite.hasnext()); System.out.println(itr.next());for(Book book:myList)//这两种方法是一样的。 System.out.println(book);- 还值得注意的是:Iterator遍历时不可以删除集合中的元素!
- 在使用Iterator的时候禁止对所遍历的容器进行改变其大小结构的操作。例如: 在使用Iterator进行迭代时,如果对集合进行了add、remove操作就会出现ConcurrentModificationException异常。
- 因为在你迭代之前,迭代器已经被通过list.itertor()创建出来了,如果在迭代的过程中,又对list进行了改变其容器大小的操作,那么Java就会给出异常。因为此时Iterator对象已经无法主动同步list做出的改变,Java会认为你做出这样的操作是线程不安全的,就会给出善意的提醒(抛出ConcurrentModificationException异常)
代码调试中的问题和解决过程
- 问题1:在测试pp项目代码正确性时,出现
Exception in thread "main" java.lang.ClassCastException: java.base/java.lang.Integer cannot be cast to second_term.tenth_chapter.ExpressionTree - 问题1解决方案:出现上面的问题的原因是:在LinkedBinaryTree中的toString方法中的:
UnorderedListADT<BinaryTreeNode<ExpressionTree>> nodes =
new UnorderedListArrayList<BinaryTreeNode<ExpressionTree>>();
UnorderedListADT<Integer> levelList =
new UnorderedListArrayList<Integer>();
BinaryTreeNode<ExpressionTree> current;
里面应该用泛型:所以把Expressiontree改为T就OK了。
运行截图为:
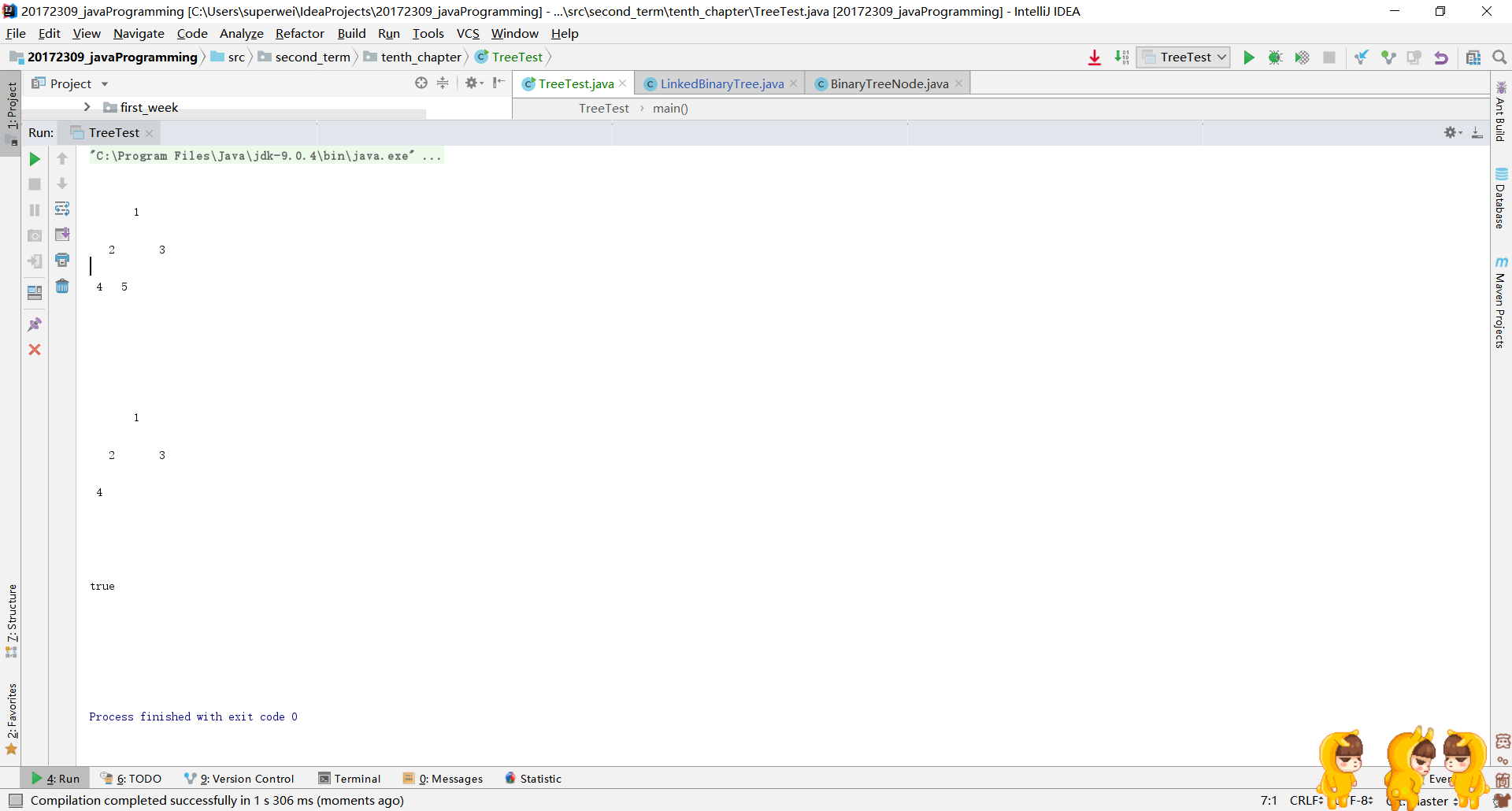
代码托管

上周考试错题总结
- 错题1:
_________ traversal means visit the left child, then the node, then the right child.
A .preorder
B .postorder
C .inorder
D .level-order - 理解情况:
- 中序排序:先访问左孩子,然后是该节点,再然后是任何结点。
- 后续排序:访问结点的孩子,然后是该结点。
- 可能是点错了吧。····
- 错题2:The simulated link strategy does not allow array positions to be allocated contiguously regardless of the completeness of the tree.
A .True
B .False - 错题二理解情况:用数组模拟链表策略,可以连续分配数组位置。我以为考点是后面的完整性,没看到前面的不允许连续分配数组位置。
点评模板:
博客或代码中值得学习的或问题:
- 内容充实,课本知识讲解到位。
- 对于概念的不理解能够深究,提升自己。
- 但是参考资料那一块,有点敷衍。
本周结对学习情况
- [20172310](http://www.cnblogs.com/Qiuxia2017/)
- 结对学习内容
- 第十章:树
- 第七章:迭代器;
其他(感悟、思考等,可选)
这一章树对我来说是很难的,书上的很多代码都是看不懂的。经过问同学、查资料才明白了不少。还有就是迭代器那一章之前没有看,现在看了一下。这一周虽然很多作业、但是感觉很充实。
学习进度条(上学期截止7200)
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 260/0 | 1/1 | 05/05 | |
| 第二周 | 300/560 | 1/2 | 13/18 | |
| 第三周 | 212/772 | 1/4 | 21/39 | |
| 第四周 | 330/1112 | 2/7 | 21/60 | |
| 第五周 | 1321/2433 | 1/8 | 30/90 | |
| 第六周 | 1024/3457 | 1/9 | 20/110 |
参考资料
- 1.重温数据结构
- 2.深入理解迭代器是怎样访问元素的
- 3.markdown格式



