KMP字符串匹配算法
KMP字符串匹配算法
文/编辑
KMP完全匹配算法和 Levenshtein相似度匹配算法是模糊查找匹配字符串中最经典的算法,配合近期技术栏目关于算法的探讨,从网上摘取了一些简要的内容,加上自己的一些理解,向大家普及一些这方面的知识,希望能抛砖引玉。
l 算法简介:
kmp算法是一种改进的字符串匹配算法,由D.E.Knuth与V.R.Pratt和J.H.Morris同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。KMP算法的关键是根据给定的模式串W1,m,定义一个next函数。next函数包含了模式串本身局部匹配的信息。
l KMP算法和传统算法的匹配比较:
1. 传统算法:
传统匹配思想是,从目标串Target的第一个字符开始扫描,逐一与模式串的对应字符进行匹配,若该组字符匹配,则检测下一组字符,如遇失配,则退回到Target的第二个字符,重复上述步骤,直到整个Pattern在Target中找到匹配,或者已经扫描完整个目标串也没能够完成匹配为止。假设模式串Pattern长度为m,目标串Target长度为n,则每次比较最多需要花费O(m)的时间,算法的复杂度为O((n-m+1)*m)。这种算法没有利用匹配过的信息,每次都从头开始比较,速度很慢。
2. KMP算法:
在传统算法的基础上,当匹配失败后,并不简单地从目标串下一个字符开始新一轮的检测,而是依据在检测之前得到的有用信息,或者说模式串本身的特征信息,取得next函数跳转的位置,直接跳过不必要每次从头检测,从而达到一个较高的检测效率。
l 算法实例说明:
假设在串S=”abcabcabdabba”中查找T=” abcabd”
1. 传统算法:
先是比较S[0]和T[0]是否相等,然后比较S[1] 和T[1]是否相等…我们发现一直比较到S[5] 和T[5]才不等。如图:
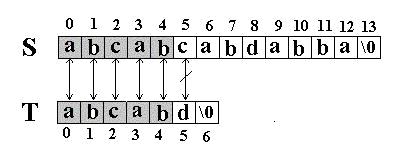
当这样一个失配发生时,T下标必须回溯到开始,S下标回溯的长度与T相同,然后S下标增1,然后再次比较。如图:
这次立刻发生了失配,T下标又回溯到开始,S下标增1,然后再次比较。如图:
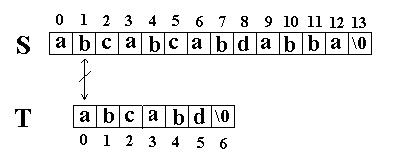
这次立刻发生了失配,T下标又回溯到开始,S下标增1,然后再次比较。如图:
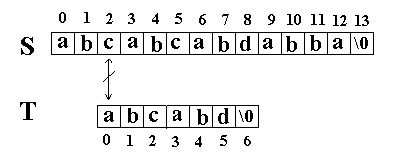
又一次发生了失配,所以T下标又回溯到开始,S下标增1,然后再次比较。这次T中的所有字符都和S中相应的字符匹配了。函数返回T在S中的起始下标3。如图:
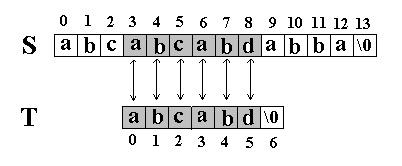
2. KMP算法:
还是相同的例子,在S=”abcabcabdabba”中查找T=”abcabd”,如果使用KMP匹配算法,当第一次搜索到S[5]和T[5]不等后,如图:

S下标不是回溯到1,T下标也不是回溯到开始,而是根据T中T[5]==’d’的模式函数值(next[5]=2),直接比较S[5] 和T[2]是否相等,因为相等,S和T的下标同时增加;因为又相等,S和T的下标又同时增加。。。最终在S中找到了T。如图:
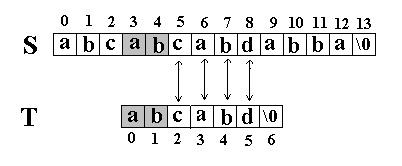
此处关键的问题是,为什么KMP算法能聪明的知道应该直接从S[5] 和T[2]开始比较呢?因为它能够利用已经得到的部分匹配信息来进行过滤。因为我们根据第一次比较得到的结果,如图:

很明显已经匹配了到了部分结果”abcab”,只是由于到T[5]==’d’的时候才无法和S[5]=’c’匹配上的,此时按传统算法T[0]应该重新开始和S[1]比较,但是根据之前的匹配结果S[1]等于T[1],但很明显T[0]不等于T[1],因此比较T[0]和S[1](也即T[1])是完全没有必要的。
以此类推,根据已经得到的结果”abcab”,T[0]重新开始比较的时候,应该和S[3](也即T[3])开始比较才是”明智”的。
因此 next[5]=2这个2表示T[5]==’d’的前面有2个字符和开始的两个字符相同,且T[5]==’d’不等于开始的两个字符之后的第三个字符(T[2]=’c’).如图:
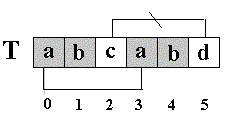
也就是说,如果开始的两个字符之后的第三个字符也为’d’,那么,尽管T[5]==’d’的前面有2个字符和开始的两个字符相同,T[5]==’d’的模式函数值也不为2,而是为0。
附件为KMP算法的实现java版,有兴趣的同事可以试试:
KMPMatchString.java



