POJ 1149 - PIGS - [最大流构图]
Time Limit: 1000MS Memory Limit: 10000K
Description
All data concerning customers planning to visit the farm on that particular day are available to Mirko early in the morning so that he can make a sales-plan in order to maximize the number of pigs sold.
More precisely, the procedure is as following: the customer arrives, opens all pig-houses to which he has the key, Mirko sells a certain number of pigs from all the unlocked pig-houses to him, and, if Mirko wants, he can redistribute the remaining pigs across the unlocked pig-houses.
An unlimited number of pigs can be placed in every pig-house.
Write a program that will find the maximum number of pigs that he can sell on that day.
Input
The next line contains M integeres, for each pig-house initial number of pigs. The number of pigs in each pig-house is greater or equal to 0 and less or equal to 1000.
The next N lines contains records about the customers in the following form ( record about the i-th customer is written in the (i+2)-th line):
A K1 K2 ... KA B It means that this customer has key to the pig-houses marked with the numbers K1, K2, ..., KA (sorted nondecreasingly ) and that he wants to buy B pigs. Numbers A and B can be equal to 0.
Output
Sample Input
3 3 3 1 10 2 1 2 2 2 1 3 3 1 2 6
Sample Output
7
从网上找了本宝典:[网络流建模汇总][Edelweiss].pdf,第一题就是这道题,看了之后那是恍然大悟,有一种醍醐灌顶的感觉,仿佛找寻到了最大流建图的入门诀窍
里面的描述是这样的:
华丽丽的分割线 begin
【题目大意】
有 M 个猪圈,每个猪圈里初始时有若干头猪。一开始所有猪圈都是关闭的。
依次来了 N 个顾客,每个顾客分别会打开指定的几个猪圈,从中买若干头猪。
每个顾客分别都有他能够买的数量的上限。每个顾客走后,他打开的那些猪圈中的猪,都可以被任意地调换到其它开着的猪圈里,然后所有猪圈重新关上。
问总共最多能卖出多少头猪。(1 <= N <= 100, 1 <= M <= 1000)
举个例子来说。有 3 个猪圈,初始时分别有 3、 1 和 10 头猪。
依次来了 3 个顾客,
第一个打开 1 号和 2 号猪圈,最多买 2 头;
第二个打开 1 号和 3 号猪圈,最多买 3 头;
第三个打开 2 号猪圈,最多买 6 头。
那么,最好的可能性之一就是第一个 顾客从 1 号圈买 2 头,然后把 1 号圈剩下的 1 头放到 2 号圈;
第二个顾客从 3 号圈买 3 头;
第三个顾客从 2 号圈买 2 头。
总共卖出 2+3+2=7 头。
【建模方法】 不难想象,这个问题的网络模型可以很直观地构造出来。就拿上面的例子来说, 可以构造出图 1 所示的模型(图中凡是没有标数字的边,容量都是∞):
• 三个顾客,就有三轮交易,每一轮分别都有 3 个猪圈和 1 个顾客的结点。
• 从源点到第一轮的各个猪圈各有一条边,容量就是各个猪圈里的猪的初始 数量。
• 从各个顾客到汇点各有一条边,容量就是各个顾客能买的数量上限。
• 在某一轮中,从该顾客打开的所有猪圈都有一条边连向该顾客,容量都是 ∞。
• 最后一轮除外,从每一轮的 i 号猪圈都有一条边连向下一轮的 i 号猪圈, 容量都是∞,表示这一轮剩下的猪可以留到下一轮。
• 最后一轮除外,从每一轮被打开的所有猪圈,到下一轮的同样这些猪圈, 两两之间都要连一条边,表示它们之间可以任意流通。
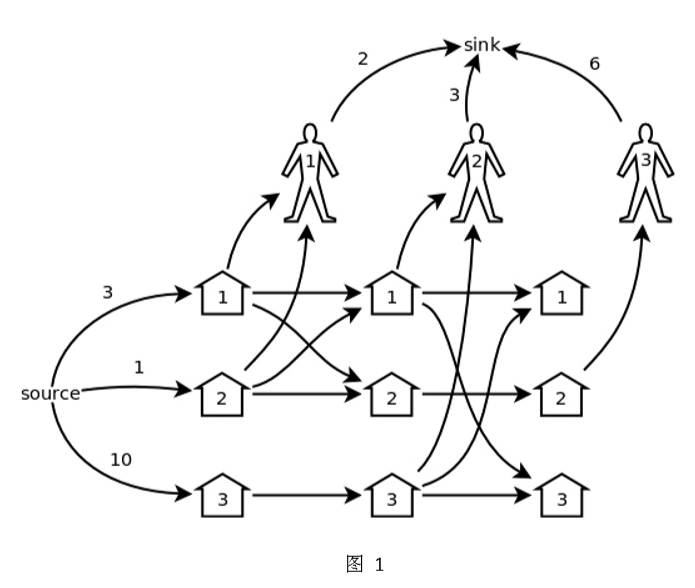
这个网络模型的最大流量就是最多能卖出的数量。图中最多有 2+N+M×N≈100,000 个结点。
这个模型虽然很直观,但是结点数太多了,计算速 度肯定会很慢。
其实不用再想别的算法,就让我们继续上面的例子,用合并的方 法来简化这个网络模型。
首先,最后一轮中没有打开的猪圈就可以从图中删掉了,也就是图 2 中红色 的部分,显然它们对整个网络的流量没有任何影响。
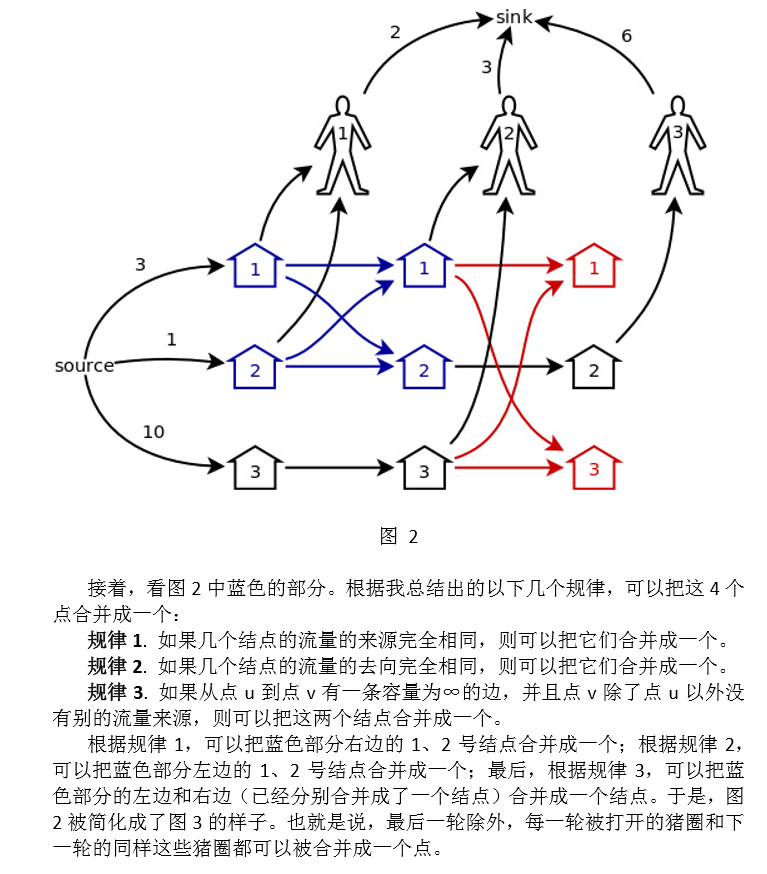
虽然我觉得他的思路非常的exciting,但是这里的三个简化规律我并不完全认同,网上也有一些人认为这三个规律有问题;就当他是对的吧,反正也想不出更好的简化办法……
但是我们先不管继续看下去:
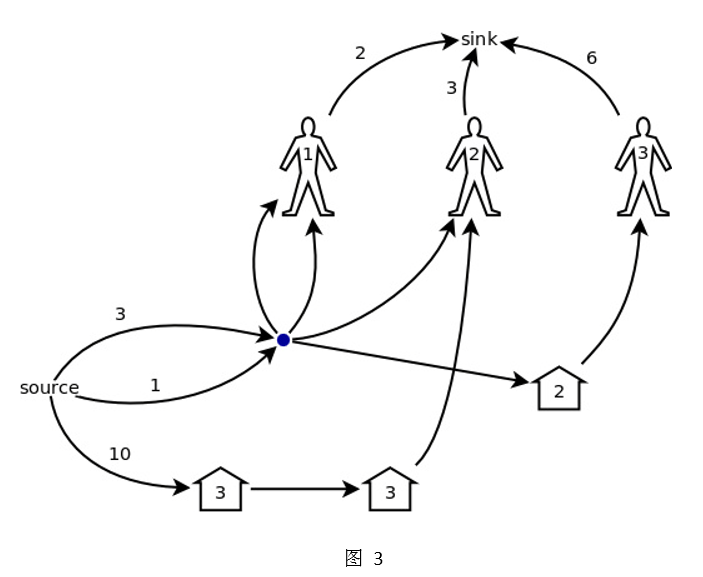
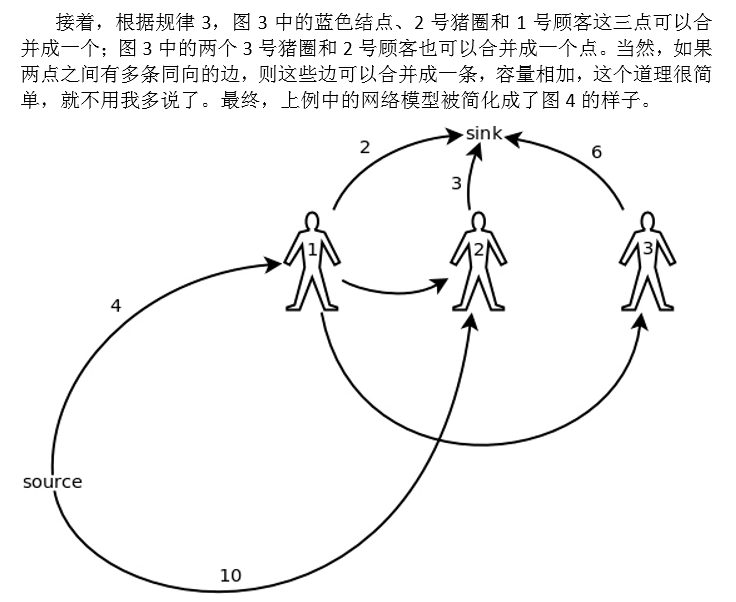
让我们从图 4 中重新总结一下构造这个网络模型的规则:
• 每个顾客分别用一个结点来表示。
• 对于每个猪圈的第一个顾客,从源点向他连一条边,容量就是该猪圈里的猪的初始数量。如果从源点到一名顾客有多条边,则可以把它们合并成一条,容量相加。
• 对于每个猪圈,假设有 n 个顾客打开过它,则对所有整数 i∈[1, n),从该 猪圈的第 i 个顾客向第 i + 1 个顾客连一条边,容量为∞。
• 从各个顾客到汇点各有一条边,容量是各个顾客能买的数量上限。
• 拿我们前面一直在讲的例子来说:
1 号猪圈的第一个顾客是 1 号顾客,所以 从源点到 1 号顾客有一条容量为 3 的边;
1 号猪圈的第二个顾客是 2 号顾客,因 此从 1 号顾客到 2 号顾客有一条容量为∞的边;
2 号猪圈的第一个顾客也是 1 号 顾客,所以从源点到 1 号顾客有一条容量为 1 的边,和之前已有的一条边合并起 来,容量变成 4;
2 号猪圈的第二个顾客是 3 号顾客,因此从 1 号顾客到 3 号顾 客有一条容量为∞的边;
3 号猪圈的第一个顾客是 2 号顾客,所以从源点到 2 号 顾客有一条容量为 10 的边。
新的网络模型中最多只有 2 + N = 102 个结点,计算速度就可以相当快了。
可以这样理解这个新的网络模型:
对于某一个顾客,如果他打开了猪圈 h,则在他走后,他打开的所有猪圈里剩下的猪都有可能被换到 h 中,因而这些猪都有可能被 h 的下一个顾客买走。
所以对于一个顾客打开的所有猪圈,从该顾客到各猪圈的下一个顾客,都要连一条容量为∞的边。
华丽丽的分割线 end
嗯,其实我觉得最后这两句话才是精髓,这是本题一个相当优秀的模型,简练而不失准确;
刚拿到题目可以想象,我们很一下子就想出这样的模型,但是通过对于一个原始而粗糙的模型的简化、归纳,进而寻找规律(尽管这一步中,可能会出现一些问题);
最后我们得到一个较为简洁明了的模型后,我们可以直接对这个模型进行验证,而不需要花大量时间在验证化简过程上。
在这样的模型指导下,代码就不是很难了……
(PS.由于Dinic算法对于重边的支持,所以我就没有像上面讲的那样,对重边进行合并……反正没几条边……我比较了一下合并和没合并的也没慢多少……)
1 #include<cstdio> 2 #include<cstdio> 3 #include<cstring> 4 #include<vector> 5 #include<queue> 6 #define MAXM 1003 7 #define MAXN 103 8 #define INF 0x3f3f3f3f 9 using namespace std; 10 struct Edge{ 11 int u,v,c,f; 12 }; 13 struct Dinic 14 { 15 int s,t; 16 vector<Edge> E; 17 vector<int> G[MAXN]; 18 bool vis[MAXN]; //BFS使用 19 int lev[MAXN];//记录层次 20 int cur[MAXN]; //当前弧下标 21 void addedge(int from,int to,int cap) 22 { 23 E.push_back((Edge){from,to,cap,0}); 24 E.push_back((Edge){to,from,0,0}); 25 int m=E.size(); 26 G[from].push_back(m-2); 27 G[to].push_back(m-1); 28 } 29 bool bfs() 30 { 31 memset(vis,0,sizeof(vis)); 32 queue<int> q; 33 q.push(s); 34 lev[s]=0; 35 vis[s]=1; 36 while(!q.empty()) 37 { 38 int now=q.front(); q.pop(); 39 for(int i=0;i<G[now].size();i++) 40 { 41 Edge edge=E[G[now][i]]; 42 int nex=edge.v; 43 if(!vis[nex] && edge.c>edge.f)//属于残存网络的边 44 { 45 lev[nex]=lev[now]+1; 46 q.push(nex); 47 vis[nex]=1; 48 } 49 } 50 } 51 return vis[t]; 52 } 53 int dfs(int now,int aug)//now表示当前结点,aug表示目前为止的最小残量 54 { 55 if(now==t || aug==0) return aug;//aug等于0时及时退出,此时相当于断路了 56 int flow=0,f; 57 for(int& i=cur[now];i<G[now].size();i++)//从上次考虑的弧开始,注意要使用引用,同时修改cur[now] 58 { 59 Edge& edge=E[G[now][i]]; 60 int nex=edge.v; 61 if(lev[now]+1 == lev[nex] && (f=dfs(nex,min(aug,edge.c-edge.f)))>0) 62 { 63 edge.f+=f; 64 E[G[now][i]^1].f-=f; 65 flow+=f; 66 aug-=f; 67 if(!aug) break;//aug等于0及时退出,当aug!=0,说明当前节点还存在另一个增广路分支 68 } 69 } 70 return flow; 71 } 72 int maxflow()//主过程 73 { 74 int flow=0; 75 while(bfs())//不停地用bfs构造分层网络,然后用dfs沿着阻塞流增广 76 { 77 memset(cur,0,sizeof(cur)); 78 flow+=dfs(s,INF); 79 } 80 return flow; 81 } 82 }dinic; 83 int m,n; 84 int pighouse[MAXM];//record the initial number of pigs in each pighouse 85 int vis[MAXM];//如果这个猪圈已经有了第一个顾客,就标记 86 int map[MAXN][MAXN]; 87 int main() 88 { 89 memset(vis,0,sizeof(vis)); 90 memset(map,0,sizeof(map)); 91 scanf("%d%d",&m,&n);//m pighouses, n customers 92 dinic.s=0, dinic.t=n+1; 93 for(int i=1;i<=m;i++) scanf("%d",&pighouse[i]); 94 for(int cus_id=1;cus_id<=n;cus_id++) 95 { 96 int A,B,num; 97 scanf("%d",&A); 98 for(int j=1;j<=A;j++) 99 { 100 scanf("%d",&num); 101 if(!vis[num])//cus_id号顾客是num号pighouse的第一个顾客 102 { 103 dinic.addedge(dinic.s,cus_id,pighouse[num]); 104 vis[num]=cus_id;//标记为customer的id,方便后面使用 105 } 106 else 107 { 108 dinic.addedge(vis[num],cus_id,INF); 109 vis[num]=cus_id; 110 } 111 } 112 scanf("%d",&B); 113 if(B==0) continue; 114 dinic.addedge(cus_id,dinic.t,B); 115 } 116 printf("%d\n",dinic.maxflow()); 117 }最大流的题,做起来真是让人心情愉悦呢
 妈个鸡如果不算把vis数组定义成bool类型然后WA5发的话,草草草……
妈个鸡如果不算把vis数组定义成bool类型然后WA5发的话,草草草……


