POJ1034 The dog task

题目来源：http://poj.org/problem?id=1034

题目大意：

　　一个猎人在遛狗。猎人的路径由一些给定的点指定。狗跟随着猎人，要与主人同时到达那些指定的点。在丛林里有一些有趣的地方，狗很喜欢去。狗在从一个指定点到达另一个指定点之间最多可以去访问一个有趣的地方。每个有趣的地方狗最多去访问一次。猎人总是匀速沿直线从一个点去往下一个点，狗的速度不超过猎人速度的两倍。（如下图，图中直线为猎人路线，虚线为狗的路径，黑点为有趣的地方。）

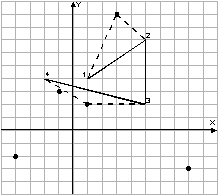
　　现给出猎人的路径，和所有有趣的点的坐标，求狗的路径，使得狗可以访问最多有趣的地方。

输入：第一行两个整数N（2<=N<=100）和M（0<=M<=100），N表示猎人的路径中指定的点数，M为有趣的地方的数目。第二行N对整数，指定猎人路径中指定点的坐标。第三行M对整数，指定有趣的地方的坐标。

输出：第一行输出一个整数K表明输出的狗的路径中顶点的个数。第三行K对整数表示狗的路径顶点坐标。

---

Sample Input

4 5
1 4 5 7 5 2 -2 4
-4 -2 3 9 1 2 -1 3 8 -3

Sample Output

6
1 4 3 9 5 7 5 2 1 2 -2 4

---

本题用到了很巧妙的建模方法，把问题转化为二部图的最大匹配问题，然后用经典的匈牙利算法解决。

　　二部图如下图所示：

　　图的顶点(这里称之为node)分为两个部分，图的边所连接的两个顶点均分别属于两个部分。

　　在我们的问题里，可以为每个猎人路径的相邻顶点(称之为vertex)之间的边建立一个node，把所有这些node的集合作为二部图的一边，所有有趣的地点作为二部图的另一部分的node。

　　node之间是否相连取决于狗在访问两个相邻vertex之间能否访问这个有趣的地方（有速度的约束，通过距离求解）。若可以访问，将对应的node连接起来。

　　建立起了二部图之后，就是要求解一个二部图的最大匹配了。匹配即图两部分顶点之间的配对，最大匹配即配对数对多的配对方式，显然求出最大匹配就解决了我们的问题。

　　有一种经典的匈牙利算法可以很简单的解决这个问题。依我的理解匈牙利算法应该用了贪心和dfs的思想。

　　首先，需要理解增广路的概念，下面用一个实例来解释。假设现有一个初始匹配（二部图中一些被选中的边的集合）：

   

   图1                     图2

如图1粗线所示。一条增广路就是：假设从左边的顶点开始查找，找到一个没有被匹配的点（3），从3出发找一条没有被选中的边（3-6），到达一个顶点6，发现6已经被匹配了，那么沿着与6匹配的边（6-2）到达2，再由2找一条不在匹配中的边（2-5）到达顶点5，5已被匹配，则继续沿匹配中的边（5-1）到达1，选与1相连但未在匹配中的边（1-4）找到4，此时顶点4无法再找到与之匹配的点，则一条增广路径(3->6->2->5->1->4)找到了。增广路的实质特点是：

　　1.路径段数一定是奇数，第一条边和最后一条边都没有被初始匹配选中。

　　2.路径中选中的边和未选中的边交替出现。

　　3.被选中的边数比未选中的边数多1。

基于上述三个特点，对于一个初始匹配，若能找到一条增广路径，只要把路径中选中的边从匹配中删除，把路径中未选中的边加入匹配，则匹配数增加了1.如果对于一个匹配无法再找到增广路，说明已经是最大匹配。

没明白的话看一下别人总结的“一句话”描述：“从二部图中找出一条路径来，让路径的起点和终点都是还没有匹配过的点，并且路径经过的连线是一条没被匹配、一条已经匹配过，再下一条又没匹配这样交替地出现。找到这样的路径后，路径里没被匹配的连线比已经匹配了的连线多一条，于是修改匹配图，把路径里所有匹配过的连线去掉匹配关系，把没有匹配的连线变成匹配的，这样匹配数就比原来多1个。不断执行上述操作，直到找不到这样的路径为止。”

个人认为找增广路的思想属于贪心的方法，而找增广路的过程是一个dfs的过程。

//////////////////////////////////////////////////////////////////////////
//        POJ1034 The dog task
//        Memory: 296K        Time: 47MS
//        Language: C++        Result: Accepted
//////////////////////////////////////////////////////////////////////////

#include <iostream>
#include <math.h>

using namespace std;

struct Point{
    int x;
    int y;
};
bool graph[101][101];
Point hunterRoute[101];
int hunterRouteCnt;
Point interestingPlaces[101];
int interestingPlacesCnt;
int link[101];
int ans[101];
int linkCnt;
bool visited[101];

void readData() {
    cin >> hunterRouteCnt >> interestingPlacesCnt;
    for (int i = 1; i <= hunterRouteCnt; ++i) {
        cin >> hunterRoute[i].x >> hunterRoute[i].y;
    }
    for (int i = 1; i <= interestingPlacesCnt; ++i) {
        cin >> interestingPlaces[i].x >> interestingPlaces[i].y;
    }
}

bool check (int x, int y) {
    double x1 = hunterRoute[x].x;
    double y1 = hunterRoute[x].y;
    double x2 = hunterRoute[x + 1].x;
    double y2 = hunterRoute[x + 1].y;
    double xd = interestingPlaces[y].x;
    double yd = interestingPlaces[y].y;
    double distance1 = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
    double distance2 = sqrt((x1 - xd) * (x1 - xd) + (y1 - yd) * (y1 - yd));
    double distance3 = sqrt((xd - x2) * (xd - x2) + (yd - y2) * (yd - y2));
    return distance2 + distance3 <= distance1 * 2 ? true : false;
}
void createGraph() {
    memset(graph, false, sizeof(graph));
    for (int i = 1; i < hunterRouteCnt; ++i) {
        for (int j = 1; j <= interestingPlacesCnt; ++j) {
            graph[i][j] = check(i, j);
        }
    }
}

bool dfs(int i) {
    for (int k = 1; k <= interestingPlacesCnt; ++k) {
        if (graph[i][k] == true && visited[k] == false) {
            visited[k] = true;
            if (link[k] == 0 || dfs(link[k])) {
                link[k] = i;
                ans[i] = k;
                return true;
            }
        }
    }
    return false;
}

void findMaxMatch() {
    memset(ans, 0, sizeof(ans));
    memset(link, 0, sizeof(link));
    linkCnt = 0;
    for (int i = 1; i < hunterRouteCnt; ++i) {
        memset(visited, false, sizeof(visited));
        if (dfs(i) == true) {
            ++linkCnt;
        }
    }
}

void output() {
    cout << linkCnt + hunterRouteCnt<<endl;
    for (int i = 1; i < hunterRouteCnt; ++i) {
        cout << hunterRoute[i].x << " " << hunterRoute[i].y << " ";
        if (ans[i] != 0) {
            cout << interestingPlaces[ans[i]].x << " " << interestingPlaces[ans[i]].y << " ";
        }
    }
    cout << hunterRoute[hunterRouteCnt].x << " " << hunterRoute[hunterRouteCnt].y;
}
int main() {
    while (cin >> hunterRouteCnt >> interestingPlacesCnt) {
        memset(graph,false,sizeof(graph));
        for (int i = 1; i <= hunterRouteCnt; ++i) {
            cin >> hunterRoute[i].x >> hunterRoute[i].y;
        }
        for (int i = 1; i <= interestingPlacesCnt; ++i) {
            cin >> interestingPlaces[i].x >> interestingPlaces[i].y;
        }
        createGraph();
        findMaxMatch();
        output();
    }
    system("pause");
    return 0;
}