PyTorch中的backward [转]

转自：https://sherlockliao.github.io/2017/07/10/backward/

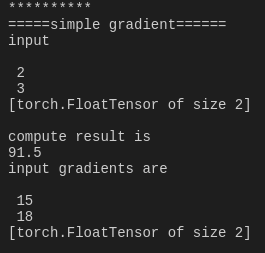
backward只能被应用在一个标量上，也就是一个一维tensor，或者传入跟变量相关的梯度。

特别注意Variable里面默认的参数requires_grad=False，所以这里我们要重新传入requires_grad=True让它成为一个叶子节点。

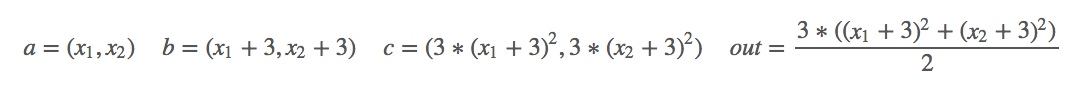
对其求偏导：

import torch as t
from torch.autograd import Variable as v

# simple gradient
a = v(t.FloatTensor([2, 3]), requires_grad=True)
b = a + 3
c = b * b * 3
out = c.mean()
out.backward()
print('*'*10)
print('=====simple gradient======')
print('input')
print(a.data)
print('compute result is')
print(out.data[0])
print('input gradients are')
print(a.grad.data)

 

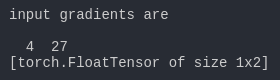
下面研究一下如何能够对非标量的情况下使用backward。backward里传入的参数是每次求导的一个系数。

首先定义好输入m=(x1,x2)=(2,3)，然后我们做的操作就是n=，这样我们就定义好了一个向量输出，结果第一项只和x1有关，结果第二项只和x2有关，那么求解这个梯度，

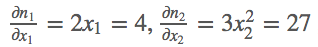
# backward on non-scalar output
m = v(t.FloatTensor([[2, 3]]), requires_grad=True)
n = v(t.zeros(1, 2))
n[0, 0] = m[0, 0] ** 2
n[0, 1] = m[0, 1] ** 3
n.backward(t.FloatTensor([[1, 1]]))
print('*'*10)
print('=====non scalar output======')
print('input')
print(m.data)
print('input gradients are')
print(m.grad.data)

 

jacobian矩阵

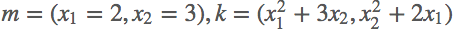
对其求导：

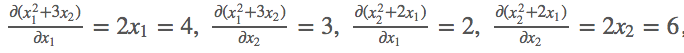
k.backward(parameters)接受的参数parameters必须要和k的大小一模一样，然后作为k的系数传回去，backward里传入的参数是每次求导的一个系数。

# jacobian
j = t.zeros(2 ,2)
k = v(t.zeros(1, 2))
m.grad.data.zero_()
k[0, 0] = m[0, 0] ** 2 + 3 * m[0 ,1]
k[0, 1] = m[0, 1] ** 2 + 2 * m[0, 0]
# [1, 0] dk0/dm0, dk1/dm0
k.backward(t.FloatTensor([[1, 0]]), retain_variables=True) # 需要两次反向求导
j[:, 0] = m.grad.data
m.grad.data.zero_()
# [0, 1] dk0/dm1, dk1/dm1
k.backward(t.FloatTensor([[0, 1]]))
j[:, 1] = m.grad.data
print('jacobian matrix is')
print(j)

我们要注意backward()里面另外的一个参数retain_variables=True，这个参数默认是False，也就是反向传播之后这个计算图的内存会被释放，这样就没办法进行第二次反向传播了，所以我们需要设置为True，因为这里我们需要进行两次反向传播求得jacobian矩阵。