省选算法学习-插头dp
插头dp?你说的是这个吗?

好吧显然不是......
所谓插头dp,实际上是“基于连通性的状态压缩dp”的简称,最先出现在cdq的论文里面
本篇博客致力于通过几道小小的例题(大部分都比较浅显)来介绍一下这种思路清奇的dp是怎么回事
Part I 定义
何为插头?
插头实际上是一个代称,代指两个格之间的连通性
若dp的某一个状态中,有某相邻的两个格子是联通的(比如说处在同一条路径上、被同一个矩形覆盖blablabla),我们就认为这两个格子之间有插头
举个栗子,格子(1,1)和格子(2,1)联通,那么格子(1,1)就有一个下插头,而格子(2,1)有一个上插头,如下图所示

每一个格子可以有的插头数量随着题目而变
对于一道用路径覆盖棋盘的题目(不相交不重叠的路径)而言,每个格子最多有两个插头:这种情况下表示有一条路径从这个格子的某一个插头的那个方向进来,又从另一个插头的那个方向出去了
例如一条回路的插头表示:
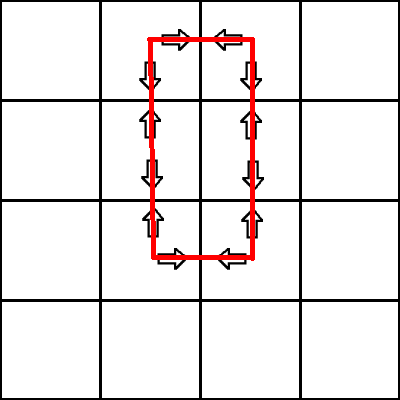
何为轮廓线?
轮廓线就是一条分割线,分隔了dp已经覆盖的状态和暂未覆盖的状态,它是在插头dp的棋盘模型中被定义的
插头dp有两种dp方式:逐行递推和逐格递推,其中逐行递推因为在很多题目中状态过多被弃用
当然也不是说逐行递推就没有用了, 但是本文主要讲逐格递推
逐格递推中,轮廓线是这样的:设当前正在递推的格子是(i,j)
那么轮廓线就是一条从棋盘左边界开始,沿着第i行的格子底部向右延伸至格子(i,j)的左下角,然后向上一格,再一直向右延伸到棋盘右边界
轮廓线的长度是m+1,其中m是列数
对于插头dp的棋盘模型,轮廓线上的不同插头状态就是dp的状态,因此可以引出插头dp棋盘模型的状态定义:
定义$dp\left[i\right]\left[j\right]\left[S\right]$表示如下条件时,插头dp的状态:
当前逐格递推到了第$i$行第$j$列的格子,轮廓线上方的插头状态为$S$,其中$S$的是状态压缩的
轮廓线的一个例子如下图:

其中黄色格子是当前正在递推(也就是正在从黄色格子左边的那个格子往黄色格子转移)的格子,红色的就是轮廓线
轮廓线的上方有m个下插头位置和一个右插头位置
PART II 棋盘模型
棋盘模型是插头dp的最常见(前几年最喜欢考)的方法
大概考法就是给你一个比较小的棋盘(15*15左右?或者更大一点),上面可能有些格子是障碍,然后让你用一些闭合路径啊,哈密顿回路啊或者一些奇奇怪怪的形状来覆盖棋盘上的每一个格子
还有一种考法就是给每个格子赋一个权值,然后让你找一条最优的回路或者路径或者某特定形状之类的
这一类题目有一个关键点:把轮廓线画出来以后,轮廓线上方的会是一些完备的“题目要求的形状”和一些“一头扎到”轮廓线下面,也就是被轮廓线切割的形状,而这些被切割的形状在轮廓线上方的分布我们不清楚,但是我们可以用轮廓线上插头的状态来表示所有情形的和
举个例子,现在有一条轮廓线,轮廓线上面有一些插头。我们现在可能不知道轮廓线上面的情况具体是怎么样的,但是我们根据这些插头就能往下推下面的状态
所以我们只要记录这种插头状态下轮廓线上方的答案,然后往下推就好了
也就是说我们把一个需要dfs找覆盖的问题转化成了一个dp模型~
现在的问题就是,我们怎么表示轮廓线上方的插头的状态呢?
cdq在论文中为我们提供了一个比较好的通解——最小表示法
最小表示法是这样的:对于一类插头可以互相配对的dp问题,我们有以下结论:
设从左到右的四个插头a,b,c,d,其中ac配对bd配对,而ab不配对:这种情况不可能存在
因此此时一定要么ab配对cd配对,要么ad配对bc配对
最小表示法,就是从左到右扫一遍所有插头,并这样操作:
如果这个插头已经被标记过了,就跳过
如果没有,设当前的插头是第i个未标记的插头
将所有当前插头联通的插头标记为i,然后进入下一个插头
这养的方法,由于插头dp本身是基于连通性的,所以一定可行,但是缺点是其时间效率可能较低
因此,对于每一道题,我们在确定最小表示法可以的前提下,可以再多加探索一些别的方法
比如下面这道例题:URAL1519
这道题利用的就是括号序列
又比如这道题:BZOJ2331
这道题利用L形自身的性质定义了插头(我甚至都不确定这道题最小表示法能不能用)
棋盘模型的例题很多,这里列举一些供大家参考
HNOI2004 邮递员
HDU1693 eat the trees
POJ1739 Tony's tour
ZJOI2009 多米诺骨牌 (这个准确来说不是插头dp,但是如果只有要求跨越每一行的话可以插头解决)
这些题目的写法基本都是大同小易,都是共同的,很多题甚至可以用同一份代码过掉
但是一定要多写,因为这样才能让插头dp真正熟记于心,同时处理不同的题目也能加深理解
PART III 直线模型
先鸽着......还没学透
例题:NOI2007生成树计数,GDKOI2018d1t4(大概?)
终于!终于!时隔八个月!博主终于打破了咕咕咕的记录!我把NOI2007生成树计数做了!
然后发现其实能讲的不多......
基础原理
我们知道,插头dp的本质,是“基于连通性的状态压缩dp”
那么对于一类构造图/回路/生成树的题目,我们就可以以对一部分点或者边的连通性的描述作为dp的状态,然后进行转移
举个栗子:NOI2007生成树计数
这道题目利用了给定的图的边的特性,推出了一个状态树比较少的dp,然后套进了矩阵快速幂里面做完。
注意这道题目同样利用了最小表示法,又根据第二类斯特林数的理论得到总的状态数很少
方法特性&&注意事项
这个模型的题目,代码复杂度和讨论复杂度和棋盘模型比起来会少很多,但是它的难点不在于这里
这个模型的难点在于构造出符合“无后效性”和“状态不重复不遗漏”的dp状态
同时,要注意到“轮廓线”的概念依然存在于直线模型中,只是它的存在被编辑成了其它的形式,例如上一道例题中的
最后,一定要熟记最小表示法的应用
PART IV 总结
插头dp平时可以见到的题目比较少,但是这并不妨碍插头dp成为众多优秀的dp模型中最具有思维复杂度以及讨论的美感的dp之一
考试中遇到插头dp的概率不大
如果遇到了棋盘模型请谨慎开题,避免全场刚一道导致爆炸;
如果遇到了直线模型,请......结合具体问题分析吧【因为实在是变数很多】
最后,不要学习我把一个知识点咕咕咕了长达八个月的时间>_<
 第四周总结 插头dp
第四周总结 插头dp

