[URAL1519] Formula 1 [插头dp入门]

题面：

传送门

思路：

插头dp基础教程

先理解一下题意：实际上就是要你求这个棋盘中的哈密顿回路个数，障碍不能走

看到这个数据范围，还有回路处理，就想到使用插头dp来做了

观察一下发现，这道题因为都是回路，所以联通块上方的插头一定两两配对，可以使用括号序列代替最小表示法

分情况讨论一下

情况一：当前格子上方和左方都没有插头

这种时候可以继续，也可以给当前格子加一个下插头一个右插头，相当于一个新的联通分量

 

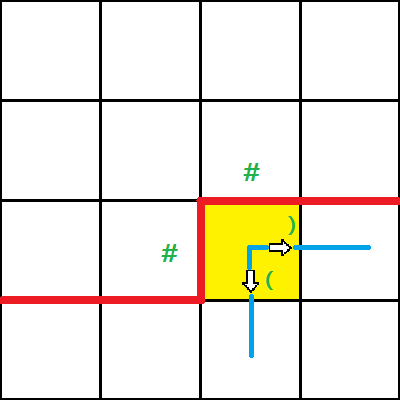
情况二：上方有一个下插头，左边没有

这时有两个决策：可以向右转，也可以继续向下，操作就是分别给这个格子一个右插头或者一个下插头

注意此时新插头的括号类型和原来的那个插头相同（画个图可以理解一下）

 

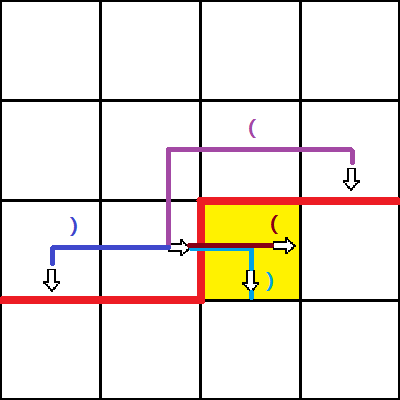
情况三：左边有一个右插头，上面没有

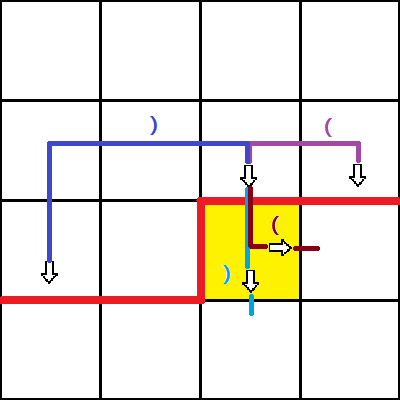
同情况二，转弯或者直走

 

 

情况四：都有插头，而且两个插头是同一括号

这种情况，我们可以将这两个插头合并，在当前格子把这条路径封闭了

但是这里需要考虑一下其他的插头

我们去掉了两个相同的括号，就需要把另外一个括号反过来配对才行

比如当前的括号序列是 ((##()#())##)，加粗的是我们要合并的两个括号，那么这两个)变成#以后，它们原来匹配的左括号(就失配了，需要其中一个（右边的那个）左括号变成右括号，两个重新配对

也就是((##()#())##)变成((##()#(####)变成((##()#)####)

当然也可以画个图理解一下，两条路径相当于是绕了圈接起来了

 

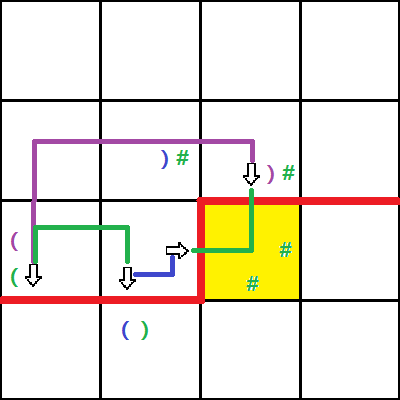
这个操作需要扫一遍整个序列，是$O\left(n\right)$的，当然也可以预处理变成$O\left(1\right)$

 

 

 

情况五：都有插头，且两个是)(

这时候直接合并就好了，图片同上（理解一下，博主懒得再画一个图了.......）

情况六：都有插头，而且两个是()

这种时候只有在最后一个非障碍格子才能合并，标志着路径完全封闭，得到了一个答案

 

 

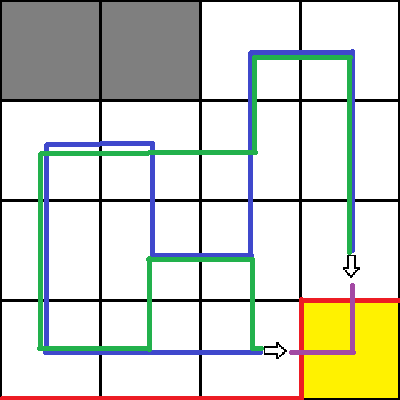
图中的蓝色和绿色代表样例中的两条路径，再最后一个格子合并

 

 

状态数略多，可以滚动数组+哈希处理

分类讨论的时候注意可不可以这么做（需要判断下一个格子是否为障碍）

 

Code：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #define ll long long
 6 #define hash ddf
 7 using namespace std;
 8 int n,m,x[15][15],cur,pre,ex,ey;
 9 int st[2][300010];ll ans[2][300010],re;
10 int tot[2],bit[20],state[300010],st_tot,hash=300000;
11 struct edge{
12     int to,next;
13 }a[300010];
14 void insert(int sta,ll val){
15 //    cout<<"insert "<<sta<<ends<<val<<endl;
16     int p=sta%hash,i;
17     for(i=state[p];i;i=a[i].next){
18         if(st[cur][a[i].to]==sta){
19             ans[cur][a[i].to]+=val;return;
20         }
21     }
22     tot[cur]++;
23     a[++st_tot].to=tot[cur];
24     a[st_tot].next=state[p];
25     state[p]=st_tot;st[cur][tot[cur]]=sta;ans[cur][tot[cur]]=val;
26 }
27 int main(){
28     int i,j,k,l,now,down,right;ll val;char s[20];
29     scanf("%d%d",&n,&m);
30     for(i=1;i<=n;i++){
31         scanf("%s",s);
32         for(j=0;j<m;j++) 
33             if(s[j]=='.') 
34                 x[i][j+1]=1,ex=i,ey=j+1;
35     }
36     for(i=1;i<15;i++) bit[i]=i<<1;
37     cur=0;tot[cur]=1;ans[cur][1]=1;st[cur][1]=0;
38     for(i=1;i<=n;i++){
39         for(j=1;j<=tot[cur];j++) st[cur][j]<<=2;
40         for(j=1;j<=m;j++){
41 //            cout<<"begin "<<i<<ends<<j<<endl;
42             st_tot=0;memset(state,0,sizeof(state));
43             pre=cur;cur^=1;tot[cur]=0;
44             for(k=1;k<=tot[pre];k++){
45                 now=st[pre][k];val=ans[pre][k];
46                 down=(now>>bit[j-1])%4;right=(now>>bit[j])%4;
47 //                cout<<"    from "<<now<<ends<<val<<ends<<down<<ends<<right<<endl;
48                 if(!x[i][j]){
49                     if(!down&&!right){
50                         insert(now,val);continue;
51                     }
52                 }
53                 else if(!down&&!right){
54                     if(x[i][j+1]&&x[i+1][j])
55                         insert(now+(1<<bit[j-1])+((1<<bit[j])<<1),val);
56                 }
57                 else if(!down&&right){
58                     if(x[i][j+1]) insert(now,val);
59                     if(x[i+1][j]) 
60                         insert(now-right*(1<<bit[j])+right*(1<<bit[j-1]),val);
61                 }
62                 else if(down&&!right){
63                     if(x[i+1][j]) insert(now,val);
64                     if(x[i][j+1])
65                         insert(now+down*(1<<bit[j])-down*(1<<bit[j-1]),val);
66                 }
67                 else if(down==1&&right==1){
68                     int cnt=1;
69                     for(l=j+1;l<=m;l++){
70                         if((now>>bit[l])%4==1) cnt++;
71                         if((now>>bit[l])%4==2) cnt--;
72                         if(!cnt){
73                             insert(now-(1<<bit[l])-(1<<bit[j])-(1<<bit[j-1]),val);
74                             break;
75                         }
76                     }
77                 }
78                 else if(down==2&&right==2){
79                     int cnt=1;
80                     for(l=j-2;l>=0;l--){
81                         if((now>>bit[l])%4==2) cnt++;
82                         if((now>>bit[l])%4==1) cnt--;
83                         if(!cnt){
84                             insert(now+(1<<bit[l])-((1<<bit[j])<<1)-((1<<bit[j-1])<<1),val);
85                             break;
86                         }
87                     }
88                 }
89                 else if(down==2&&right==1){
90                     insert(now-((1<<bit[j-1])<<1)-(1<<bit[j]),val);
91                 }
92                 else if(down==1&&right==2){
93                     if(i==ex&&j==ey) re+=val;
94                 }
95             }
96         }
97     }
98     printf("%lld\n",re);
99 }

 

posted @ 2018-03-21 09:29  dedicatus545  阅读(872)  评论(0)  编辑  收藏  举报