（原）使用mkl计算特征值和特征向量

转载请注明出处：

http://www.cnblogs.com/darkknightzh/p/5585271.html

参考文档：mkl官方文档

 

lapack_int LAPACKE_sgeev(int matrix_layout, char jobvl, char jobvr, lapack_int n, float* a, lapack_int lda, float* wr, float* wi, float* vl, lapack_int ldvl, float* vr, lapack_int ldvr);

说明：

用于计算n*n实/复非对称矩阵A的特征值和左/右特征向量。

A的右特征值v满足：A*v = λ*v，λ为特征值。

A的左特征值u满足：${{u}^{H}}*A=\lambda *{{u}^{H}}$，λ为特征值。 ${{u}^{H}}$为u的共轭转置。The computed eigenvectors are normalized to have Euclidean norm equal to 1 and largest component real。

输入：

matrix_layout：数据存储格式，行优先- LAPACK_ROW_MAJOR，列优先- LAPACK_COL_MAJOR

jobvl：‘N’，不计算A的左特征值；‘V’，计算A的左特征值。

jobvr：‘N’，不计算A的右特征值；‘V’，计算A的右特征值。

n：矩阵A的阶数(n≥ 0).

a：(大小最小 max(1, lda*n)) ，包含n*n 的矩阵 A.

lda：数组a的leading dimension. 最小max(1, n).

ldvl, ldvr：输出数组vl、vr的leading dimensions

    ldvl≥ 1; ldvr≥ 1.
    If jobvl = 'V', ldvl≥ max(1, n);
    If jobvr = 'V', ldvr≥ max(1, n).

输出：

a：该缓冲区会被覆盖

wr, wi：最小max (1, n) 的缓冲区。包含计算到的特征值的实部和虚部。

    Complex conjugate pairs of eigenvalues appear consecutively with the eigenvalue having positive imaginary part first.

vl, vr：

    vl (最小max(1, ldvl*n)) .

    jobvl = 'N'时，vl不使用

    计算到的特征值为实数时，对于第j个特征值：列优先时，第j个特征向量的第i个元素存储在vl[(i - 1) + (j - 1)*ldvl]（每行存储对应的特征向量）；行优先时，在vl[(i - 1)*ldvl + (j - 1)]（每列存储对应的特征向量）。

    计算到的特征值为复数及复矩阵的情况见官方文档。

    jobvr = 'N'时，不使用vr

    计算到的特征值为实数时，对于第j个特征值：列优先时，第j个特征向量的第i个元素存储在vr[(i - 1) + (j - 1)*ldvr]（每行存储对应的特征向量）；行优先时，在vr[(i - 1)*ldvr + (j - 1)]（每列存储对应的特征向量）。

    计算到的特征值为复数及复矩阵的情况见官方文档。

返回值：

0：计算成功

-i：第i个参数不合法

i：QR算法未能成功计算所有特征值，并且未计算任何特征向量。elements i+1:n of wr and wi (for real flavors) or w (for complex flavors) contain those eigenvalues which have converged.

 

lapack_int LAPACKE_ssyevd(int matrix_layout, char jobz, char uplo, lapack_int n, float* a, lapack_int lda, float* w);

说明：

计算实对称矩阵A所有特征值，（特征向量可选）。只计算特征值时，使用Pal-Walker-Kahan variant of the QL or QR算法。需要计算特征向量时，使用divide and conquer算法。

注意：

对于实对称问题，大部分情况下，默认的选择是syevr函数，该函数更快，并且内存使用更少。syevd函数需要更多内存，但是更快，特别是对于大矩阵。

输入：

matrix_layout：数据存储格式，行优先- LAPACK_ROW_MAJOR，列优先- LAPACK_COL_MAJOR

jobz：‘N’，只计算特征值；‘V’，计算特征值和特征向量。

uplo：‘U’，a存储了A的上三角部分；‘L’，a存储了A的下三角部分。

n：矩阵A的阶数(n≥ 0).

a：(大小max(1, lda*n)) ，包含实对称矩阵 A的上三角或下三角部分。通过参数uplo指定。

lda：数组a的leading dimension。最小max(1, n).

ldvl, ldvr：输出数组vl、vr的leading dimensions

    ldvl≥ 1; ldvr≥ 1.
    If jobvl = 'V', ldvl≥ max(1, n);
    If jobvr = 'V', ldvr≥ max(1, n).

输出：

w：数组，至少max(1, n)。当返回值为0时，包含升序的特征值。

a：当jobz = 'V'时，该参数会被正交的特征向量覆盖。

返回值：

0：计算成功

-i：第i个参数不合法

i：jobz = 'N'时，算法未能收敛；i indicates the number of off-diagonal elements of an intermediate tridiagonal form which did not converge to zero；

    jobz = 'V'时，the algorithm failed to compute an eigenvalue while working on the submatrix lying in rows and columns info/(n+1) through mod(info,n+1).

 

https://software.intel.com/en-us/articles/intel-mkl-111-release-notes

中写道：If LAPACKE_ssyevd fails to evaluate a matrix , workaround is to use LAPACKE_ssyev

lapack_int LAPACKE_ssyev(int matrix_layout, char jobz, char uplo, lapack_int n, float* a, lapack_int lda, float* w);

说明：

计算实对称矩阵A所有特征值，（特征向量可选）。

注意：

对于实对称问题，大部分情况下，默认的选择是syevr函数，该函数更快，并且内存使用更少。syevd函数需要更多内存，但是更快，特别是对于大矩阵。

输入：

matrix_layout：数据存储格式，行优先- LAPACK_ROW_MAJOR，列优先- LAPACK_COL_MAJOR

jobz：‘N’，只计算特征值；‘V’，计算特征值和特征向量。

uplo：‘U’，a存储了A的上三角部分；‘L’，a存储了A的下三角部分。

n：矩阵A的阶数(n≥ 0).

a：(大小max(1, lda*n)) ，包含实对称矩阵 A的上三角或下三角部分。通过参数uplo指定。

lda：数组a的leading dimension。最小max(1, n).

输出：

w：数组，至少max(1, n)。当返回值为0时，包含升序的特征值。

a：当jobz = 'V'时，如果info = 0，a中包含正交的特征向量。当jobz = 'N'时，包含对角线的下三角(uplo = 'L')或上三角(uplo = 'U')元素会被覆盖。

返回值：

0：计算成功

-i：第i个参数不合法

i：算法未能收敛。i indicates the number of elements of an intermediate tridiagonal form which did not converge to zero.

 

lapack_int LAPACKE_ssyevr(int matrix_layout, char jobz, char range, char uplo, lapack_int n, float* a, lapack_int lda, float vl, float vu, lapack_int il, lapack_int iu, float abstol, lapack_int* m, float* w, float* z, lapack_int ldz, lapack_int* isuppz);

说明：

计算实对称矩阵A所有特征值，（特征向量可选）。

可通过设定特征值的范围或者特征值的位置来选定特征值（Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.）

输入：

matrix_layout：数据存储格式，行优先- LAPACK_ROW_MAJOR，列优先- LAPACK_COL_MAJOR

jobz：‘N’，只计算特征值；‘V’，计算特征值和特征向量。

range：'A'，计算所有特征值；'V'，计算vl < w[i]≤vu在半开区间的特征值；'I'，计算索引从il到iu之内的特征值。

uplo：‘U’，a存储了A的上三角部分；‘L’，a存储了A的下三角部分。

n：矩阵A的阶数(n≥ 0).

a：(大小max(1, lda*n)) ，包含实对称矩阵 A的上三角或下三角部分。通过参数uplo指定。

lda：数组a的leading dimension。最小max(1, n).

vl, vu：range = 'V'时，计算到的特征值的左右边界（vl< vu）；range = 'A'或'I'，这两个参数不使用。

il, iu：当range = 'I'时，最小和最大特征值的索引。

    n > 0时，1 ≤il≤iu≤n

    n = 0时，il=1，iu=0

    range = 'A'或'V'时，不使用这两个参数。

abstol：当jobz = 'V'时，the eigenvalues and eigenvectors output have residual norms bounded by abstol, and the dot products between different eigenvectors are bounded by abstol.

    If abstol < n *eps*||T||, then n *eps*||T|| is used instead, where eps is the machine precision, and ||T|| is the 1-norm of the matrix T. The eigenvalues are computed to an accuracy of eps*||T|| irrespective of abstol.

ldz：输出缓冲区z的leading dimension。jobz = 'N'时，ldz≥ 1；jobz = 'V'时，列优先，ldz≥ max(1, n)；行优先，ldz≥ max(1, m)

输出：

a：包含对角线的下三角(uplo = 'L')或上三角(uplo = 'U')元素会被覆盖。

m：总共找到的特征值数量，0 ≤m≤n。range = 'A'时，m = n；range = 'I'时，m = iu-il+1；range ='V'时，m未知（the exact value of m is not known in advance）

w：数组，至少max(1, n)。，包含升序的特征值，存储在w[0]w[m - 1]。

z：列优先时，大小max(1, ldz*m)；行优先时，大小max(1, ldz*n)。jobz = 'V'时，如果返回值为0，z的前m列包含对应于特征值的正交的特征向量（with the i-th column of z holding the eigenvector associated with w[i - 1]）；jobz = 'N'时，不使用z。

isuppz：数组，最小 2 *max(1, m)。The support of the eigenvectors in z, i.e., the indices indicating the nonzero elements in z. The i-th eigenvector is nonzero only in elements isuppz[2i - 2] through isuppz[2i - 1]. Referenced only if eigenvectors are needed (jobz = 'V') and all eigenvalues are needed, that is, range = 'A' or range = 'I' and il = 1 and iu = n.

返回值：

0：计算成功

-i：第i个参数不合法

i：发生了内部错误。

 

程序：

下面的程序将参数固定了，实际上可自行调整。

// 计算矩阵的特征值和特征向量
int SEigen(float* pEigVal, float* pEigVec, const float* pSrc, int dim)
{
    float* eigValImag = new float[dim];
    float* eigVecVl = new float[dim * dim];
    float* pSrcBak = new float[dim * dim];
    memcpy(pSrcBak, pSrc, sizeof(float) * dim * dim);

    int nRetVal = LAPACKE_sgeev(LAPACK_ROW_MAJOR, 'N', 'V', dim, pSrcBak, dim,
        pEigVal, eigValImag, eigVecVl, dim, pEigVec, dim);   // 计算特征值和特征向量

    delete[] eigValImag;
    eigValImag = nullptr;
    delete[] eigVecVl;
    eigVecVl = nullptr;
    delete[] pSrcBak;
    pSrcBak = nullptr;

    return nRetVal;
}

// 计算实对称矩阵的特征值和特征向量
int SRealSymEigen1(float* pEigVal, float* pEigVec, const float* pSrc, int dim)
{
    memcpy(pEigVec, pSrc, sizeof(float)* dim * dim);
    return LAPACKE_ssyevd(LAPACK_ROW_MAJOR, 'V', 'U', dim, pEigVec, dim, pEigVal);   // 计算特征值和特征向量
}

// 计算实对称矩阵的特征值和特征向量
int SRealSymEigen2(float* pEigVal, float* pEigVec, const float* pSrc, int dim)
{
    memcpy(pEigVec, pSrc, sizeof(float)* dim * dim);
    return LAPACKE_ssyev(LAPACK_ROW_MAJOR, 'V', 'U', dim, pEigVec, dim, pEigVal);  // 计算特征值和特征向量
}

 

测试程序：

    const int nDim = 3;
    float pa[nDim * nDim] = { 1, 2, 3, 6, 5, 4, 7, 5, 8 };
    float eigVal[nDim];
    float eigVec[nDim * nDim];

    memset(eigVal, 0, sizeof(float)* nDim);
    memset(eigVec, 0, sizeof(float)* nDim * nDim);
    int ret1 = SEigen(eigVal, eigVec, pa, nDim);  // 计算非对称矩阵的特征值和特征向量

    memset(eigVal, 0, sizeof(float)* nDim);
    memset(eigVec, 0, sizeof(float)* nDim * nDim);
    int ret2 = SRealSymEigen1(eigVal, eigVec, pa, nDim);  // 计算实对称矩阵的特征值和特征向量

    int ret3 = SRealSymEigen2(eigVal, eigVec, pa, nDim);  // 计算实对称矩阵的特征值和特征向量

 

SRealSymEigen1中LAPACKE_sgeev结果：

特征值：

特征向量：

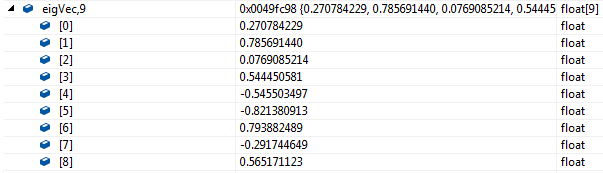
matlab结果：

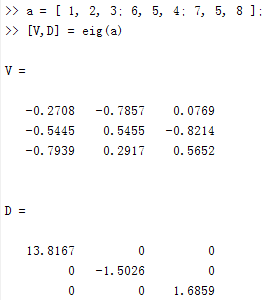
注意的是，C++中每列存储对应的特征向量。除了正负号之外，和matlab结果一致。

 

SrealSymEigen2中LAPACKE_ssyevd结果：

特征值：

特征向量：

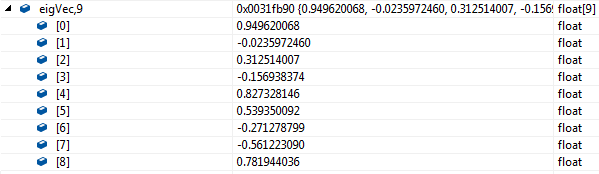
matlab结果：

可见结果一致。

注意：测试程序中，pa并不是对称矩阵，但是使用SRealSymEigen1后，仍旧能得到正确的结果。说明，LAPACKE_ssyevd不会校验输入矩阵是否对称，直接按照输入要求，把对应的上三角或下三角作为A矩阵进行计算。

 

SrealSymEigen3中LAPACKE_ssyev结果：

特征值：

特征向量：

可见和LAPACKE_ssyevd特征值一样，特征向量在误差允许的范围内一致。

 

对于最后一个函数LAPACKE_ssyevr：

// 计算实对称矩阵的特征值和特征向量
int SRealSymEigen3()
{
    const int nDim = 3;
    float a[nDim * nDim] = { 1, 2, 3, 6, 5, 4, 7, 5, 8 };
    float eigVal[nDim];
    float eigVec[nDim * nDim];
    int isuppz[nDim * 2] = { 0 };
    int m = 0;

    float aBakUp[nDim * nDim];
    memcpy(aBakUp, a, sizeof(float) * nDim * nDim);

    memset(eigVal, 0, sizeof(float)* nDim);
    memset(eigVec, 0, sizeof(float)* nDim * nDim);
    LAPACKE_ssyevr(LAPACK_ROW_MAJOR, 'V', 'A', 'U', nDim, aBakUp,
        nDim, -2, 5, 2, 3, 10, &m, eigVal, eigVec, nDim, isuppz);  // step1

    memcpy(aBakUp, a, sizeof(float)* nDim * nDim);
    memset(eigVal, 0, sizeof(float)* nDim);
    memset(eigVec, 0, sizeof(float)* nDim * nDim);
    LAPACKE_ssyevr(LAPACK_ROW_MAJOR, 'V', 'V', 'U', nDim, aBakUp,
         nDim, -2, 5, 2, 3, 10, &m, eigVal, eigVec, nDim, isuppz); // step2

    memcpy(aBakUp, a, sizeof(float)* nDim * nDim);
    memset(eigVal, 0, sizeof(float)* nDim);
    memset(eigVec, 0, sizeof(float)* nDim * nDim);
    LAPACKE_ssyevr(LAPACK_ROW_MAJOR, 'V', 'I', 'U', nDim, aBakUp,
         nDim, -2, 5, 2, 3, 10, &m, eigVal, eigVec, nDim, isuppz); // step3

     return 0;
}

执行完step1后：

特征值：

特征向量：

此时，所有特征值和特征向量都计算。

 

执行完step2后：

特征值：

特征向量：

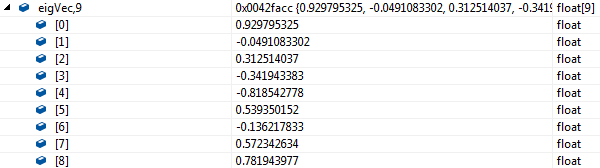
此时，只筛选了符合要求的特征值（特征向量全部保存），但是特征值也不完全对应，不懂。

 

执行完step3后：

特征值：

特征向量：

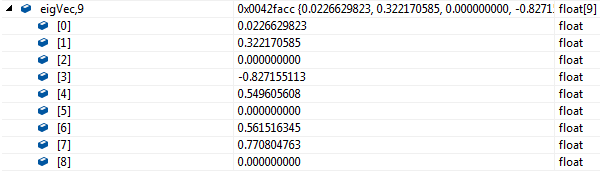
此时，特征值和特征向量都不对应，更不懂了。。。