（原）使用mkl中函数LAPACKE_sgesv计算矩阵的逆矩阵

转载请注明出处：

http://www.cnblogs.com/darkknightzh/p/5578027.html

参考文档：mkl的说明文档

 

lapack_int LAPACKE_sgesv(int matrix_layout, lapack_int n, lapack_int nrhs, float * a, lapack_int lda, lapack_int * ipiv, float * b, lapack_int ldb);

该函数计算AX=B的解。简单来说，当B为单位矩阵时，X即为inv(A)。

输入：

matrix_layout：矩阵存储顺序，C++中为行优先LAPACK_ROW_MAJOR

n：线性方程的个数，$n\ge 0$

nrhs：矩阵B的列数，$nrhs\ge 0$

a：大小max(1, lda*n)，包含n*n的系数矩阵A

b：列优先存储时，大小max(1, ldb* nrhs)；行优先存储时，大小max(1, ldb*n)；包含n* nrhs的矩阵B

lda：矩阵a的leading dimension，$lda\ge \max (1,n)$

ldb：矩阵b的leading dimension；列优先存储时，$ldb\ge \max (1,n)$；行优先存储时，$ldb\ge \max (1,nrhs)$

输出：

a：（具体看说明文档）可能会被覆盖

b：（具体看说明文档）调用此函数时被覆盖

ippv：（具体看说明文档）大小最小是max(1, n)

返回值：0成功，其他不成功

This function returns a value info.

If info=0, the execution is successful.

If info = -i, parameter i had an illegal value.

If info = i, ${{U}_{i,i}}$ (computed in double precision for mixed precision subroutines) is exactly zero. The factorization has been completed, but the factor U is exactly singular, so the solution could not be computed.

 

程序：

int SCalcInverseMatrix(float* pDst, const float* pSrc, int dim)
{
    int nRetVal = 0;
    if (pSrc == pDst)
    {
        return -1;
    }

    int* ipiv = new int[dim * dim];
    float* pSrcBak = new float[dim * dim];  // LAPACKE_sgesv会覆盖A矩阵，因而将pSrc备份
    memcpy(pSrcBak, pSrc, sizeof(float)* dim * dim);

    memset(pDst, 0, sizeof(float)* dim * dim);
    for (int i = 0; i < dim; ++i)
    {
        // LAPACKE_sgesv函数计算AX=B，当B为单位矩阵时，X为inv(A)
        pDst[i*(dim + 1)] = 1.0f;
    }

    // 调用LAPACKE_sgesv后，会将inv(A)覆盖到X（即pDst）中
    nRetVal = LAPACKE_sgesv(LAPACK_ROW_MAJOR, dim, dim, pSrcBak, dim, ipiv, pDst, dim);

    delete[] ipiv;
    ipiv = nullptr;

    delete[] pSrcBak;
    pSrcBak = nullptr;

    return nRetVal;
}

调用：

    const int nDim = 3;
    float pa[nDim * nDim] = { 1, 2, 3, 6, 5, 4, 7 ,5 ,8 };
    float pb[nDim * nDim];

    int nRetVal = SCalcInverseMatrix(pb, pa, nDim);

结果：

matlab调用inv后的结果：

 

可见在精度允许的范围内，结果一致。

 

另一方面，在调用LAPACKE_sgesv之前：

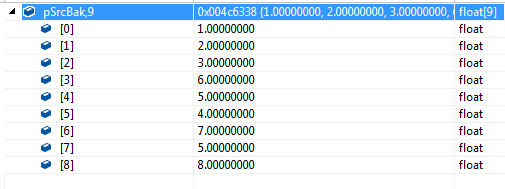
调用LAPACKE_sgesv之后：

可见，存储A的缓冲区被覆盖。