《编程珠玑，字字珠玑》1234读书笔记——多路归并排序

写在前面的

2012年3月25日买下《编程珠玑》，很期待但不知道它能给我带来什么！
编程珠玑，字字珠玑。但是翻译有点拗口，有时候整句话读下来都不知道在讲什么，多少有点掩饰了珠玑的魅力，真怀疑是不是直接有道翻译了。

位图数据结构法

在“开篇”的里，讲述了排序的一个问题，大意就是，对一个“最多占n位的（就是n位的整数），随机的，无重复的（互异无序）”的整数序列进行排序，那么这个序列的总长度len<=10^n。例如：这个序列中的每个整数最多占3位，那么序列最多有0~999的1000个数。

无重复会有很大的启发，可以试着使用“位图数据结构”来解决。位图数据结构？位图中的每个像素都被存储在计算机当中，并用一定的字节数来标记它的属性值。启发：如果是黑白的位图，那么位图中的每一个像素都可以用一个bool值来标记，因为位图无非就是黑与白，同理，可以应用到这个问题当中。

如果出现了，就用‘1’来标记；反之，用‘0’来标记，而用一个数组来表示给出的序列，那么数组的下标就是对应的出现的整数了。例如：dl[1]=1，那么，1在这个序列中有出现。这就是在统计出现与否的同时达到了排序了效果，而且节省了大量的时间与空间。这个效果与用排序模板和经常使用的外部（归并）排序比起来是绝对胜出的。

这是它“神奇”的地方，输入序列和输出序列都只有一次。1kw个上述整数序列也只用到了大约1.25M的内存空间。只能说，“位图数据结构法”在解决这样的问题有优势，只要把条件做小小的改动，情况会变得非常糟糕：把“互异”改为“非互异”，“位图法”无法胜任，还是要回到原始的外部排序算法。居然这样，那就一窥芳容。

多路归并排序 

外部排序，也就是借助了磁盘，所有的排序过程并不是都在内存中完成。所以，外部排序没什么可怕的，常用的外部排序就是多路归并排序，它归并排序是一样的。关于多路归并排序，在多路归并排序这篇博文当中写得很清楚，不罗嗦了，这篇博文写的很认真，这篇博文当是自己的学习笔记。

珠玑“开篇”的课后习题第3题所要解决的就是测试多路归并排序的首要问题，所以没了它，也是无米之炊。产生随机数可以用rand库函数，但是它有缺陷的，rand函数产生的随机数最大是32767，但是这里需要KW，甚至更大的数据。 
解决方法原理：可以依据“洗牌原理”，一副牌，将其中一张（任意挑选）与另一张（任意挑选）置换，...如此重复n次。牌没有增减，但是顺序打乱。

于是有下面的random代码：（不给出核心代码了，故意省略的，有心的根据上面的原理写出来，“原理”写的很清楚，借助rand库函数，还犹豫什么，快点写出来吧）

 

//range：范围 
//num：个数 
void random(int range,int num) 
{ 
    int * a = new int[range],i,j;
    srand(unsigned(time(NULL)));
    for(i=0; i<range; i++) 
        a[i] = i + 1;
    ....核心代码去哪里啦！
    //    写入文件 
    for(i=0; i<num; i++) 
        cout << a[i] << " ";
    //    回收 
    delete [] a; 
}

 

 

有了上面的基础，操刀就容易了。有下面的图，多路归并也就浮出水面！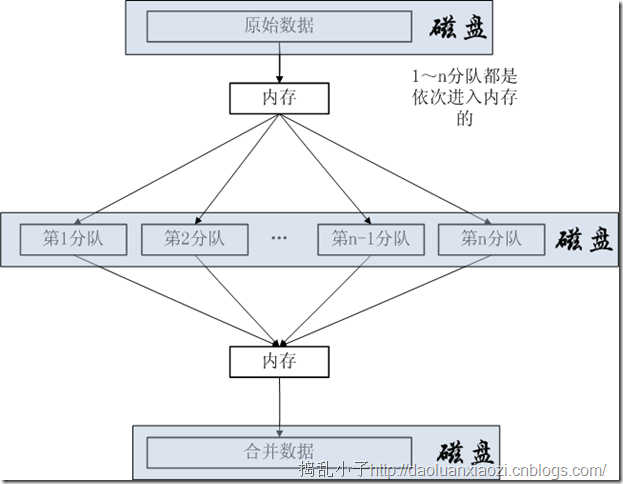
 

其实，数据结构课程中的归并排序就把原始数据分成了2个分队（二路），并且它的所有工作只在内存中完成，不借助磁盘，另外二路更多采用递归算法的。上图举例：1kw的个整数，每个整数4B，规定内存只有1M，那么每次读入内存(1MB/4B)=250k个整数，所以有(1kw/250k=40)个分队，下面称为“段文件”。

 

多路归并排序编程实现细节

• 内存排序环节：磁盘中的数据序列被分割成多个段（假定内存有限）读入到内存中，在内存中用模板sort实现排序过程，效率高！ 
• 多路归并排序环节：依次从从每个已排序的段文件中（什么是段文件，看上面的内存排序环节，形象了点！！）读入一个数据，注意是一个；挑选最小的写入的目标文件中。

 

数据的准备上面的random函数可以完全可以胜任。我测试的时候只准备了只有100w的数据，已经通过测试；小数据也可以通过，只是时间上有差异。

 

下面是代码（不怎么喜欢贴代码的，折叠起来）

#include <iostream>
#include <string.h>
#include <fstream>
#include <Algorithm>
#include <time.h>
using namespace std;

#define MAX 10000                //    总数据量，可修改
#define MAX_ONCE 2500        //    内存排序MAX_ONCE个数据
#define FILENAME_LEN 20    

//range：范围
//num：个数
void random(int range,int num)
{
    int * a = new int[range],i,j;
    fstream dist_file;

    srand(unsigned(time(NULL)));

    for(i=0; i<range; i++)
        a[i] = i + 1;

    //    打表预处理
    for(j=0; j<range; j++)
    {
        //    rand函数产生的随机数最大是32767，不能直接调用rand，做一下处理
        int ii = (rand()*RAND_MAX+rand()) % range,        
            jj = (rand()*RAND_MAX+rand()) % range;
        swap(a[ii],a[jj]);
    }// for

    dist_file.open("data.txt",ios::out);

    //    写入文件
    for(i=0; i<num; i++)
        dist_file << a[i] << " ";

    //    回收
    delete [] a;
    dist_file.close();
}

bool cmp(int &a,int &b)
{return a<b;}

//index：文件的下标
char * create_filename(int index)
{
    char * a = new char[FILENAME_LEN];
    sprintf(a,"data %d.txt",index);
    return a;
}

//num：每次读入内存的数据量
void mem_sort(int num)
{
    fstream fs("data.txt",ios::in);
    int temp[MAX_ONCE],    //    内存数据暂存
        file_index = 0,            //    文件下标
        i,
        cnt;                            //    实际读入内存数据量

    bool eof_flag = false;    //    文件末尾标识

    while(!fs.eof())
    {
        for(i=0,cnt = 0; i<MAX_ONCE; i++)
        {
            fs >> temp[cnt];

            //    读入一个数据后进行判断是否到了末尾
            if(fs.peek()==EOF)    
            {
                eof_flag = true;
                break;
            }// if

            cnt++;
        }// for

        if(eof_flag)
            break;

        //    内存排序
        sort(temp,temp+cnt,cmp);

        char * filename = create_filename(++file_index);
        fstream fs_temp(filename,ios::out);

        //    写入
        for(i=0; i<cnt; i++)
            fs_temp << temp[i] << " ";

        fs_temp.close();
        delete [] filename;
    }// while

    fs.close();
}

void merge_sort(int filecnt)
{
    fstream * fs = new fstream[filecnt],ret("ret.txt",ios::out);
    int index = 1,temp[MAX_ONCE],eofcnt = 0;
    bool * eof_flag = new bool[filecnt];

    ::memset(eof_flag,false,filecnt*sizeof(bool));

    for(int i=0; i<filecnt; i++)
        fs[i].open(create_filename(index++),ios::in);

    for(int i=0; i<filecnt; i++)
        fs[i] >> temp[i];

    while(eofcnt<filecnt)
    {    
        int j = 0;
        //    找到第一个未结束处理的文件
        while(eof_flag[j])
            j++;

        int min = temp[j],fileindex = 0;
        for(int i=j+1; i<filecnt; i++)
        {
            if(temp[i]<min && !eof_flag[i])
                min = temp[i],fileindex = i;
        }// for

        ret << min << " ";
        fs[fileindex] >> temp[fileindex];
        //    末尾判断
        if(fs[fileindex].peek()==EOF)
            eof_flag[fileindex] = true,
            eofcnt++;
    }// while

    delete [] fs;
    delete [] eof_flag;
    ret.close();
}

int main()
{
    random(MAX,MAX);
    clock_t begin = clock();
    mem_sort(MAX);
    merge_sort(4);
    clock_t end = clock();

    double cost = (end - begin)*1.0 / CLK_TCK;
    cout << "耗时：" << cost << "ms" << endl;
}

我的实现过程小瓶颈 

在用到c++的输入输出的流要特别注意，特别是输入流，因为在内存排序环节和多路归并排序环节都有涉及文件的读入，分别是从源文件中读入原始数据和从段文件中读入数据。在这个实验中，如果一时没处理好文件末尾的判断，会出现小小的瑕疵（在合并文件的末尾会出现数据丢失或者重复）。
根据经验最好的解决方法：每次处理文件数据之前，先读入一个数据之后，进行下面的判断，如果符合这个判断就表示要结束接下来的处理。因为即使刚好到了文件末尾，输入流也需要一个输入的牺牲来判断是否到了文件末尾，如果到了文件末尾，设置EOF标志。

 

if(fs.peek()==EOF)
{
    ...
    break;
}// if

 

只要依准这一原则，问题可以得到解决。

 

问题分析，数据结构选择，算法，和技巧 

1234章涉及了上面的话题，它决不能马上让你都有提高，重要的要在自己的学习中多加留意。比如第一章就提到的排序问题。想必很多人都会蹦出“外部排序”，但是却恰有“位图数据结构法”如此巧妙令人拍案叫绝的,这得益于问题的分析到位，数据结构选择得当，...

 

一个新的小问题 

给出一篇文章，统计每个字符出现的次数！！问题不难，但是该怎么解决？

 

• 分析：仔细看，字符无非是ascii表中的可打印的字符，数据结构选择应该是一个struct，里面包含每个字符c和字符出现次数cnt。这个想法很中规中矩。
• 仔细分析：字符的ascii值是固定而且是连续的，是不是可以仿照“位图数据结构法”的方法？上面的“位图数据结构法”用到了bool数组，但是只能记录数据是否出现，也就是说对多次出现的数据无法判断，所以把bool变为int就ok了，数组的下标就是每个ascii字符的值！

 

总结

有个坏习惯，一道题（可以是一道算法题或者具体的软件），只要有思路，手就有瘾似的放到键盘上，坏毛病，后来才发现。一个软件的开发过程，代码是时间只占了30%左右的时间，前面的架构才是重头戏！所以编程始终是后话。试着在做题之前，在纸上分析问题，写出伪代码，然后才敲键盘，你会发现可以大大减少在电脑面前为某个编程细节而苦恼的时间。当然，你可以完全从“纸和笔”中完全解脱出来，代之以mspaint！

 

本文完 Thursday, March 29, 2012 

捣乱小子 http://daoluanxiaozi.cnblogs.com/