希尔排序(一种分组插入排序)
目录:
为什么要用?
希尔排序是直接插入排序的一种更高效的改进版本,是一种分组插入排序,而效率的优劣跟它所使用的步长序列有直接关系。
1、时间复杂度: 平均情况:O(nlog2n) 根据步长序列的不同而不同、最坏情况O(nlog2n) 根据步长序列的不同而不同 ,最好情况O(n)
2、空间复杂度: O(1)
3、稳定性: 不稳定
4、复杂度:较直接插入排序复杂
适用场景: 有研究表明“比较在希尔排序中是最主要的操作,而不是交换。”用已知最好的(塞奇威克(Sedgewick)提出的)步长序列的希尔排序比直接插入排序要快,甚至在小数组中比快速排序和堆排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
原理是什么?
原理描述:
插入排序由来已久了,相信看过 直接插入排序 的同学已经对插入排序有了一定的了解,聪明的同学肯定发现了它的两个规律:
1、 对几乎已经排好序的数据操作效率特别高,甚至可以达到线性O(n)
2、 对于一般的无序数据效率低,特别是逆序数据。
那么是不是有什么方法可以提高它的效率呢? 答案是肯定的。整个直接插入排序的过程可以理解为,每找到一个小数就把它插入到前面来,而大数就相应的向后挤的过程,而大数自己是不会往后走的,也就是说每个小数在向前移动的过程中都要与前面的大数进行比较和交换操作,
就好像每个小个子要想去往正确的位置都需先越过前面的大个子,多么苦逼的一件事。。。
人们肯定会想如果大的数一开始就在后面那就好了,有句话叫“没有条件,创造条件也要上”,那就先上数组变的相对有序,在用直接插入排序就好啦! 具体办法就是把数据分组,组内排序,然后再次 数据分组+组内排序,且分组数量递减,直到分组数为1,也就是直接插入排序啦! 这就是 希尔排序,也称递减增量排序算法的思想啦!
希尔排序的排序效率和选择步长序列有直接关系,相关步长序列如下,目前最好的序列是 4、塞奇威克(Sedgewick) 的步长序列(摘自维基百科)
1、希尔(Shell)原始步长序列:N / 2,N / 4,...,1(重复除以2);
2、希伯德(Hibbard)的步长序列:1,3,7,...,2 k - 1;
3、克努特(Knuth)的步长序列:1,4,13,...,(3 k - 1)/ 2;
4、塞奇威克(Sedgewick) 的步长序列:1,5,19,41,109,....
它是通过交织两个序列的元素获得的: 步长序列数组下标 n 从0开始
n偶数用 :1,19,109,505,2161,...,9(4 k - 2 k)+ 1,k = 0,1,2,3,...
n奇数用 :5,41,209,929,3905,...。k + 2(2 k + 2 - 3)+ 1,k = 0,1,2,3,...
例如 按步长序列 [1,3,5,...] 对数组[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ] 进行希尔排序,首先按步长为5 进行分组,每行为一个分组得到:
13 25 45 10 14 59 27 94 94 73 33 65 25
82 23 39
然后对每行分组进行排序得到:
10 13 25 45 14 27 59 73 94 94 25 33 65
23 39 82
然后再按步长为3进行分组,每行为一个分组得到:
10 25 27 39 94 45 14 23 94 25 65 73 13 33 59 82
对每行分组进行排序得到:
10 25 27 39 45 94 14 23 25 65 94 13 33 59 73 82
至此初始数组:
[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]
而现在的数组:
[ 10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94 ]
在来一次直接插入排序或说事步长为1的分组并排序就得到最终结果了
10 13 14 23 25 25 27 33 39 45 59 65 73 82 94 94
看起来 比直接分组排序 多了些步骤,而实际上 是让一些小数跳过了一些比较和交换操作,直接从后面跳到了前面,从而提高了效率
在分组中的排序步骤同 直接分组排序如下:
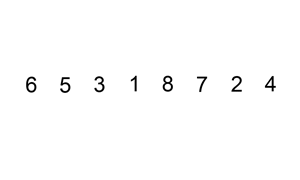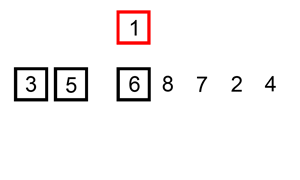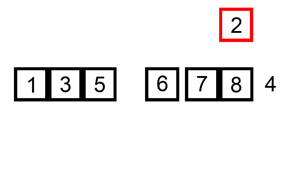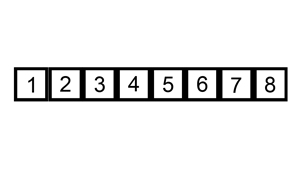
宏观效果:

怎样去实现?
使用已知的最好的由 塞奇威克(Sedgewick) 提出的步长序列:1,5,19,41,109,....
它是通过交织两个序列的元素获得的: 步长序列数组下标 n 从0开始
n偶数用 :1,19,109,505,2161,...,9(4 k - 2 k)+ 1,k = 0,1,2,3,...
n奇数用 :5,41,209,929,3905,...。k + 2(2 k + 2 - 3)+ 1,k = 0,1,2,3,...
java 实现代码:
import java.lang.Math; class shell_sort { // 塞奇威克(Sedgewick) 步长序列函数, 传入数组长度(最大分组个数不可超过数组长度) public static int[] Sedgewick(int length) { int[] arr = new int[length]; int n,i = 0,j = 0; for(n = 0; n < length; n++) { if(n % 2 == 0) { arr[n] = (int) (9 * ( Math.pow(4, i) - Math.pow(2, i) ) + 1); i++; } else { arr[n] = (int) (Math.pow(2, j+2) * ( Math.pow(2, j+2) - 3 ) + 1); j++; } if(arr[n] >= length) { break; } } int[] a = new int[n]; for(int k = 0; k < a.length; k++){ a[k] = arr[k]; } System.out.println("步长序列:"); printArray(a,0,1); return a; } public static void shell(int[] arr){ int[] sedgewick = Sedgewick(arr.length);// 得到塞奇威克(Sedgewick) 步长序列数组 int s,k,i,j,t; // 循环出所有步长 for(s = sedgewick.length -1 ; s >= 0 ; s--){ // 步长为sedgewick[s] 即分为 sedgewick[s] 个组 System.out.println("分"+ sedgewick[s] +"组"); for(k = 0; k < sedgewick[s]; k++){ System.out.println("第"+ (k+1) +"组排序:"); // 对每组数据进行排序 printArray(arr,k,sedgewick[s]); for(i = k + sedgewick[s]; i < arr.length; i += sedgewick[s]){ // 分组中,按插入排序排序数据,交换数据按步长 sedgewick[s] t = arr[i]; j = i - sedgewick[s]; while(j >= 0 && arr[j] > t){ arr[j + sedgewick[s]] = arr[j]; j-=sedgewick[s]; } arr[j+sedgewick[s]] = t; printArray(arr,k,sedgewick[s]); } System.out.println(); } } } public static void main (String[] args) throws java.lang.Exception { int[] arr = { 13,14,94,33,82,25,59,94,65,23,45,27,73,25,39,10}; System.out.println("原数据:"); printArray(arr,0,1); shell(arr); } public static void printArray(int[] arr,int i, int j){ for(int n = i ; n < arr.length; n+= j){ System.out.print(arr[n]+" "); } System.out.println(); } }
输出结果 :
原数据:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
步长序列:
1 5
分5组
第1组排序:
13 25 45 10
13 25 45 10
13 25 45 10
10 13 25 45
第2组排序:
14 59 27
14 59 27
14 27 59
第3组排序:
94 94 73
94 94 73
73 94 94
第4组排序:
33 65 25
33 65 25
25 33 65
第5组排序:
82 23 39
23 82 39
23 39 82
分1组
第1组排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
10 14 25 73 23 13 27 94 33 39 25 59 94 65 82 45
10 14 23 25 73 13 27 94 33 39 25 59 94 65 82 45
10 13 14 23 25 73 27 94 33 39 25 59 94 65 82 45
10 13 14 23 25 27 73 94 33 39 25 59 94 65 82 45
10 13 14 23 25 27 73 94 33 39 25 59 94 65 82 45
10 13 14 23 25 27 33 73 94 39 25 59 94 65 82 45
10 13 14 23 25 27 33 39 73 94 25 59 94 65 82 45
10 13 14 23 25 25 27 33 39 73 94 59 94 65 82 45
10 13 14 23 25 25 27 33 39 59 73 94 94 65 82 45
10 13 14 23 25 25 27 33 39 59 73 94 94 65 82 45
10 13 14 23 25 25 27 33 39 59 65 73 94 94 82 45
10 13 14 23 25 25 27 33 39 59 65 73 82 94 94 45
10 13 14 23 25 25 27 33 39 45 59 65 73 82 94 94
在线测试地址 :https://www.shucunwang.com/RunCode/java/#id/b8f9435e80e07068633bc3adf17c9cc7
开源代码地址 :https://git.oschina.net/ITxiaoyan/SortAlgorithm
更多排序算法请查看:排序算法笔记 http://www.cnblogs.com/daohuoren/p/6605077.html
2017-03-25



