文本分类学习 (四) 特征选择之卡方检验
前言:
上一篇提到了特征提取,或者叫做降维。在文本分类中,特征提取算法的优劣对于文本分类的结果具有非常大的影响。 所以选择效果好的特征提取算法是文本分类前中很重要的步骤。于是这篇就对卡方检验做一个介绍。这是一个效果很好的特征提取方法。
之前对卡方检验做过介绍:卡方检验是通过对特征进行打分然后排序,选择排名靠前的特征来表示文本。
目录:
- 文本分类学习(一)开篇
- 文本分类学习(二)文本表示
- 文本分类学习(三)特征权重(TF/IDF)和特征提取
- 文本分类学习 (四) 特征选择之卡方检验
一:卡方检验的介绍
1.接下来简单介绍一下卡方检验:
(官方定义)
卡方检验是以χ2分布为基础的一种常用假设检验方法,它的无效假设H0是:观察频数与期望频数没有差别。该检验的基本思想是:首先假设H0成立,基于此前提计算出χ2值,它表示观察值与理论值之间的偏离程度。根据χ2分布及自由度可以确定在H0假设成立的情况下获得当前统计量及更极端情况的概率P。如果当前统计量大于P值,说明观察值与理论值偏离程度太大,应当拒绝无效假设,表示比较资料之间有显著差异;否则就不能拒绝无效假设,尚不能认为样本所代表的实际情况和理论假设有差别。(摘自智库百科)
(通俗的来讲)
卡方检验的思想是通过观察值和理论值之间的偏差来判断理论值的正确率是多少。如果正确率很大我们就认为理论值是正确的。所以我们一开始要设定一个理论值,这个理论值是我们根据自己的假设计算而来。
2.卡方检验的基本公式:
卡方检验的基本公式,也就是χ2的计算公式,也就是观察值和理论值之间的偏差

先介绍下这个公式是如何得来的吧
其中A代表观察频数(就是观察值),E代表期望频数(就是理论值,我们一开始做的那个假设得到的值)
- 那么第一步,观察值和理论值之间的偏差,就是二者的差。将多个观察值和理论值的偏差求和
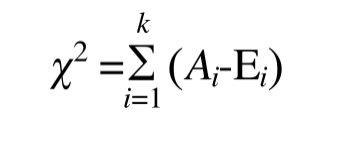
- 这样确实可以表示偏差,但是多个观察值和理论值,且差值有正有负,那么就会相互抵消,如果抵消为0,本来有偏差的,现在变成没有偏差 了。所以第二步,加上平方之后再求和
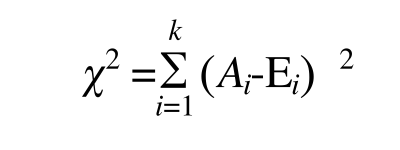
- 这样确实可以表示偏差,但是多个观察值和理论值,且差值有正有负,那么就会相互抵消,如果抵消为0,本来有偏差的,现在变成没有偏差 了。于是第三步,在平之后再除以理论值之后再求和,这样不会因为理论值的大小而影响偏差的计算了
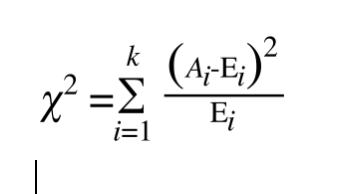
越是得到了最终χ2的计算公式。再回到这个式子:
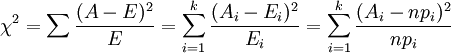
A 为观察值,E为理论值,k为观察值的个数,最后一个式子实际上就是具体计算的方法了 n 为总的频数,p为理论频率,那么n*p自然就是理论频数(理论值)
3.卡方分布:
可以看出当观察值和理论值十分接近的时候,也就是我们做的假设是正确的时候,χ2的值就越趋近于0,也就是说我们计算的偏差越小,那么假设值就越可能是对的,那么偏差值越大,假设值就越不准确。那么到底多大才算不准确,有没有个衡量的数值标准呢?答案是有:卡方分布。
于是我们再看到官方说的第一句话:卡方检验是以χ2分布为基础的一种常用假设检验方法
χ2分布,就叫做卡方分布。那么卡方分布是个什么东西呢?官方定义:
若k 个随机变量Z1、……、Zk 相互独立,且数学期望为0、方差为 1(即服从标准正态分布),则随机变量X
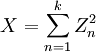
被称为服从自由度为 k 的卡方分布,记作
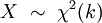
官方的定义我们也不管了,公式也不管了。直接用Matlab 画出卡方分布的图来,我们通过直观图,来看懂卡方分布:
我写的Matlab的卡方分布图的代码:
x=0:0.01:50; y=chi2pdf(x,1); y1=chi2pdf(x,4); y2=chi2pdf(x,10); y3=chi2pdf(x,20); y4=chi2pdf(x,50); plot(x,y,'-r',x,y1,'-.b',x,y2,':k',x,y3,'--g',x,y4,'-m'); legend('Freedom 1','Freedom 4','Freedom 10','Freedom 20','Freedom 100'); axis([0,50,0,0.2]);
于是得到这样的图:

先看上图中的Freedom 这里有5条线,分别对应Freedom=1, 4, 10, 20 , 100 。这个Freedom 就是自由度(我英语不好),俗称:个式子中独立变量的个数。(具体的后面再说到)。 就是卡方分布官方定义中的k,k个符合标准正太分布的随机变量。先不管这个自由度是干嘛,也不管在实际应用中是怎么计算出来的。我们挑一条曲线Freedom = 1 来看:
x 横坐标 其实就是我们前面利用卡方检验公式计算出来的偏差χ2 而y 纵坐标表示假设的正确的概率。可以看到当χ2 的值越小,假设正确的可能性无限大,值越大假设正确的可能性无限小,正好验证了卡方检验的公式。(文章的最后会放上一个卡方分布的表格)。
现在我们回过头看自由度,通过观察图可以发现,不同自由度的卡方分布可以说差别很多。当自由度为1时,卡方分布式一个倾斜的曲线,当自由度逐渐增大是,卡方分布逐步变的平缓,两头矮,中间高。对没错,随着自由度越来越大,卡方分布会越来越接近正态分布(因为我们看到卡方分布的定义,卡方分布本来就是由k个标准正太分布的方差形成的分布)。这个时候疑问就来了,当自由度为1的时候,很好理解χ2 越小,概率越大,χ2 越大概率越小,这个好理解通过卡方检验的公式可以看出。当自由度越大的时候,怎么χ2 越大,对应的概率先是变大,然后再是变小呢?还有另一个问题,卡方检验的自由度又是怎么算的呢?前面说过,自由度其实就公式中独立变量的个数,它可以表示变量的变化范围。这里实在不想通过公式推导,卡方分布自由度是怎么得出,并且表示的是什么,太繁琐,不易理解,更重要的是我根本不会。
二:实例,通过卡方检验进行特征选择
1.四表格
带着这两个问题,我们到实际的例子中去查看。
突然想起来,这篇文章是在说卡方检验在文本分类的特征提取中的应用。所以例子不能跑题,我们看下面的四格图表(百度四格图表+卡方检验 你会发现有很多例子。如果把四格换成八格,就很少了。事实上特征提取我们用四格图表就够了。)
我这个例子和网上的都大同小异,也不能照搬别人,就自己造一点数据。
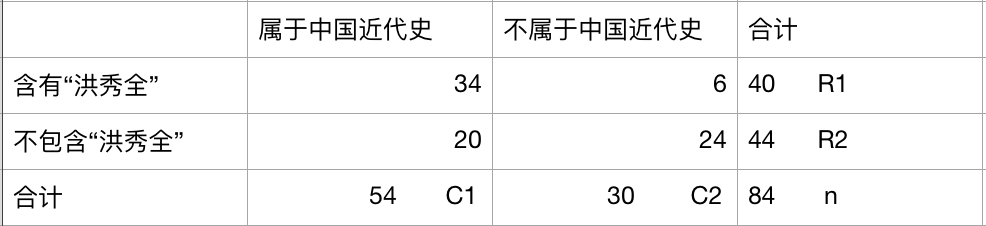
这是一个四格表,表示我在把文本一通分析之后发现 包含"洪秀全"这个词且属于中国近代史的有34个文本,而包含这个词不属于中国近代史的有6文本.........
通过这个四格表的提供信息,我们来检验词"洪秀全"和中国近代史类的文本的关系。
我加入C1 C2 R1 R2 分别表示第1列的合计,第2列的合计,第1行的合计,第2行的合计。n表示总数。
第一步我们应该做啥?肯定是先做一个假设啊,我们假设"洪秀全"和中国近代史类的文本没有任何关系(为什么不假设有关系呢?)
然后我们去确认观察值,和理论值,确定好了之后不就可以算偏差了嘛!
那么观察值是什么?很显然,观察值就是表格中的数字,表示实际我们观察到的值。观察值有几个呢?很显然是4个,因为是4格表啊。分别是:
34 (含有"洪秀全"属于中国近代史); 6 (含有"洪秀全"不属于中国近代史); 20 (不含有"洪秀全"属于中国近代史);24(不含有"洪秀全"不属于中国近代史)
那么理论值是什么呢?理论值也是4个,和观察值一一对应。理论值怎么计算呢?当然是通过假设来计算。
我们假设"洪秀全"这个词和中国近代史类的文本没有任何关系,那么就表示有无"洪秀全"对它是不是中国近代史类的文本没有影响。根据这个假设,我们来算第一个观察值(含有"洪秀全"属于中国近代史)对于的理论值。我们设为 E11,表示第一行第一列的理论值。
根据假设,我们可以先算出一个文本出现"洪秀全"的概率,然后用中国近代史的文本个数乘以这个概率就得到了理论值,很好理解的普通概率问题。(想一想,这一起是不是建立在我们的假设的基础上。如果假设是二者不相关,那么理论值应该怎么算?你会发现根本不知道怎么算)
出现"洪秀全"的概率 = 包含"洪秀全"的文本 / 总文本 这很好理解。
于是我们可以得出第一个理论值E1 = E11 (第一个1表示第一个理论值,后来两个1表示四格表中第1行第1列,显然二者是等价的)
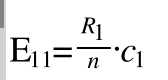
由次可以类推Epq 表示p行q列的理论值
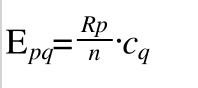
这个时候我们就可以算出四格表中的理论值了,我们可以先把四个理论值算出来,然后带入卡方检验的公式中去求偏差。当然也可以把Epq 带入卡方检验的公式中然后直接根据公式来算

其实没什么复杂的 ,会基础的概率知识就一下能看明白了。于是我们就可以算出偏差了。
通过公式可以算出:
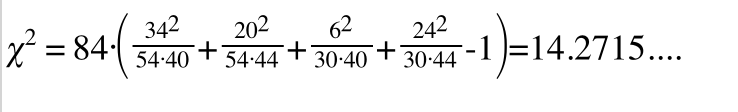
偏差值是14.2715,下一步呢?当然是去查卡方分布表。在查看卡方分布表的时候,我们发现还有个自由度的问题,那么问题来了,我们上面的四格表中自由度是多少呢?答案是(p-1)*(q-1)也就是(行数-1)*(列数-1) 。为什么是这么算的呢?这个暂时先不管了,根据查表我们得知自由度设为df,df为1的卡方分布如下:

可以看到v=1 ,χ2 = 3.84 是对应的P是0.05 ,再看看上面的函数图,的确如此。为什么0.05要涂颜色呢?这是因为在卡方分布中概率小于0.05的叫做一个拒绝域,也就是说如果你算出来的P小于0.05,那么原假设就不成立。在卡方分布函数图中表示就是一个小尾巴:

前面我们算出来的值是14.2715 很明显已经大约3.84 也就是P < 0.05 也就是说原假设成立的概率小于5% 那么就意味着假设不成立,于是我们可以得出结论"洪秀全"和中国近代史是有关系的。
2.自由度的问题
这个四格表的案例就是通过卡方检验在文本分析中的应用。
再回到前面的两个问题:
- 为什么自由度不一样,卡方分布的区别就很大,自由度越大卡方分布越接近正太分布
- 自由度是怎么算的。
先回答第二个问题,上面说到过自由度=(行数-1)*(列数-1) 。自由度指的是计算某一统计量时,取值不受限制的变量个数。通常df=n-k。其中n为样本数量,k为被限制的条件数或变量个数。
在这里行数是两个变量,n=2 ,四格表中的限制条件数k=1,因为四个表中有一个限制条件:总数一定。所以自由度为2-1=1,
列数也同理。所以自由度df = (行数-1)*(列数-1)
3.八格表
再看第一个问题:看一个八格表:
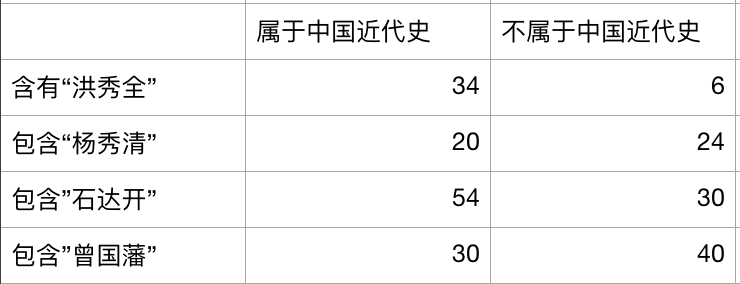
我们假设"洪秀全","杨秀清","石达开","曾国藩"对于文本是否为中国近代史的影响程度是不一样的。
自由度df = 3
这样就可以理解为什么df越大就越符合正太分布。因为"洪秀全","杨秀清","石达开","曾国藩"这四个词对文本是否为中国近代史影响都非常小,查看前面的公式就是(A-E)的偏差都很小,得出的χ2 越小,这个时候意味着这四个词的影响程度是一样的,也即通过卡方分布计算的假设成立概率是很小的,在上面的卡方分布函数图中就可以看出属于卡方分布左边的小尾巴。同理当这个四个词的影响都很大的时候,假设成立的概率也是很小,所以属于卡方分布的右边小尾巴。
这样通过例子就好理解一点了。
三,利用卡方检验用来特征选择
说到这里,我们再回头看下卡方检验在特征选择中的应用。通篇大部分在说卡方检验,而实际应用到特征选择中的时候,我们不需要知道自由度,不要知道卡方分布,我们只需要根据算出来的χ2 进行排序就好了,越大我们就越喜欢!挑选最大的一堆,于是就完成了利用卡方检验来进行特征提取。
一般在四格表中如果第一行,第一列的值表示为A,第二行第二列的值表示为B,第三行第三列的值表示为C,第四行第四列的值表示为D
在四格表中的卡方检验公式可以变换为:

上面也说了,对于文本分类我们只关心排序,不要求算出具体的值,对于每个词,n是不变的,(A+C)也就是属于中国近代史的文本,是不变的,(B+D)也是不变的。所以可以化简:
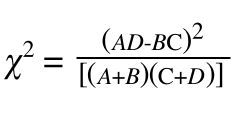
然而我们发现在四格表中,我们只关心了出现"洪秀全"的文本,而没有提及"洪秀全"出现了几次,也就是忽略了词频。这是卡方检验的低词频性的缺点,所以实际应用的时候还需要结合词频的因素,考虑进去。
四,结语
本来博客的题目叫做“特征选择之卡方检验”,我现在想改名字叫做“卡方检验之特征选择”。
下一篇就要开始实战了,利用JIEba分词,对训练集进行分析再特征选择,最后构造出一个非常合适的词向量。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)