联合权值

问题 B: 联合权值

时间限制: 1 Sec  内存限制: 128 MB
提交: 138  解决: 21
[提交] [状态] [讨论版] [命题人:admin]

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。
请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

 

输入

第一行包含1 个整数n 。
接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。
最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

 

输出

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值
和所有联合权值之和。由于所有联合权值之和可能很大，[b]输出它时要对10007 取余。

 

样例输入

复制样例数据

5
1 2
2 3
3 4
4 5
1 5 2 3 10

样例输出

20 74

 

提示

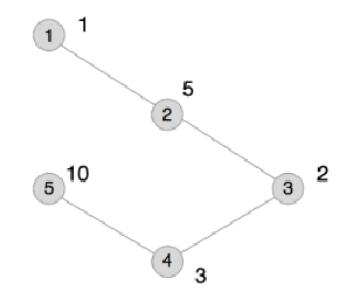
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

 

 

对于 30%的数据，1 < n ≤ 100；

对于 60%的数据，1 < n ≤ 2000；

对于 100%的数据，1 < n ≤ 200,000，0 < Wi ≤ 10,000。 

思路：先枚举以每个点为中轴点，找出与其直接相连的点，记录总值和最大值，判断一下是否有多个最大值，然后枚举每个点所对应的另一边的点，注意体会这两次枚举的点的差别。

#include<bits/stdc++.h>
#define REP(i, a, b) for(int i = (a); i <= (b); ++ i)
#define REP(j, a, b) for(int j = (a); j <= (b); ++ j)
#define PER(i, a, b) for(int i = (a); i >= (b); -- i)
using namespace std;
const int maxn=2e6+666;
template <class T>
inline void rd(T &ret){
    char c;
    ret = 0;
    while ((c = getchar()) < '0' || c > '9');
    while (c >= '0' && c <= '9'){
        ret = ret * 10 + (c - '0'), c = getchar();
    }
}
long long w[maxn],r,s,t,dis[maxn],tot[maxn],mx[maxn],pos[maxn],cover[maxn],ans,mans;
int head[maxn],l;
struct node{
      int v,nx;
}p[maxn];
long long n,m;
void addedge(int x,int y){
     p[++l].v=x,p[l].nx=head[y],head[y]=l;
     p[++l].v=y,p[l].nx=head[x],head[x]=l;
}

int main(){
    rd(n);
    REP(i,1,n-1){
       int a,b;
       rd(a),rd(b);
       addedge(a,b);
    }
    REP(i,1,n)rd(w[i]);
    REP(i,1,n){
        for(int j=head[i];j;j=p[j].nx){
            tot[i]+=w[p[j].v];
            if(mx[i]<w[p[j].v])mx[i]=w[p[j].v],pos[i]=p[j].v,cover[i]=0;
            else if(mx[i]==w[p[j].v])cover[i]=1;
        }
    }
    REP(i,1,n){
         for(int j=head[i];j;j=p[j].nx){
            ans=(ans+w[i]*(tot[p[j].v]-w[i]))%10007;
            if(cover[p[j].v]||pos[p[j].v]!=i)mans=max(mans,w[i]*mx[p[j].v]);
         }
    }
    cout<<mans<<' '<<ans<<endl;
    return 0;
}

 

点，统计答案就好了。