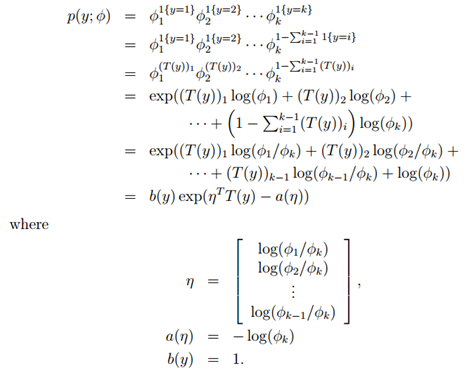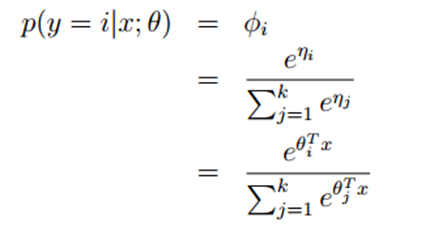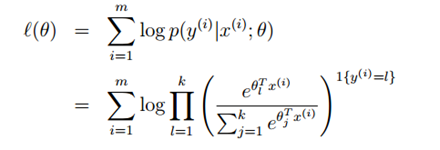广义线性模型(Generalized Linear Models)
在线性回归问题中,我们假设![]() ,而在分类问题中,我们假设
,而在分类问题中,我们假设![]() ,它们都是广义线性模型的例子,而广义线性模型就是把自变量的线性预测函数当作因变量的估计值。很多模型都是基于广义线性模型的,例如,传统的线性回归模型,最大熵模型,Logistic回归,softmax回归。
,它们都是广义线性模型的例子,而广义线性模型就是把自变量的线性预测函数当作因变量的估计值。很多模型都是基于广义线性模型的,例如,传统的线性回归模型,最大熵模型,Logistic回归,softmax回归。
指数分布族
在了解广义线性模型之前,先了解一下指数分布族(the exponential family)
指数分布族原型如下
如果一个分布可以用上面形式在表示,那么这个分布就属于指数分布族,首先来定义一下上面形式的符号:
η:分布的自然参数(natural parameter)或者称为标准参数(canonical parameter)
T (y):充分统计量,通常用T(y) = y
a(η):对数分割函数(log partition function)
:本质上是一个归一化常数,确保
概率和为1。
当给定T时,a、b就定义了一个以η为参数的一个指数分布。我们变化η就得到指数分布族的不同分布。
论证伯努利分布和高斯分布为指数分布族
![]() ,伯努利分布均值φ,记为Bernoulli(φ),y ∈ {0, 1},所以p(y = 1; φ) = φ; p(y = 0; φ) = 1 − φ
,伯努利分布均值φ,记为Bernoulli(φ),y ∈ {0, 1},所以p(y = 1; φ) = φ; p(y = 0; φ) = 1 − φ
对比指数分布族的表达式可以得到:
η = log(φ/(1-φ)) 我们将φ用η表示,则:φ=1/(1+e-η),是不是发现和sigmoid函数一样了。
这就表明,当我们给定T,a,b,伯努利分布可以写成指数分布族的形式,也即伯努利分布式指数分布族。
对比指数分布族,我们得到:
因为高斯分布的方差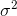 与假设函数无关,因而为了计算简便,我们设方差
与假设函数无关,因而为了计算简便,我们设方差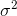 =1,这样就得到:
=1,这样就得到:
所以这也表明,高斯分布也是指数分布族的一种。
构造广义线性模型(Constructing GLMs)
怎么通过指数分布族来构造广义线性模型呢?要构建广义线性模型,我们要基于以下三个假设:
- 给定特征属性
和参数
后,
的条件概率
服从指数分布族,即
。
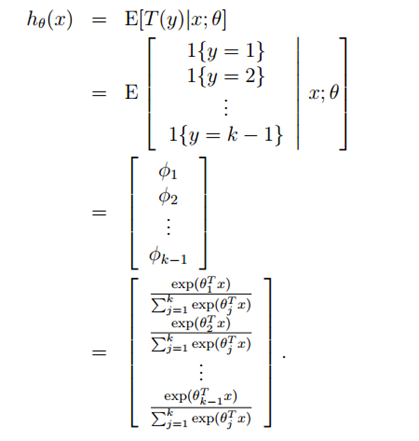
- 预测
的期望,即计算
。 #h(x) = E[y|x]
与
之间是线性的,即
。
构建最小二乘模型
回顾一下,在线性回归中,代价函数y是通过最小二乘法得到的。下面通过广义线性模型来构造最小二乘模型。
线性回归中,假设y|x;θ服从高斯分布N(μ,σ2)N(μ,σ2),根据我们前面的推导,我们知道µ = η,所以根据三个假设有
说明:
第二个等号根据高斯分布的期望为μ得到
第三个等号根据我们前面推到可得,也即假设1
第四个等号根据假设3得到。
至此,最小二乘模型构建完成,也即为线性回归中使用的线性模型的来源。接下来的工作就是利用梯度下降,牛顿方法求解Θ
构建逻辑回归
逻辑回归可以用来解决二分类问题,二分类问题的目标函数是离散值,通过统计学知识我们知道可以选择伯努利分布来构建逻辑回归的模型
在前面的论证中我们得到η = log(φ/(1-φ)) 我们将φ用η表示,则:φ=1/(1+e-η)。根据三个假设,我们有
构建完成,这就是逻辑回归中使用的模型。
构建Softmax Regression
现在我们考虑一个多分类问题,也即响应变量y有k个值,即y ∈{1 2, . . . , k},首先我们来证明多项分布也同样属于指数分布族。
多分类模型的输出结果为该样本属于k个类别的概率,我们可以用φ1, . . . , φk来表示这k个样本输出的概率。φ1, . . . , φk满足![]() ,但是这样参数就显得有些冗余了,所以我们用φ1, . . . , φk−1来表示,则
,但是这样参数就显得有些冗余了,所以我们用φ1, . . . , φk−1来表示,则![]()
定义T(y)∈Rk-1如下:
注意:
在这里T(y)就不等于y了,在这里它是一个k-1维的向量,而不是一个实数。规定(T (y))i表示向量T(y)中第i个元素
另外,引入一个新的符号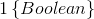 ,如果大括号内为true,则该式等于1,反之为0,例如1{2 = 3} = 0,1{3 =5 − 2} = 1,
,如果大括号内为true,则该式等于1,反之为0,例如1{2 = 3} = 0,1{3 =5 − 2} = 1,
所以有:
所以这样,多项式分布我们也可以写成指数分布族的样式,也即,多项分布也是指数分布族。所以我们可以用广义线性模型来拟合了
通过η的表达式可以得到:ηi=log(φi/φk) 这是ηi关于φi的表达式,将它转化为φi关于ηi,为了方便,我们令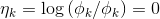 ,所以有
,所以有
所以可以求得![]() ,代入上图红色方框的等式中,求得
,代入上图红色方框的等式中,求得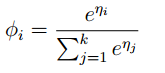 ,这个
,这个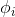 关于
关于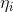 的的函数称为Softmax函数(Softmax Function)
的的函数称为Softmax函数(Softmax Function)
下面我们使用广义线性构造模型
根据假设3,有ηi = θiT x (for i = 1, . . . , k − 1), where θ1, . . . , θk-1 ∈ Rn+1 同样在这里我们定义θk = 0 所以可以得到:ηk = θkT x = 0
所以模型在给定x的条件下y的分布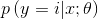 为:
为:
应用在多分类模型上的这个模型称之为softmax regression,它是逻辑回归的一般化。
对于假设函数,我们有假设2可以得到
所以现在求解目标函数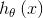 的最后一步就是参数的拟合问题。最大似然估计得到
的最后一步就是参数的拟合问题。最大似然估计得到
最大似然函数来求解最优的参数θ,跟前面介绍的一样,可以使用梯度上升或者牛顿方法。



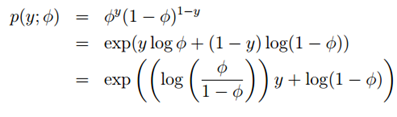

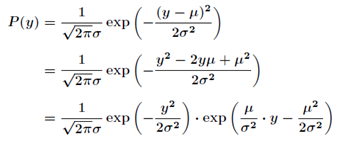
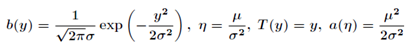
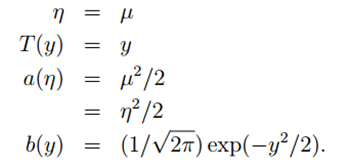
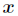 和参数
和参数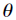 后,
后, 的条件概率
的条件概率 服从指数分布族,即
服从指数分布族,即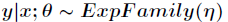 。
。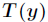 的期望,即计算
的期望,即计算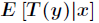 。 #h(x) = E[y|x]
。 #h(x) = E[y|x] 与
与 之间是线性的,即
之间是线性的,即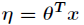 。
。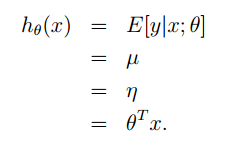
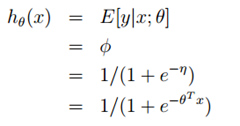
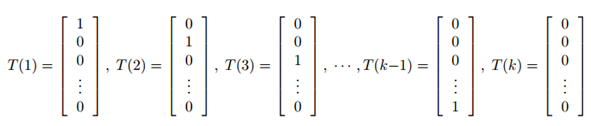
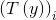 与
与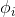 关系可以表示为:
关系可以表示为: