【2016蓝桥杯省赛】试题C++ B组试题
一、 煤球数目
作答：171700
#include <iostream> using namespace std; int main() { int sum=0,x=0; for(int i=1;i<=100;i++){ x+=i; sum += x; } cout<<sum; }
二、 生日蜡烛
作答：26
#include <iostream> using namespace std; int main() { for(int i=0;i<236;i++){ int sum=0; for(int j=i;sum<236;j++){ sum+=j; } if(sum==236){ cout<<i; break; } } }
三、 凑算式
纯暴力+剪枝，剪成这样大概30s就跑出来了，觉得剪得差不多了，跑起来试试，反正跑的时候又不耽误继续写。
作答：29
#include <iostream> #include <math.h> using namespace std; int gcd(int x, int y) { if (y == 0)return x; return gcd(y, x%y); } int lcm(int x, int y) { return x * y / gcd(x, y); } void simp(int &x, int &y) { int t = gcd(x, y); x /= t; y /= t; } void add(int &x1, int &y1, int x2, int y2) { int t = lcm(y1, y2); x1 = x1 * t / y1 + x2 * t / y2; y1 = t; simp(x1, y1); } int repeat(int A, int B, int C, int DEF, int GHI) { int a[10] = { 0 }; a[A]++; a[B]++; a[C]++; while (DEF > 0) { a[DEF % 10]++; a[GHI % 10]++; GHI /= 10; DEF /= 10; } if (a[0] > 0)return 1; for (int i = 0; i < 10; i++) { if (a[i] > 1)return 1; } return 0; } int main() { int count = 0; for (int A = 1; A <= 9; A++) { for (int B = 1; B <= 9; B++) { if (A == B)continue; for (int C = 1; C <= 9; C++) { if (A == C || B == C || (A + B / (float)C > 10))continue; for (int DEF = 123; DEF <= 987; DEF++) { for (int GHI = 123; GHI <= 987; GHI++) { if (repeat(A, B, C, DEF, GHI)) continue; else { int a = A, b = B, c = C, def = DEF, ghi = GHI; add(b, c, def, ghi); if (c == 1 && b == 10 - a) { cout << A << "+" << B << "/" << C << "+" << DEF << "/" << GHI << "=" << 10 << endl; count++; } } } } } } } cout << count << endl; return 0; }
四、 快速排序
快速排序的partition过程，基本算法是很重要的。
swap(a,p,j);
五、 抽签
看到题目，第一反应，这肯定是个递归，蒙蒙看，看终止条件K==N，输出条件m==0，
第一次试，f(a,k+1,m-1,b); 不对。
第二次试，f(a,k+1,m-j,b); 半分钟解决。。。。
其实仔细看下，也很简单，k表示第几个国家，m表示当前还剩多少空位。当然实际循环里，添加进去b数组的不止5个，多出来的，b[M] = 0; 都给砍掉了。
f(a,k+1,m-j,b);
六、方格填数
1580
#include <iostream> #include <stdio.h> #include <algorithm> using namespace std; int f1(int a[][6], int x, int y) { for (int i = x - 1; i <= x + 1; i++) for (int j = y - 1; j <= y + 1; j++) { if (i == x && y == j)continue; if (a[x][y] + 1 == a[i][j] || a[x][y] - 1 == a[i][j])return 1; } return 0; } int f2(int x, int y) { if (x == y + 1 || x == y - 1 || x == y)return 1; return 0; } int main() { int a[5][6] = { -2 }; int count = 0; for (int a0 = 0; a0 <= 9; a0++) { for (int a1 = 0; a1 <= 9; a1++) { if (f2(a0, a1))continue; for (int a2 = 0; a2 <= 9; a2++) { if (a2 == a0 || f2(a2, a1))continue; for (int a3 = 0; a3 <= 9; a3++) { if (a3 == a2 || a3 == a1 || f2(a3, a0))continue; for (int a4 = 0; a4 <= 9; a4++) { if (f2(a4, a3) || a4 == a2 || f2(a4, a1) || f2(a4, a0))continue; for (int a5 = 0; a5 <= 9; a5++) { if (f2(a5, a4) || a5 == a3 || f2(a5, a2) || f2(a5, a1) || f2(a5, a0))continue; for (int a6 = 0; a6 <= 9; a6++) { if (f2(a6, a5) || a6 == a4 || a6 == a3 || f2(a6, a2) || f2(a6, a1) || a6 == a0)continue; for (int a7 = 0; a7 <= 9; a7++) { if (a7 == a6 || a7 == a5 || f2(a7, a4) || f2(a7, a3) || a7 == a2 || a7 == a1 || a7 == a0)continue; for (int a8 = 0; a8 <= 9; a8++) { if (f2(a8, a7) || a8 == a6 || f2(a8, a5) || f2(a8, a4) || f2(a8, a3) || a8 == a2 || a8 == a1 || a8 == a0)continue; for (int a9 = 0; a9 <= 9; a9++) { if (f2(a9, a8) || a9 == a7 || f2(a9, a6) || f2(a9, a5) || f2(a9, a4) || a9 == a3 || a9 == a2 || a9 == a1 || a9 == a0)continue; count++; } } } } } } } } } } cout << count << endl; }
七、剪邮票
如
, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
比如，
，
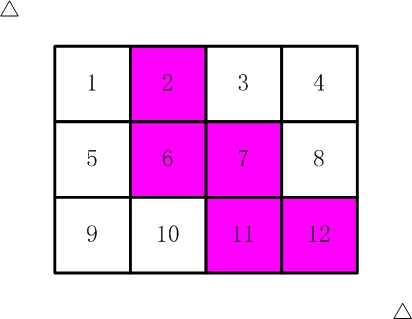中，粉红色所示部分就是合格的剪取。
请你计算，一共有多少种不同的剪取方法。
这5个点一定是个连通图，BFS更好写。
核心思想：1. BFS判定给定的5个位置是否符合。
2. 每层循环取不同值，避免重复
#include <iostream> #include <queue> using namespace std; bool BFS(int a, int b, int c, int d, int e) { bool m[13] = {0}; queue<int>q; m[b] = 1; m[c] = 1; m[d] = 1; m[e] = 1; q.push(a); while (!q.empty()) { int i = q.front(); q.pop(); //向上走 if ((i - 4) > 0 && m[i - 4] == 1) { m[i - 4] = 0; q.push(i - 4); } //向下走 if ((i + 4) < 13 && m[i + 4] == 1) { m[i + 4] = 0; q.push(i + 4); } //向右走 if (i != 4 && i != 8 && i + 1 < 13 && m[i + 1] == 1) { m[i + 1] = 0; q.push(i + 1); } //向左走 if (i != 5 && i != 9 && i - 1 > 0 && m[i - 1] == 1) { m[i - 1] = 0; q.push(i - 1); } } for (int i = 1; i < 13; i++) if (m[i])return false; return true; } int main() { int a, b, c, d, e, res = 0; for (a = 1; a <= 8; a++) { for (b = a + 1; b <= 9; b++) { for (c = b + 1; c <= 10; c++) { for (d = c + 1; d <= 11; d++) { for (e = d + 1; e <= 12; e++) { if (BFS(a, b, c, d, e)) { printf("%d %d %d %d %d\n", a, b, c, d, e); res++; } } } } } } cout << res << endl; return 0; }
八、四平方和定理
（1）NC做法，四重循环，死求，能出来，但是时间上，完全不达标。
（2）三重循环：因为第四个数可以由 前三个数和输入的数相剪 得出，省去最后一个循环。效率提升就很显著了。
#include <iostream> #include <math.h> using namespace std; int main() { int x, i, j, k; int sign = 1; cin >> x; double X = sqrt(x); for (i = 0; sign&&i <= X; i++) { for (j = i; sign&&j <= X; j++) { for (k = j; sign&&k <= X; k++) { double L = sqrt(x - i * i - j * j - k * k); if (L == (int)L) { cout << i << " " << j << " " << k << " " << L << endl; sign = 0; } } } } return 0; }
（3）三重循环，将算过的数据存起来 + 剪枝：
#include <iostream> #include <math.h> using namespace std; int main() { int x, i, j, k; int sign = 1; cin >> x; int *arr = new int[x]; memset(arr, 0, x * sizeof(int)); double X = sqrt(x); for (i = 0; sign&&i <= X; i++) { if (!arr[i]) arr[i] = i * i;//i^2没算过，就算好存起来 for (j = i; sign&&j <= X; j++) { if (!arr[j]) arr[j] = j * j;//j^2没算过，就算好存起来 int J = arr[i] + arr[j]; if (J > x) break;//剪枝 for (k = j; sign&&k <= X; k++) { if (!arr[k]) arr[k] = k * k;//k^2没算过，就算好存起来 int K = J + arr[k]; if (K > x) break; double L = sqrt(x - K); if (L == (int)L) { cout << i << " " << j << " " << k << " " << L << endl; sign = 0; } } } } return 0; }
九、交换瓶子
一开始，觉得最快的应该是快速排序的交换过程，后来仔细想下，数据很特殊，最后有序情况下，就是a[i]=i；快速排序还是会进行很多次无用的交换。
就从前面往后直接找，所以下标是1的位置就应该放1号瓶子，以此类推。
正常是一次交换排好一个元素，想要一次排好两个元素，就得数据支持，比如 a [ i ] = j ; a [ j ] = i ；这个交换代码也是可以做到的，所以这就是最少的步数。
#include <iostream> using namespace std; int main() { int n,a[10005]; cin>>n; for(int i = 1; i <= n; i++) cin>>a[i]; int ans = 0; for(int i = 1; i <= n; i++) { while(a[i] != i) //如果数值和下标不相等，直接交换 { swap(a[i],a[a[i]]); ans++; } } cout<<ans<<endl; return 0; }
十、最大比例
首先这个比例一定是 大于 1 ，小于 max/min 的 ，那我们就可以用这个 max/min 不断除以自身的最小素因子，来寻找答案。
思想：
1. 用最大的数 除以 最小的数，得到一个可能的最大比例（A/B）。
2. 从小到大进行遍历。
- 如果第 i 个数乘以A/B小于第 i+1个数，继续乘A/B。
- 如果大于第i+1个数，说明这个比例是不对的（大了），A和B分别除去自己的最小素因子。
3. 遍历一遍之后，会得到一个A/B。但这并不一定是答案，回到第二步，如果整个遍历都没有出现第二部的蓝色字段，出来的就是答案了。
上面的这些过程，时间主要在找素因子上，我们可以分析得到，这个最大的素因子会出现的情况是：X=x^2，X除1以外只有x一个因子，X数值上接近10^12，简单说就是素数表准备到 一百万 就够用了。
#include <iostream> #include <algorithm> #include <set> #include <vector> using namespace std; typedef long long ll; #define N 1000000 int prime[80000]; int M[N+1]; //打素数表 void EulerSieve() { int count = 0; for (int i = 2; i <= N; i++) { if (M[i] == 0) { prime[count++] = i; } for (int j = 0; j < count && prime[j] * i <= N; j++) { M[i*prime[j]] = 1; if (i%prime[j] == 0) break; } } } ll getMinPrimefactor(ll x) { if (x < N&&M[x] == 0)return x; //不知道具体数字，循环终止写大点无所谓，不会做到后面的。 for (int i = 0; i < 80000; i++) { if (prime[i] == 0)return x; if (x%prime[i] == 0)return prime[i]; } } ll gcd(ll a, ll b) { return b ? gcd(b, a%b) : a; } void reduce(ll &x, ll &y) { ll g = gcd(x, y); x /= g; y /= g; } //分数除 void div(ll &x1,ll &y1,ll x2,ll y2) { y1 *= x2; x1 *= y2; reduce(x1, y1); } //分数乘 void mul(ll &x1, ll &y1, ll x2, ll y2) { y1 *= y2; x1 *= x2; reduce(x1, y1); } void check(ll &A,ll &B,set<ll>s,int &flag) { set<ll>::iterator it = s.begin(); while (true) { ll a = *it++, b = 1; if (it == s.end()) return; while (a < *it) { mul(a, b, A, B); } if (a > *it) { B /= getMinPrimefactor(B); A /= getMinPrimefactor(A); flag = true; it--; } //if (a == *it) { // cout << A << "/" << B << endl; //} } } int main() { ll n, t; int flag = true; EulerSieve(); cin >> n; set<ll>s; for (ll i = 0; i < n;i++) { cin >> t; s.insert(t); } ll B = *s.begin(), A = *s.rbegin(); reduce(A, B); while (flag) { flag = false; check(A,B,s, flag); } cout << A << "/" << B << endl; return 0; }
