顺序表与链表

顺序表与链表是非常基本的数据结构，它们可以被统称为线性表。

线性表（Linear List）是由 n（n≥0）个数据元素（结点）a[0]，a[1]，a[2]…，a[n-1] 组成的有限序列。

顺序表和链表，是线性表的不同存储结构。它们各自有不同的特点和适用范围。针对它们各自的缺点，也有很多改进的措施。

一、顺序表

顺序表一般表现为数组，使用一组地址连续的存储单元依次存储数据元素，如图 1 所示。它具有如下特点：

• 长度固定，必须在分配内存之前确定数组的长度。
• 存储空间连续，即允许元素的随机访问。
• 存储密度大，内存中存储的全部是数据元素。
• 要访问特定元素，可以使用索引访问，时间复杂度为 $O(1)$。
• 要想在顺序表中插入或删除一个元素，都涉及到之后所有元素的移动，因此时间复杂度为 $O(n)$。

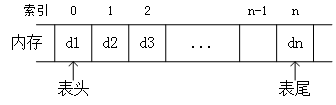
图 1 顺序表

顺序表最主要的问题就是要求长度是固定的，可以使用倍增-复制的办法来支持动态扩容，将顺序表变成“可变长度”的。

具体做法是初始情况使用一个初始容量（可以指定）的数组，当元素个数超过数组的长度时，就重新申请一个长度为原先二倍的数组，并将旧的数据复制过去，这样就可以有新的空间来存放元素了。这样，列表看起来就是可变长度的。

一个简单的实现如下所示，初始的容量为 4。

#include <string.h>

struct sqlist {
	int *items, size, capacity;
	sqlist():size(0), capacity(4) {
		// initial capacity = 4
		items = new int[capacity];
	}
	void doubleCapacity() {
		capacity *= 2;
		int* newItems = new int[capacity];
		memcpy(newItems, items, sizeof(int)*size);
		delete[] items;
		items = newItems;
	}
	void add(int value) {
		if (size >= capacity) {
			doubleCapacity();
		}
		items[size++] = value;
	}
};

这个办法不可避免的会浪费一些内存，因为数组的容量总是倍增的。而且每次扩容的时候，都需要将旧的数据全部复制一份，肯定会影响效率。不过实际上，这样做还是直接使用链表的效率要高，具体原因会在下一节进行分析。

二、链表

链表，类似它的名字，表中的每个节点都保存有指向下一个节点的指针，所有节点串成一条链。根据指针的不同，还有单链表、双链表和循环链表的区分，如图 2 所示。

图 2 链表

单链表是只包含指向下一个节点的指针，只能单向遍历。

双链表即包含指向下一个节点的指针，也包含指向前一个节点的指针，因此可以双向遍历。

循环单链表则是将尾节点与首节点链接起来，形成了一个环状结构，在某些情况下会非常有用。

还有循环双链表，与循环单链表类似，这里就不再赘述。

由于链表是使用指针将节点连起来，因此无需使用连续的空间，它具有以下特点：

• 长度不固定，可以任意增删。
• 存储空间不连续，数据元素之间使用指针相连，每个数据元素只能访问周围的一个元素（根据单链表还是双链表有所不同）。
• 存储密度小，因为每个数据元素，都需要额外存储一个指向下一元素的指针（双链表则需要两个指针）。
• 要访问特定元素，只能从链表头开始，遍历到该元素，时间复杂度为 $O(n)$。
• 在特定的数据元素之后插入或删除元素，不涉及到其他元素的移动，因此时间复杂度为 $O(1)$。双链表还允许在特定的数据元素之前插入或删除元素。

在上一节说到，利用倍增-复制的办法，同样可以让顺序表长度可变，而且效率比链表还要好，下面就简单的实现一个单链表来验证这一点，至于元素插入的顺序就不要在意了。

#include <stdio.h>
#include <time.h>
 
struct node {
	int value;
	node *next;
};
struct llist {
	node *head;
	void add(int value) {
		node *newNode = new node();
		newNode->value = value;
		newNode->next = head;
		head = newNode;
	}
};

int main() {
	int size = 100000;
	sqlist list1;
	llist list2;
	long start = clock();
	for (int i = 0;i < size;i++) {
		list1.add(i);
	}
	long end = clock();
	printf("sequence list: %d\n", end - start);
	start = clock();
	for (int i = 0;i < size;i++) {
		list2.add(i);
	}
	end = clock();
	printf("linked list: %d\n", end - start);
	return 0;
}

在我的电脑上，链表的耗时大约是顺序表的 4~8 倍。会这样，是因为数组只需要很少的几次大块内存分配，而链表则需要很多次小块内存分配，内存分配操作相对是比较慢的，因而大大拖慢了链表的速度。这也是为什么会出现内存池。

因此，链表并不像理论分析的那样美好，在实际应用中要受很多条件制约，一般情况下还是安心用顺序表的好。

三、静态链表

为了弥补链表在内存分配上的不足，出现了静态链表这么一个折中的办法。静态链表比较类似于内存池，它会预先分配一个足够长的数组，之后链表节点都会保存在这个数组里，这样就不需要频繁的进行内存分配了。

当然，这个方法的缺点是需要预先分配一个足够长的数组，肯定会导致内存的浪费。数组不够长到不是什么大不了的，使用第一节的动态扩容方法就是了。

静态链表一般是由两个链表组成，一个保存数据的链表，一个空闲节点的链表，如图 3 所示。

图 3 静态链表

当需要向链表中添加节点时，就从空闲链表中摘下一个使用。从链表中删除节点时，就将被删除的节点归还到空闲链表中。

在实现上，由于静态链表的节点都是存储在数组中的，所以经常使用数组索引代替指针，如果数组扩容了，也不会影响现有的节点。下面简单的实现了一个静态双向链表，没有添加动态扩容的能力。

struct snode {
	int value;
	int prev;
	int next;
};
struct sllist {
	snode *nodes;
	int head, freeHead;
	sllist():head(-1), freeHead(0) {
		// 初始化空闲链表，静态分配长度为 100。
		nodes = new snode[100];
		for (int i = 0;i < 100;i++) {
			nodes[i].next = i + 1;
		}
	}
	void add(int value) {
		// 从空闲链表中摘取节点。
		int newNode = freeHead;
		freeHead = nodes[freeHead].next;
		nodes[newNode].value = value;
		nodes[newNode].prev = -1;
		nodes[newNode].next = head;
		if (head != -1) {
			nodes[head].prev = newNode;
		}
		head = newNode;
	}
	void remove(snode node) {
		int idx = head;
		if (node.prev == -1) {
			head = node.next;
		} else {
			idx = nodes[node.prev].next;
			nodes[node.prev].next = node.next;
		}
		if (node.next != -1) {
			nodes[node.next].prev = node.prev;
		}
		// 将节点归还空闲链表。
		nodes[idx].next = freeHead;
		freeHead = idx;
	}
};

静态链表的效率几乎跟数组一样，极大的提升了链表的效率。不过因为链表的效率受内存分配影响，不同的语言可能有不同的表现，具体情况还需要实验分析才可以。

四、块状链表

块状链表则是链表和顺序表的结合体，将多个顺序表以链表连接起来，如图 4 所示。

图 4 块状链表

这种数据结构的优点是结合了顺序表和链表的优点，长度可变，而且插入、删除也比较迅速（不必移动全部元素，只需要移动某一个或几个块中的元素），时间复杂度约为 $O(\sqrt n)$，内存的占用也不会像链表那么多。

但是缺点也很明显，就是实现起来过于复杂，要想让时间复杂度达到 $O(\sqrt n)$，需要令块的个数和每块中存储的元素个数都接近 $\sqrt n$ 才行，这进一步限制了块状链表的应用。

STL 中的 deque 结构比较类似于块状链表，只不过它记录每一块使用的仍然是数组，而不是链表。同时 deque 只允许在两端进行插入和删除，实现上就容易很多。

五、跳表

跳表是针对有序链表进行优化的一种数据结构。它通过为链表节点随机化的添加前进链接，得以快速的跳过部分列表，如图 5 所示。

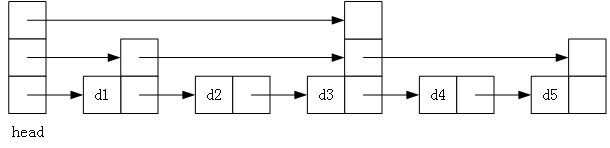
图 5 跳表

跳表会分为很多层，最底层就是普通的链表，高层则是用来快速获取后面的节点的。查找的时候，会从顶层的头节点开始向后查找，直到找到小于或等于目标的最后一个节点（链表是有序的，这是前提条件）。如果未能找到元素，则从下层链表接着找，最底层的普通链表保证一定能找到目标元素。

以上图为例，现在要查找元素 d4，那么首先会沿着顶层链表查找，找到 d3，接着沿着第二层链表查找，下一个元素是 d5 > d4，那么就只能沿着底层链表查找，成功找到元素 d4。动画演示可见图 6。

图 6 跳表查找过程

跳表的效率还是很高的，可以比拟二叉查找树（$O(\log n)$），而且实现起来比二叉查找树要简单一些，属于以空间换时间的数据结构（需要很多额外的链表指针）。

我目前也没有仔细阅读过跳表的论文（Pugh W. Skip lists: a probabilistic alternative to balanced trees[J]. Communications of the ACM, 1990, 33(6): 668-676.），所以不是很明白具体的实现，以上内容仅供参考，跳表的论文和代码可以从这里下载。