C# 词法分析器(三)正则表达式 update 2022.09.11
系列导航
- (一)词法分析介绍
- (二)输入缓冲和代码定位
- (三)正则表达式
- (四)构造 NFA
- (五)转换 DFA
- (六)构造词法分析器
- (七)总结
正则表达式是一种描述词素的重要表示方法。虽然正则表达式并不能表达出所有可能的模式(例如“由等数量的 a 和 b 组成的字符串”),但是它可以非常高效的描述处理词法单元时要用到的模式类型。
一、正则表达式的定义
正则表达式可以由较小的正则表达式按照规则递归地构建。每个正则表达式 $r$ 表示一个语言 $L(r)$,而语言可以认为是一个字符串的集合。正则表达式有以下两个基本要素:
- $\epsilon$ 是一个正则表达式, $L( \epsilon ) = { \epsilon }$,即该语言只包含空串(长度为 0 的字符串)。
- 如果 $a$ 是一个字符,那么 $\bf{ a }$ 是一个正则表达式,并且 $L( \bf{a} ) = \{ a \}$,即该语言只包含一个长度为 $1$ 的字符串 $a$。
由小的正则表达式构造较大的正则表达式的步骤有以下四个部分。假定 $r$ 和 $s$ 都是正则表达式,分别表示语言 $L(r)$ 和 $L(s)$,那么:
- $(r)|(s)$ 是一个正则表达式,表示语言 $L(r) \cup L(s)$,即属于 $L(r)$ 的字符串和属于 $L(s)$ 的字符串的集合( $L(r) \cup L(s) = \left\{ {s|s \in L(r)\ or\ s \in L(s)} \right\}$)。
- $(r)(s)$ 是一个正则表达式,表示语言 $L(r)L(s)$,即从 $L(r)$ 中任取一个字符串,再从 $L(s)$ 中任取一个字符串,然后将它们连接后得到的所有字符串的集合( $L(r)L(s) = \left\{ {st|s \in L(r)\ and\ t \in L(s)} \right\}$)。
- $(r)*$ 是一个正则表达式,表示语言 $L(r)*$,即将 $L(r)$ 连接 $0$ 次或多次后得到的语言。
- $(r)$ 是一个正则表达式,表示语言 $L(r)$。
上面这些规则都是由 Kleene 在 20 世纪 50 年代提出的,在之后有出现了很多针对正则表达式的扩展,他们被用来增强正则表达式表述字符串模式的能力。这里采用是类似 Flex 的正则表达式扩展,风格则类似于 .Net 内置的正则表达式:
| 正则表达式 | 描述 | ||||||||||||||||||||||
| x | 单个字符 x。 | ||||||||||||||||||||||
| . | 除了换行以外的任意单个字符。 | ||||||||||||||||||||||
| [xyz] | 一个字符类,表示 'x','y','z' 中的任意一个字符。 | ||||||||||||||||||||||
| [a-z] | 一个字符类,表示 'a' 到 'z' 之间的任意一个字符(包含 'a' 和 'z')。 | ||||||||||||||||||||||
| [^a-z] | 一个字符类,表示除了 [a-z] 之外的任意一个字符。 | ||||||||||||||||||||||
| [a-z-[b-f]] | 一个字符类,表示 [a-z] 范围减去 [b-f] 范围的字符,等价于 [ag-z]。 | ||||||||||||||||||||||
| r* | 将任意正则表达式 r 重复 0 次或多次。 | ||||||||||||||||||||||
| r+ | 将 r 重复 1 次或多次。 | ||||||||||||||||||||||
| r? | 将 r 重复 0 次或 1 次,即“可选”的 r。 | ||||||||||||||||||||||
| r{m,n} | 将 r 重复 m 次至 n 次(包含 m 和 n)。 | ||||||||||||||||||||||
| r{m,} | 将 r 重复 m 次或多次(大于等于 m 次)。 | ||||||||||||||||||||||
| r{m} | 将 r 重复恰好 m 次。 | ||||||||||||||||||||||
| {name} | 展开预先定义的正则表达式 “name”,可以通过预先定义一些正则表达式,以实现简化正则表达式。 | ||||||||||||||||||||||
| "[xyz]\"foo" | 原义字符串,表示字符串“[xyz]"foo”,用法与 C# 中定义字符串基本相同。 | ||||||||||||||||||||||
| \X | 表示 X 字符转义,如果 X 是 'a','b','t','r','v','f','n' 或 'e',表示相应的 ASCII 字符;如果 X 是 'w','W','s','S','d' 或 'D',则表示相应的字符类;否则表示字符 X。 | ||||||||||||||||||||||
| \nnn | 表示使用八进制形式指定的字符,nnn 最多由三位数字组成。 | ||||||||||||||||||||||
| \xnn | 表示使用十六进制形式指定的字符,nn 恰好由两位数字组成。 | ||||||||||||||||||||||
| \cX | 表示 X 指定的 ASCII 控制字符。 | ||||||||||||||||||||||
| \unnnn | 表示使用十六进制形式指定的 Unicode 字符,nnnn 恰好由四位数字组成。 | ||||||||||||||||||||||
| \p{name} | 表示 name 指定的 Unicode 通用类别或命名块中的单个字符。 | ||||||||||||||||||||||
| \P{name} | 表示除了 name 指定的 Unicode 通用类别或命名块之外的单个字符。 | ||||||||||||||||||||||
| (r) | 表示 r 本身。 | ||||||||||||||||||||||
| (?r-s:pattern) |
应用或禁用子正则表达式中指定的选项。选项可以是字符 'i','s' 或 'x'。 'i' 表示不区分大小写;'-i' 表示区分大小写。 以下下两列中的模式是等价的:
|
||||||||||||||||||||||
| (?#comment) | 表示注释,注释中不允许出现右括号 ')'。 | ||||||||||||||||||||||
| rs | r 与 s 的连接。 | ||||||||||||||||||||||
| r|s | r 与 s 的并。 | ||||||||||||||||||||||
| r/s | 仅当 r 后面跟着 s 时,才匹配 r。这里 '/' 表示向前看,s 并不会被匹配。 | ||||||||||||||||||||||
| ^r | 行首限定符,仅当 r 在一行的开头时才匹配。 | ||||||||||||||||||||||
| r$ | 行尾限定符,仅当 r 在一行的结尾时才匹配。这里的行尾可以是 '\n',也可以是 '\r\n'。 | ||||||||||||||||||||||
| <s>r | 仅当当前是上下文 s 时才匹配 r。 | ||||||||||||||||||||||
| <s1,s2>r | 仅当当前是上下文 s1 或 s2 时才匹配 r。 | ||||||||||||||||||||||
| <*>r | 在任意上下文中匹配 r。 | ||||||||||||||||||||||
| <<EOF>> | 表示在文件的结尾。 | ||||||||||||||||||||||
| <s1,s2><<EOF>> | 表示在上下文 s1 或 s2 时的文件的结尾。 |
这里与字符类和 Unicode 通用类别相关的知识请参考 C# 的正则表达式语言 - 快速参考中的“字符类”小节。大部分的正则表达式表示方法也与 C# 中的相同,有所不同的向前看(r/s)、上下文(<s>r)和文件结尾(<<EOF>>)会在之后的文章中解释。
利用上面的表格中列出扩展正则表达式,就可以比较方便的定义需要的模式了。不过有些需要注意的地方:
- 这里的定义不支持 POSIX Style 的字符类,例如 [:alnum:] 之类的,与 Flex 不同。
- $ 匹配行尾,即可以匹配 \n 也可以匹配 \r\n,也与 Flex 不同。
- 字符集的相减是 C# 风格的 [a-z-[b-f]],而不是 Flex 那样的 [a-c]{-}[b-z]。
- 向前看中的 \$ 只表示 '\$',而不再匹配行尾,例如 a/b\$ 仅当 "a" 后面是 "b\$" 时才匹配 "a"。
二、正则表达式的表示
虽然上面定义了正则表达式的规则,但它们表示起来却很简单,我使用 Cyjb.Compilers.RegularExpressions 命名空间下的 8 个类来表示任意的正则表达式,其类图如下所示:
图 1 正则表达式类图
其中,LexRegex 类是正则表达式的基类,CharClassExp 表示字符类(单个字符),LiteralExp 表示原义文本(多个字符组成的字符串),QuantifierExp 表示正则表达式重复(可以重复上限至下限之间的任意次数),AlternationExp 表示正则表达式的并(r|s),ConcatenationExp 表示正则表达式的连接(rs),AnchorExp 表示行首限定、行尾限定和向前看。
将 CharClassExp、LiteralExp、QuantifierExp、AlternationExp、ConcatenationExp 这些类进行嵌套,就可以表示大部分正则表达式了;AnchorExp 单独拿出来是因为它只能作为最外层的正则表达式,而不能位于其它正则表达式内部。这里并未考虑上下文,因为上下文的处理并不在正则表达式这里,而是在之后的“终结符符定义”部分。
正则表达式的表示比较简单,但为了更加易用,有必要提供从字符串(例如 "abc[0-9]+")转换为相应的正则表达式的转换方法。RegexCharClass 类是System.Text.RegularExpressions.RegexCharClass 类的包装,用于表示一个字符类,我对其中的某些函数进行了修改,以符合我这里的正则表达式定义。RegexParser 类则是用于正则表达式解析的类,具体的解析算法太过复杂,就不多加解释。
三、正则表达式
正则表达式构造好后,就需要使用它去匹配词素。一个词法分析器可能需要定义很多正则表达式,还可能包括上下文以及行首限定符,处理起来还是比较复杂的。为了简便起见,我会首先讨论怎么用一条正则表达式去匹配字符串,在之后的文章中再讨论如何用组合多条正则表达式去匹配词素。
使用正则表达式匹配字符串,一般都会用到有穷自动机(finite automata)的表示方法。有穷自动机是识别器(recognizer),只能对每个可能的输入回答“是”或“否”,表示时候与此自动机相匹配。或者说,不断的读入字符,直到有穷自动机回答“是”,此刻就正确的匹配了一个字符串。
有穷自动机分为两类:
- 不确定的有穷自动机(Nondeterministic Finite Automata,NFA)对其边上的标号没有任何限制。一个符号标记离开同一状态的多条边,并且空串 $\epsilon$ 也可以作为标号。
- 确定的有穷自动机(Deterministic Finite Automata,DFA)对于每个状态及自动机输入字母表中的每个符号有且只有一条离开该状态、以该符号为标号的边。
NFA 和 DFA 可以识别的语言集合是相同的(后面会说到 NFA 如何转换为等价的 DFA),并且这些语言的集合正好是能够用正则表达式描述的语言集合(正则表达式可以转换为等价的 NFA)。因此,采用有穷自动机来识别正则表达式描述的语言,也是很自然的。
3.1 不确定的有穷自动机 NFA
一个不确定的有穷自动机(NFA)由以下几个部分组成:
- 一个有穷的状态集合 $S$。
- 一个输入符号集合 $\Sigma$,即输入字母表(input alphabet)。我们假设空串 $\epsilon$ 不是 $\Sigma$ 中的元素。
- 一个转换函数(transition function),它为每个状态和 $\Sigma \cup \{ \epsilon \}$ 的每个符号都给出了相应的后继状态(next state)的集合。
- $S$ 中的一个状态 $s_0$ 被指定为开始状态,或者说初始状态。
- $S$ 的一个子集 $F$ 被指定为接受状态(或者说终止状态)的集合。
下图就是一个能识别正则表达式 (a|b)*baa 的语言的 NFA,边上的字母就是该边的标号。
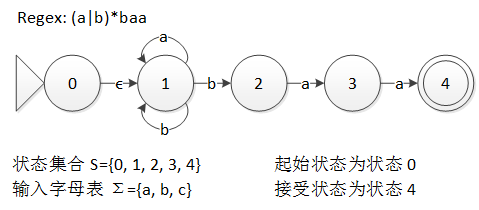
图 2 NFA 实例
NFA 的匹配过程很直观,从起始状态开始,每读入一个符号,NFA 就可以沿着这个符号对应的边前进到下一个状态($\epsilon$ 边不用读入符号也可以前进,当然也可以不前进),就这样不断读入符号,直到所有符号都读入进来,如果最后到达的是接受状态,那么匹配成功,否则匹配失败。
在状态 1 上,有两条标号为 b 的边,一条指向状态 1,一条指向状态 2,这就使自动机产生了不确定性——当到达状态 1 时,如果读入的字符是 'b',那么并不能确定应该转移到状态 1 还是 2,此时就需要使用集合保存所有可能的状态,把它们都尝试一遍才可以。
接下来尝试用这个 NFA 去匹配字符串 "ababaa"。
| 步骤 | 当前节点 | 读入字符 | 转移到节点 |
| 1 | {0, 1} | a | {1} |
| 2 | {1} | b | {1, 2} |
| 3 | {1, 2} | a | {1, 3} |
| 4 | {1, 3} | b | {1, 2} |
| 5 | {1, 2} | a | {1, 3} |
| 6 | {1, 3} | a | {1, 4} |
此时字符串已经全部读入,最后到达了状态 1 和 4,其中状态 4 是一个接受状态,因此 NFA 返回结果“是”。
使用 NFA 进行模式匹配的时间复杂度是 $O(k(n + m))$,其中 $k$ 为要匹配的字符串的长度,$n$ 为 NFA 中的状态数,$m$ 为 NFA 中的转移数。可见,NFA 的效率与输入字符串的长度和 NFA 的大小成正比,效率并不高。
3.2 确定的有穷自动机 DFA
确定的有穷自动机(DFA)是 NFA 的一个特例,其中:
- 没有输入 $\epsilon$ 之上的转换动作。
- 对每个状态 $s$ 和每个输入符号 $a$,有且只有一条标号为 $a$ 的边离开。
因此,NFA 抽象的表示了用来识别某个语言中串的算法,而相应的 DFA 则是具体的识别串的算法。
下图是同样识别正则表达式 (a|b)*baa 的语言的 DFA,看起来比 NFA 的要复杂不少。
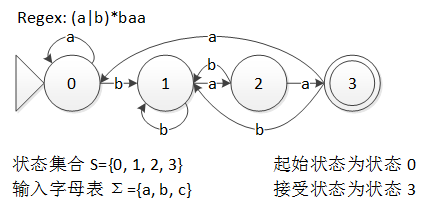
图 3 DFA 实例
DFA 的匹配过程则更加简单,因为没有了 $\epsilon$ 转换和不确定的转换,只要从起始状态开始,每读入一个符号,就直接沿着这个符号对应的边前进到下一个状态(这个状态是唯一的),就这样不断读入符号,直到所有符号都读入进来,如果最后到达的是接受状态,那么匹配成功,否则匹配失败。
接下来尝试用这个 DFA 去匹配字符串 "ababaa"。
| 步骤 | 当前节点 | 读入字符 | 转移到节点 |
| 1 | 0 | a | 0 |
| 2 | 0 | b | 1 |
| 3 | 1 | a | 2 |
| 4 | 2 | b | 1 |
| 5 | 1 | a | 2 |
| 6 | 2 | a | 3 |
此时字符串已经全部读入,最后到达了状态 3,是一个接受状态,因此 DFA 返回结果“是”。
使用 DFA 进行模式匹配的时间复杂度是 $O(k)$,其中 $k$ 为要匹配的字符串的长度,可见,DFA 的效率只与输入字符串的长度有关,效率非常高。
3.3 为什么使用 DFA
上面介绍的 NFA 和 DFA 识别语言的能力是相同的,但在词法分析中实际使用的都是 DFA,是有下面几种原因。
- NFA 的匹配效率比不过 DFA 的,词法分析器显然运行的越快越好。
- 虽然 DFA 的构造则要花费很长时间,一般是 $O(r^3)$,最坏情况下可能会是 $O(r^22^r)$,但在词法分析器这一特定领域中,DFA 只需要构造一次,就可以多次使用,而且 Flex 可以在生成源代码的时候就构造好 DFA,耗点时间也没有关系。
- DFA 在最坏情况下可能会使状态个数呈指数增长,《编译原理》上给出了一个例子 $(a|b)*a(a|b)^{n-1}$,识别这个正则表达式的 NFA 具有 $n+1$ 个状态,而 DFA 却至少有 $2^n$ 个状态,不过这么特殊的情况在编程语言中基本不会见到,不用担心这一点。
不过 NFA 还是有用的,因为 DFA 要利用 NFA,通过子集构造法得到;将正则表达式转换为 NFA,也有助于理解如何处理多条正则表达式和处理向前看。下一篇文章就开始介绍 NFA 的表示以及如何将正则表达式转换为 NFA。
相关代码都可以在这里找到。
作者:CYJB
出处:http://www.cnblogs.com/cyjb/
GitHub:https://github.com/CYJB/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号