C# 词法分析器(四)构造 NFA update 2022.09.11
系列导航
- (一)词法分析介绍
- (二)输入缓冲和代码定位
- (三)正则表达式
- (四)构造 NFA
- (五)转换 DFA
- (六)构造词法分析器
- (七)总结
有了上一节中得到的正则表达式,那么就可以用来构造 NFA 了。NFA 可以很容易的从正则表达式转换而来,也有助于理解正则表达式表示的模式。
一、NFA 的表示方法
在这里,一个 NFA 至少具有两个状态:首状态和尾状态,如图 1 所示,正则表达式 $t$ 对应的 NFA 是 N(t),它的首状态是 $H$,尾状态是 $T$。图中仅仅画出了首尾两个状态,其它的状态和状态间的转移都没有表示出来,这是因为在下面介绍的递归算法中,仅需要知道 NFA 的首尾状态,其它的信息并不需要关心。

图 1 NFA 的表示
我使用下面的 Nfa 类来表示一个 NFA,只包含状态列表和一个添加新状态的方法。
namespace Cyjb.Compilers.Lexers {
class Nfa : IList<NfaState> {
// NFA 状态列表。
List<NfaState> states
// 在当前 NFA 中创建一个新状态。
NfaState NewState() {}
}
}
NFA 的状态中,必要的属性只有三个:符号索引、状态转移和状态类型。只有接受状态的符号索引才有意义,它表示当前的接受状态对应的是哪个正则表达式,对于其它状态,都会被设为 -1。
状态转移表示如何从当前状态转移到下一状态,虽然 NFA 的定义中,每个节点都可能包含多个 $\epsilon$ 转移和多个字符转移(就是边上标有字符的转移)。但在这里,字符转移至多有一个,这是由之后给出的 NFA 构造算法的特点所决定的。
状态类型则是为了支持向前看符号而定义的,它可能是 Normal、TrailingHead 和 Trailing 三个枚举值之一,这个属性将在处理向前看符号的部分详细说明。
下面是 NfaState 类的定义:
namespace Cyjb.Compilers.Lexers {
class NfaState {
// 包含当前状态的 NFA。
Nfa Nfa;
// 当前状态的索引。
int Index;
// 当前状态关联到的符号。
int SymbolIndex;
// 当前状态的类型。
NfaStateType StateType;
// 字符类的转移对应的字符类集合。
ISet<CharClass> CharClassSet;
// 字符类转移的目标状态。
NfaState? CharClassTarget;
// ϵ 转移的集合。
IList<NfaState> EpsilonTransitions;
// 添加一个到特定状态的转移。
void Add(NfaState state, char ch);
// 添加一个到特定状态的转移。
void Add(NfaState state, CharSet chars);
// 添加一个到特定状态的ε转移。
void Add(NfaState state);
}
}
我在 NfaState 类中额外定义的两个属性 Nfa 和 Index 单纯是为了方便状态的使用。$\epsilon$ 转移直接被定义为一个列表,而字符转移则被定义为两个属性:CharClassTarget 和 CharClassTransition,CharClassTarget 表示目标状态,CharClassTransition 表示字符类,字符类会在下面详细解释。
NfaState 类中还定义了三个 Add 方法,分别是用来添加单个字符的转移、字符类的转移和 $\epsilon$ 转移的。
二、从正则表达式构造 NFA
这里使用的递归算法是 McMaughton-Yamada-Thompson 算法(或者叫做 Thompson 构造法),它比 Glushkov 构造法更加简单易懂。
2.1 基本规则
- 对于正则表达式 $\epsilon$,构造如图 2(a) 的 NFA。
- 对于包含单个字符 $a$ 的正则表达式 $\bf{a}$,构造如图 2(b) 的 NFA。

图 2 基本规则
上面的第一个基本规则在这里其实是用不到的,因为在正则表达式的定义中,并没有定义 $\epsilon$。第二个规则则用于转换表示字符类的正则表达式 CharClassExp,代码如下:
head.Add(tail, charClass.CharClass.GetCharSet());
2.2 归纳规则
有了上面的两个基本规则,下面介绍的归纳规则就可以构造出更复杂的 NFA。
假设正则表达式 $s$ 和 $t$ 的 NFA 分别为 $N(s)$ 和 $N(t)$。
1. 对于 $r=s|t$,构造如图 3 的 NFA,添加一个新的首状态 $H$ 和新的尾状态 $T$,然后从 $H$ 到 $N(s)$ 和 $N(t)$ 的首状态各有一个 $\epsilon$ 转移,从 $H$ 到 $N(s)$ 和 $N(t)$ 的尾状态各有一个 $\epsilon$ 转移到新的尾状态 $T$。很显然,到了 $H$ 后,可以选择是匹配 $N(s)$ 或者是 $N(t)$,并最终一定到达 $T$。

图 3 归纳规则 AlternationExp
这里必须要注意的是,$N(s)$ 和 $N(t)$ 中的状态不能够相互影响,也不能存在任何转移,否则可能会导致识别的结果不是预期的。
代码如下:
foreach (LexRegex subRegex in alternation.Expressions)
{
var (subHead, subTail) = BuildNFA(subRegex);
head.Add(subHead);
subTail.Add(tail);
}
2. 对于 $r=st$,构造如图 4 的 NFA,将 $N(s)$ 的首状态作为 $N(r)$ 的首状态,$N(t)$ 的尾状态作为 $N(r)$ 的尾状态,并在 $N(s)$ 的尾状态和 $N(t)$ 的首状态间添加一条 $\epsilon$ 转移。

图 4 归纳规则 ConcatenationExp
代码如下:
tail = head;
foreach (LexRegex subRegex in concatenation.Expressions)
{
var (subHead, subTail) = BuildNFA(subRegex);
tail.Add(subHead);
tail = subTail;
}
LiteralExp 也可以看成是多个 CharClassExp 连接而成,所以可以多次应用这个规则来构造相应的 NFA。
3. 对于 $r=s*$,构造如图 5 的 NFA,添加一个新的首状态 $H$ 和新的尾状态 $T$,然后添加四条 $\epsilon$ 转移。不过这里的正则表达式定义中,并没有显式定义 $r*$,因此下面给出 RepeatExp 对应的规则。

图 5 归纳规则 s*
4. 对于 $r=s\{m,n\}$,构造如图 6 的 NFA,添加一个新的首状态 $H$ 和新的尾状态 $T$,然后创建 $n$ 个 $N(s)$ 并连接起来,并从第 $m - 1$ 个 $N(s)$ 开始,都添加一条尾状态到 $T$ 的 $\epsilon$ 转移(如果 $m=0$,就添加从 $H$ 到 $T$ 的 $\epsilon$ 转移)。这样就保证了至少会经过 $m$ 个 $N(s)$,至多会经过 $n$ 个 $N(s)$。

图 6 归纳规则 QuantifierExp
不过如果 $n = \infty$,就需要构造如图 7 的 NFA,这时只需要创建 $m$ 个 $N(s)$,并在最后一个 $N(s)$ 的首尾状态之间添加一个类似于 $s*$ 的 $\epsilon$ 转移,就可以实现无上限的匹配了。如果此时再有 $m=0$,情况就与 $s*$ 相同了。

图 7 归纳规则 QuantifierExp $n = \infty$
综合上面的两个规则,得到了构造方法:
NfaState lastHead = head;
// 如果没有上限,则需要特殊处理。
int times = quantifier.MaxTimes == int.MaxValue ? quantifier.MinTimes : quantifier.MaxTimes;
if (times == 0)
{
// 至少要构造一次。
times = 1;
}
for (int i = 0; i < times; i++)
{
var (subHead, subTail) = BuildNFA(quantifier.InnerExpression);
lastHead.Add(subHead);
if (i >= quantifier.MinTimes)
{
// 添加到最终的尾状态的转移。
lastHead.Add(tail);
}
lastHead = subTail;
}
// 为最后一个节点添加转移。
lastHead.Add(tail);
// 无上限的情况。
if (quantifier.MaxTimes == int.MaxValue)
{
// 在尾部添加一个无限循环。
tail.Add(head);
}
5. 对于 $r=s/t$ 这种向前看符号,情况要特殊一些,这里仅仅是将 $N(s)$ 和 $N(t)$ 连接起来(同规则 2)。因为匹配向前看符号时,如果 $t$ 匹配成功,那么需要进行回溯,来找到 $s$ 的结尾(这才是真正匹配的内容),所以需要将 $N(s)$ 的尾状态标记为 TrailingHead 类型,并将 $N(T)$ 的尾状态标记为 Trailing 类型。标记之后的处理,会在下节转换为 DFA 时说明。
2.3 正则表达式构造 NFA 的示例
这里给出一个例子,来直观的看到一个正则表达式 (a|b)*baa 是如何构造出对应的 NFA 的,下面详细的列出了每一个步骤。

图 8 正则表达式 (a|b)*baa 构造 NFA 示例
最后得到的 NFA 就如上图所示,总共需要 14 个状态,在 NFA 中可以很明显的区分出正则表达式的每个部分。这里构造的 NFA 并不是最简的,因此与上一节《C# 词法分析器(三)正则表达式》中的 NFA 不同。不过 NFA 只是为了构造 DFA 的必要存在,不用费工夫化简它。
三、划分字符类
现在虽然得到了 NFA,但这个 NFA 还是有些细节问题需要处理。例如,对于正则表达式 [a-z]z,构造得到的 NFA 应该是什么样的?因为一条转移只能对应一个字符,所以一个可能的情形如图 9 所示。
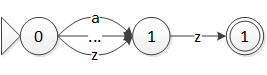
图 9 [a-z]z 构造的 NFA
前两个状态间总共需要 26 个转移,后两个状态间需要 1 个转移。如果正则表达式的字符范围再广些呢,比如 Unicode 范围?添加 6 万多条转移,显然无论是时间还是空间都是不能承受的。所以,就需要利用字符类来减少需要的转移个数。
字符类指的是字符的等价类,意思是一个字符类对应的所有字符,它们的状态转移完全是相同的。或者说,对自动机来说,完全没有必要区分一个字符类中的字符——因为它们总是指向相同的状态。
就像上面的正则表达式 [a-z]z 来说,字符 a-y 完全没有必要区分,因为它们总是指向相同的状态。而字符 z 需要单独拿出来作为一个字符类,因为在状态 1 和 2 之间的转移使得字符 z 和其它字符区分开来了。因此,现在就得到了两个字符类,第一个字符类对应字符 a-y,第二个字符类对应字符 z,现在得到的 NFA 如图 10 所示。

图 10 [a-z]z 使用字符类构造的 NFA
使用字符类之后,需要的转移个数一下就降到了 3 个,所以在处理比较大的字母表时,字符类是必须的,它即能加快处理速度,又能降低内存消耗。
而字符类的划分,就是将 Unicode 字符划分到不同的字符类中的过程。我目前采用的算法是一个在线算法,即每当添加一个新的转移时,就会检查当前的字符类,判断是否需要对现有字符类进行划分,同时得到转移对应的字符类。字符类的表示是使用一个 ISet<int>,因为一个转移可能对应于多个字符类。
初始:字符类只有一个,表示整个 Unicode 范围
输入:新添加的转移 $t$
输出:新添加的转移对应的字符类 $cc_t$
for each (每个现有的字符类 $CC$) {
$cc_1 = \left\{ c|c \in t\& c \in CC \right\}$
if ($cc_1= \emptyset$) { continue; }
$cc_2 = \left\{ c|c \in CC\& c \notin t \right\}$
将 $CC$ 划分为 $cc_1$ 和 $cc_2$
$cc_t = cc_1 \cup cc_t$
$t = \left\{ c|c \in t\& c \notin CC \right\}$
if ($t = \emptyset$) { break; }
}
这里需要注意的是,每当一个现有的字符类 $CC$ 被划分为两个子字符类 $cc_1$ 和 $cc_2$,之前的所有包含 $CC$ 的转移对应的字符类都需要更新为 $cc_1$ 和 $cc_2$,以包含新添加的子字符类。
我在 CharClassCollection 类中实现了该算法,其中充分利用了 CharSet 类集合操作效率高的特点。
HashSet<int> GetCharClass(string charClass) {
int cnt = charClassList.Count;
HashSet<int> result = new HashSet<int>();
CharSet set = GetCharClassSet(charClass);
if (set.Count == 0) {
// 不包含任何字符类。
return result;
}
CharSet setClone = new CharSet(set);
for (int i = 0; i < cnt && set.Count > 0; i++) {
CharSet cc = charClassList[i];
set.ExceptWith(cc);
if (set.Count == setClone.Count) {
// 当前字符类与 set 没有重叠。
continue;
}
// 得到当前字符类与 set 重叠的部分。
setClone.ExceptWith(set);
if (setClone.Count == cc.Count) {
// 完全被当前字符类包含,直接添加。
result.Add(i);
} else {
// 从当前的字符类中剔除被分割的部分。
cc.ExceptWith(setClone);
// 更新字符类。
int newCC = charClassList.Count;
result.Add(newCC);
charClassList.Add(setClone);
// 更新旧的字符类......
}
// 重新复制 set。
setClone = new CharSet(set);
}
return result;
}
四、多条正则表达式、限定符和上下文
通过上面的算法,已经可以实现将单个正则表达式转换为相应的 NFA 了,如果有多条正则表达式,也非常简单,只要如图 11 那样添加一个新的首节点,和多条到每个正则表达式的首状态的 $\epsilon$ 转移。最后得到的 NFA 具有一个起始状态和 $n$ 个接受状态。

图 11 多条正则表达式的 NFA
对于行尾限定符,可以直接看成预定义的向前看符号,r\$ 可以看成 r/\n 或 r/\r?\n(这样可以支持 Windows 换行和 Unix 换行),事实上也是这么做的。
对于行首限定符,仅当在行首时才会匹配这条正则表达式,可以考虑把这样的正则表达式单独拿出来——当从行首开始匹配时,就使用行首限定的正则表达式进行匹配;从其它位置开始匹配时,就使用其它的正则表达式进行匹配。
当然,即使是从行首开始匹配,非行首限定的正则表达式也是可以匹配的,所以就将所有正则表达式分为两个集合,一个包含所有的正则表达式,用于从行首匹配是使用;另一个只包含非行首限定的正则表达式,用于从其它位置开始匹配时使用。然后,再为这两个集合分别构造出相应的 NFA。
对于我的词法分析器,还会支持上下文。可以为每个正则表达式指定一个或多个上下文,这个正则表达式就会只在给定的上下文环境中生效。利用上下文机制,就可以更精细的控制字符串的匹配情况,还可能构造出更强大的词法分析器,例如可以在匹配字符串的同时处理字符串内的转义字符。
上下文的实现与上面行首限定符的思想相同,就是为将每个上下文对应的正则表达式分为一组,并分别构造 NFA。如果某个正则表达式属于多个上下文,就会将它复制并分到多个组中。
假设现在定义了 $N$ 个上下文,那么加上行首限定符,总共需要将正则表达式分为 $2N$ 个集合,并为每个集合分别构造 NFA。这样不可避免的会有一些内存浪费,但字符串匹配速度会非常快,而且可以通过压缩的办法一定程度上减少内存的浪费。如果通过为每个状态维护特定的信息来实现上下文和行首限定符的话,虽然 NFA 变小了,但存储每个状态的信息也会消耗额外的内存,在匹配时还会出现很多回溯的情况(回溯是性能杀手),效果可能并不好。
虽然需要构造 $2N$ 个 NFA,但其实只需要构造一个具有 $2N$ 个起始状态的 NFA 即可,每个起始状态对应于一个上下文的(非)行首限定正则表达式集合,这样做是为了保证这 $2N$ 个 NFA 使用的字符类是同一个,否则后面处理起来会非常麻烦。
现在,正则表达式对应的 NFA 就构造好了,下一篇文章中,我就会介绍如何将 NFA 转换为等价的 DFA。
相关代码都可以在这里找到。
作者:CYJB
出处:http://www.cnblogs.com/cyjb/
GitHub:https://github.com/CYJB/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。

